
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное произведение векторов.Содержание книги
Поиск на нашем сайте
Понятие векторного произведения вводится только для векторов в пространстве. Векторным произведением 1. 2. тройка векторов 3. длина вектора Геометрический смысл векторного произведения: длина вектора Свойства векторного произведения. 1) 2) l 3) 4) Если Следствия:
Если векторы
= СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. Понятие смешанного произведения определено только для векторов в пространстве. Смешанным произведением векторов Геометрический смысл смешанного произведения: модуль смешанного произведения Смешанное произведение векторов используется для проверки компланарности векторов: векторы Как вычислить смешанное произведение векторов
= ( = Следствие. Векторы
ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
ЗАДАЧА 1. РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ. Расстояние между точками M 1 (x 1, y 1, z 1) и M 2 (x 2, y 2, z 2) вычисляется как длина вектора Для точек на плоскости ЗАДАЧА 2. ДЕЛЕНИЕ ОТРЕЗКА В ОТНОШЕНИИ l. Даны точки M 1 (x 1, y 1, z 1) и M 2 (x 2, y 2, z 2). Найти координаты точки М (x, y, z), делящей отрезок М 1 М 2 в отношении l, если l = Если точка М лежит между точками М 1 и М 2, то отрезки l < 0. Поскольку для величин отрезков М 1 М = l М М 2, а векторы В координатной форме это равенство равносильно системе Если точка М делит отрезок М 1 М 2 пополам, то l = 1 и координаты точки М вычисляются по формулам Для точек М 1, М 2 и М, расположенных на плоскости и имеющих по две координаты, полученные формулы имеют вид
ПРЯМАЯ НА ПЛОСКОСТИ ЛИНИИ НА ПЛОСКОСТИ. Линия на плоскости может быть задана уравнением от двух переменных F (x, y) = 0, которому удовлетворяют координаты каждой точки этой линии и не удовлетворяют координаты ни одной другой точки. Для нахождения точек пересечения двух линий надо найти решения системы уравнений этих линий. Линия на плоскости, а также в пространстве, может рассматриваться как траектория движения точки. В этом случае ее описывают системой параметрических уравнений
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.10.220 (0.007 с.) |

 ´
´ 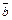 двух ненулевых векторов
двух ненулевых векторов  , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям: .
. ´
´ 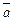 ´ l
´ l  ´
´  ¹
¹ 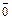 и
и  êê
êê 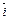 ´
´ 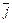 ´
´ 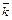 ´
´  ´
´ 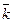 =
=  ;
; 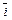 =
= 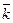 = –
= – 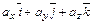 ,
,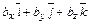 , то для вычисления векторного произведения
, то для вычисления векторного произведения 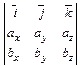 =
=  –
–  +
+ 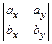 =
=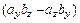 –
– 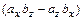 +
+  . Здесь использованы понятия определителей второго и третьего порядков, которые изучаются в теме «Линейная алгебра».
. Здесь использованы понятия определителей второго и третьего порядков, которые изучаются в теме «Линейная алгебра».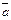 ,
, 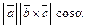 , где a — угол между вектором
, где a — угол между вектором  равно высоте параллелепипеда, взятой со знаком «+», если угол a острый, и со знаком «–», если угол a тупой. Длина вектора
равно высоте параллелепипеда, взятой со знаком «+», если угол a острый, и со знаком «–», если угол a тупой. Длина вектора 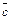 , который является основанием нашего параллелепипеда. В результате вышесказанного
, который является основанием нашего параллелепипеда. В результате вышесказанного 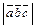 =
= 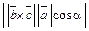 = S основания · h = V параллелепипеда. Если рассмотреть пирамиду, построенную на векторах
= S основания · h = V параллелепипеда. Если рассмотреть пирамиду, построенную на векторах  .
. компланарны Û
компланарны Û 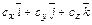 ?
?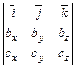 =
= =
=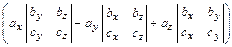 =
=  .
. . Поскольку вектор
. Поскольку вектор 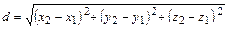 .
.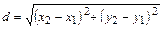 .
.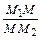 , где М 1 М и М М 2 величины направленных отрезков
, где М 1 М и М М 2 величины направленных отрезков 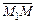 и
и 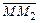 .
.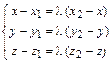 , которая имеет решение
, которая имеет решение 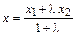 ,
,  ,
, 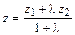 .
.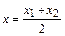 ,
, 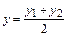 ,
, 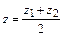 .
. .
.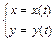 для линии на плоскости или
для линии на плоскости или 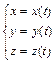 для линии в пространстве. При разных значениях параметра t получаем разные точки заданной линии. Можно использовать также векторное параметрическое уравнение линии:
для линии в пространстве. При разных значениях параметра t получаем разные точки заданной линии. Можно использовать также векторное параметрическое уравнение линии: 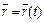 , где
, где  — радиус-вектор точки линии, определяемой значением параметра t.
— радиус-вектор точки линии, определяемой значением параметра t.


