
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие сходимости для применения итерационных методов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Итерационный процесс сходится, если сумма отношений модулей коэффициентов каждой строки к диагональному коэффициенту будет строго меньше единицы:
Неравенство будет справедливо, если диагональные элементы системы удовлетворяют условию:
Выбор начальных приближений не влияет на условие сходимости, поэтому можно полагать их равными нулю: (
Пример. Решить систему уравнений методом итераций с точностью
В системе первое уравнение имеет преобладающий коэффициент при неизвестном Переставив уравнения так, чтобы по диагонали стояли преобладающие элементы, получим:
Условия сходимости для коэффициентов преобразованной системы выполняются, т. к. Разрешив уравнения относительно неизвестных, запишем:
Выберем начальные приближения
Дальнейшие итерации дадут значения приближений:
Последнее приближение можно считать решением системы с точностью
Рис. 3.1 – Блок-схема. Метод простых итераций
Программа
procedure iteracii; var s,y: real; i,j: integer; bool: boolean; x: array[1..k] of real; t: array[1..k] of real; xn: array[1..k] of real; begin for i:=1 to k do begin x[i]:=b[i]; end; repeat for i:=1 to k do begin s:=0; for j:=1 to k do begin s:=s+a[i,j]*x[j] end; xn[i]:=(b[i]-s)/a[i,i]+x[i]; end; for i:=1 to k do begin t[i]:=abs(xn[i]-x[i]); x[i]:=xn[i]; end; bool:=true; i:=1; while (i<=k)and(bool=true) do begin if t[i]>=e then bool:=false; i:=i+1; end until bool=true; for i:=1 to k do begin writeln('X',i,'=',xn[i]); end; end;
3.2. Метод Зейделя
Этот метод является уточнённым методом итераций и носит название модифицированного метода итераций. Для вычисления приближения
Для составления блок-схемы алгоритма метода Зейделя воспользуемся формулой получения приближения на
где На каждом итерационном шаге будем вычислять погрешности
Рис. 3.2 – Блок-схема. Метод Зейделя
Программа
procedure zeydel; var s,y: real; i,j: integer; bool: boolean; x: array[1..k] of real; t: array[1..k] of real; xn: array[1..k] of real; begin writeln('Method zeydela: '); for i:=1 to k do begin x[i]:=b[i]; end; repeat for i:=1 to k do begin s:=0; for j:=1 to k do begin s:=s+a[i,j]*x[j]; end; xn[i]:=(b[i]-s)/a[i,i]+x[i]; t[i]:=abs(xn[i]-x[i]); x[i]:=xn[i]; end; bool:=true; i:=1; while (i<=k)and(bool=true) do begin if t[i]>=e then bool:=false; i:=i+1; end until bool=true; for i:=1 to k do begin writeln('X',i,'=',x[i]); end; end;
3.3. Метод Крамера
Алгоритм обладает высокой точностью, но не отличается относительно высокой скоростью, так как для решения системы из N уравнений требуется нахождение N + 1 детерминантов. В данной реализации алгоритма используется метод Гаусса для поиска детерминантов, что хуже, чем если бы метод Гаусса напрямую использовался для решения системы уравнений. Пусть дана система уравнений:
Если определитель матрицы
Рис. 3.3 – Блок-схема. Метод Крамера Программа
procedure kramer; var u,i: integer; opredel,opr,r: real; znak: integer; begin fillin; {Pivedenie k treugolnomu vidu} triangle(opr,znak); r:=1; for u:=1 to k do r:=r*matrix[u,u]; opredel:=r/opr*znak; if (opredel<>0) then begin for i:=1 to k do begin {perestanovka kolonki i} fillin; for u:=1 to k do begin if i<>1 then matrix[u,i-1]:=a[u,i-1]; matrix[u,i]:=b[u]; end; triangle(opr,znak); r:=1; for u:=1 to k do r:=r*matrix[u,u]; if (r<>0) then writeln('X',i,'= ',r/(opr*opredel)*znak) else writeln('X',i,'= ','Unknown'); end; end else writeln('Systema imeet mnojestvo resheniy.'); end; 3.4. Метод Гаусса
Данный метод решения СЛАУ является классичесиким. Он обладает высокой точностью и скоростью, так как основан на элементарных преобразованиях. Пусть имеется система уравнений:
Составим из этой системы матрицу:
Процесс решения состоит из двух этапов. На первом этапе (прямой ход) система с помощью элементарных преобразований над строками матрицы приводится к ступенчатому (треугольному) виду:
На втором этапе (обратный ход) последовательно находят переменные из получившейся ступенчатой матрицы. Принимая
Рис. 3.4 – Блок-схема. Метод Гаусса Программа
procedure gauss; var u,i: integer; tmp: real; {for compatability} begin fillin; {Pivedenie k treugolnomu vidu} triangle(tmp,i); {nahojdenie korney uravneniya} if (matrix[k,k]<>0) then begin smatrix[k]:=matrix[k,k+1]/matrix[k,k]; writeln('X',k,'= ',smatrix[k]); for u:=k-1 downto 1 do begin i:=u; while i<>k+1 do begin smatrix[u]:=smatrix[u]+smatrix[i]*matrix[u,i]; i:=i+1; end; smatrix[u]:=(matrix[u,k+1]-smatrix[u])/matrix[u,u]; writeln('X',u,'= ',smatrix[u]); end; end else writeln('Systema imeet mnojestvo resheniy'); end;
3.5. Дополнения к разделу 3.5.1. Комментарии
Реализация методов Крамера и Гаусса базируется на приведении матрицы к треугольному виду, поэтому данная процедура используется в обоих методах (подглавы 3.3 и 3.4). Также в реализации этих методов используется программа заполнения массива данными, которые представлены ниже. Они требуются для корректной работы методов. Точность этих методов, в отличие от итерационных, полностью базируется на точности математических операций, поэтому для повышения точности решения рекомендуется перейти на длинную математику (требуемая точность более
Рис. 3.5 – Блок-схема. Процедура приведения матрицы к треугольному виду Программа procedure triangle(var opr: real; var znak: integer); var u,i,j,w,y: integer; tmp,tmpz: real; begin opr:=1; znak:=1; for u:=1 to k-1 do begin for i:=1 to k-1 do {proverka kolonki na 0} begin j:=i; while (matrix[j,u]=0)and(matrix[j+1,u]<>0)and(j<>0) do begin y:=1; while (matrix[y,u]=0)and(y<>u) do begin y:=y+1; end; if (y=u) then begin znak:=znak*(-1); for w:=1 to k+1 do begin tmp:=matrix[j,w]; matrix[j,w]:=matrix[j+1,w]; matrix[j+1,w]:=tmp; end; end; j:=j-1; end; end; tmpz:=matrix[u,u]; {summirovanie strok} for j:=u+1 to k do begin tmp:=matrix[j,u]; opr:=opr*tmpz; for i:=u to k+1 do begin matrix[j,i]:=(-1)*tmp*matrix[u,i]+tmpz*matrix[j,i] end; end; end; end;
Входные данные: глобальный массив «matrix», объявленные переменные «opr» и «znak» (требуются для метода Крамера, подглава 3.3). Выходные данные: преобразованный глобальный массив «matrix».
Рис. 3.6 – Блок-схема. Процедура заполнения матрицы (подглавы 3.3, 3.4) Программа procedure fillin; var u,i: integer; begin for i:=1 to k+1 do begin for u:=1 to k do begin if i<>k+1 then matrix[u,i]:=a[u,i] else matrix[u,i]:=b[u]; end; end; end;
Входные данные: глобальный массив «matrix», массив коэффициентов линейных уравнений «a», массив свободных членов «b». Выходные данные: заполненный глобальный массив «matrix».
3.5.2. Пример работы программ
Все программы данного раздела представлены в виде процедур, для работы которых требуется ввод массива коэффициентов линейных уравнений «a», массива свободных членов «b», размерности данных массивов «b» (в раздел констант). Для итерационных методов в раздел констант следует добавить параметр точности «e». Так же потребуется объявить глобальные массивы «matrix» и «smatrix» (типа Real или точнее). Пусть требуется найти решение системы уравнений методом Гаусса:
Тогда упрощённая программа будет выглядеть следующим образом: Код программы: program SLAU; const k=4; a: array[1..k,1..k] of real=((5,0.8,-1.8,1), (2,-5,1,-2), (3,2,-8,2), (2,-4,5,-12)); b: array[1..k] of real=(0.4,-2,-2,6); var matrix: array[1..k,1..Succ(k)] of real; smatrix: array[1..k] of real; {Процедура заполнения матрицы } {Процедура приведения матрицы к треугольному виду} {Процедура метода Гаусса} begin gauss; readln; end. Вывод программы:
Стоит отметить, что решение систем линейных уравнений другими методами будет проходить аналогично, только необходимо произвести замену нужной процедуры в программе.
4. Численное решение обыкновенных
Рассмотрим задачу Коши. Найти решение обыкновенного дифференциального уравнения
4.1. Геометрическая интерпретация решения
Геометрический смысл решения обыкновенного дифференциального уравнения первого порядка методом Эйлера (методом Рунге-Кутта первого порядка) состоит в том, что на малом отрезке 4.2. Метод Эйлера
Приближённое значение в точке
Рис. 4.1 – Геометрическая интерпретация метода Эйлера Пример. Найти решение дифференциального уравнения Решение. При разбиении отрезка на 5 частей шаг постоянный В точке
Решение этой задачи будет тем точнее, чем меньше шаг деления отрезка
Рис. 4.2 – Блок-схема. Метод Эйлера
Программа
procedure eiler(x0,b,y0,n: real); var x,y: real; begin x:=x0; y:=y0; repeat writeln('X=',x,' ','Y=',y); x:=x+n; y:=y+n*f(x,y); until x>b; end;
4.3. Метод Рунге-Кутта (четвертого порядка)
Этот метод получил наиболее широкое распространение в практических расчетах. Его погрешность оценивается величиной
Здесь символом Замечание. Одним из недостатков метода является отсутствие простого способа оценки погрешности. Грубую оценку погрешности можно получить по формуле:
где
Если полученные результаты удовлетворяют допустимой погрешности, то в дальнейших расчетах шаг удваивают, иначе – уменьшают его вдвое. Приведенный способ приводит к необходимости дополнительных затрат времени счета на ПК.
Рис. 4.3 – Блок-схема. Метод Рунге-Кутта
Программа
procedure kutt(x0,b,y0,n: real); var x,y,dy,k1,k2,k3,k4,x1,x2,y1,y2,y3: real; begin x:=x0; y:=y0; repeat writeln('X=',x,' ','Y=',y); k1:=n*f(x,y); x1:=x+n/2; y1:=y+k1/2; k2:=n*f(x1,y1); y2:=y+k2/2; k3:=n*f(x1,y2); y3:=y+k3; x2:=x+n; k4:=n*f(x2,y3); dy:=(k1+2*k2+2*k3+k4)/6; y:=y+dy; x:=x+n; until x>b; end; 4.4. Дополнения к разделу 4.4.1. Комментарии
В разделе, представленном выше, описаны алгоритмы и программы, которые работают на заранее определенном отрезке
4.4.2. Пример работы программ
Все программы данного раздела представлены в виде процедур, для работы которых требуется ввод линейного дифференциального уравнений (в виде функции «f»), отрезка интегрирования Пусть требуется найти численное решение дифференциального уравнения
Программа
program diffur; {Уравнение} function f(x,y: real): real; begin f:=3*x+0.1*y; end; {Процедура метода Рунге-Кутта} Begin {x0,b – отрезок интегрирования; n – шаг; y0 – начальное условие. Вывод решения: kutt(x0,b,y0,n);} kutt(0,0.4,5,0.1); readln; end. Вывод программы:
Стоит отметить, что решение обыкновенных дифференциальных уравнений другими методами будет проходить так же, только необходимо произвести замену нужной процедуры в программе. Любая процедура раздела вызывается с 4 параметрами: x0,b – отрезок интегрирования; n – шаг; y0 – начальное условие.
5. Математическая обработка данных
На практике часто приходится иметь дело с данными, полученными в результате измерений, наблюдений. Они обычно представлены в виде табличных зависимостей Существует два подхода к решению поставленной задачи: а) функция должна точно проходить через узлы б) функция проходит с наименьшим отклонением от узлов и наиболее проста – аппроксимация.
5.1. Интерполяция
Задача интерполяции математически формулируется так: пусть на отрезке Требуется найти функцию
5.1.1. Локальная интерполяция
Локальная интерполяция заключается в том, чтобы использовать только близлежащие точки. Например, если значение
Рис. 5.1 – Блок-схема. Интерполяция Программа
procedure inlocal(v: real); var j: integer; begin for j:=1 to n-1 do begin if (v>x[j])and(v<x[j+1]) then break; end; writeln('X=',v,' Y=',y[j]+(y[j+1]-y[j])*(v-x[j])/(x[j+1]-x[j])); end;
5.1.2. Квадратичная интерполяция
Более точный результат можно получить, если использовать информацию о трех близлежащих точках (квадратичная интерполяция). В этом случае можно однозначно определить коэффициенты параболы Решение системы линейных уравнений вида:
позволяет определить неизвестные коэффициенты
Рис. 5.2 – Блок-схема. Квадратичная интерполяция Программа
procedure square(v: real); var a: array[1..3,1..3] of real; b: array[1..3] of real; i,j,kk: integer; aa,d,c,p,r,t,m1,m2,m3,m4: real; tmp: string; bool: boolean; begin i:=1; bool:=true; while (i<n+1)and(bool=true) do begin if v<x[i] then begin kk:=i-2; bool:=false; end; i:=i+1; end; if bool=false then begin for j:=1 to 3 do begin a[j,1]:=sqr(x[kk]); a[j,2]:=x[kk]; a[j,3]:=1; b[j]:=y[kk]; kk:=kk+1; end; m1:=a[2,1]*a[1,3]-a[1,1]*a[2,3]; m2:=a[1,2]*a[3,1]-a[3,2]*a[1,1]; m3:=a[2,1]*a[1,2]-a[1,1]*a[2,2]; m4:=a[1,3]*a[3,1]-a[3,3]*a[1,1]; p:=m3*m4-m1*m2; r:=a[3,1]*b[1]-a[1,1]*b[3]; t:=a[2,1]*b[1]-a[1,1]*b[2]; c:=(r*m3-t*m2)/p; d:=(t*m4-r*m1)/p; aa:=(b[1]-a[1,2]*d-a[1,3]*c)/a[1,1]; str(aa*v*v+d*v+c,tmp); end else tmp:='Chislo ne prin. posledovatelnoti..'; writeln('X=',v,' Y=',tmp); end; 5.1.3. Интерполяция Лагранжа
Более точное значение у может быть получено с помощью интерполяционных многочленов, использующих функции обо всех узлах фукции. В качестве примера приведем формулу интерполяционного многочлена Лагранжа:
Рис. 5.3 – Блок-схема. Интерполяция Лагранжа
Программа
procedure lagrange(v: real); var i,j: integer; yn,p1,p2: real; begin yn:=0; for i:=1 to n do begin p1:=1; p2:=1; for j:=1 to n do begin if j<>i then begin p1:=(v-x[j])*p1; p2:=(x[i]-x[j])*p2; end; end; yn:=yn+y[i]*p1/p2; end; writeln('X=',v,' Y=',yn); end;
5.1.4. Примеры
Для функции, заданной таблично найти значение
Решение. 1. Используя формулу локальной линейной интерполяции получим:
2. Для квадратичной зависимости составим систему линейных уравнений:
Решение этой системы дает значения Таким образом, 3. Многочлен Лагранжа выглядит следующим образом:
Стоит отметить, что последний результат наиболее точно соответствует данной зависимости. 5.2. Аппроксимация
Построение полного интерполяционного полинома требует определения его коэффициентов, число которых равно количеству заданных точек. При большом числе экспериментальных данных (
для нахождения коэффициентов которой используется следующий критерий: функционал должен принимать наименьшее значение (метод наименьших квадратов). Необходимым условием минимума указанного критерия является равенство нулю всех частных производных функции
5.2.1. Линейное приближение методом наименьших квадратов
Пусть аппроксимирующая функция является линейной относительно
В этом случае критерий принимает вид:
Условия минимума значения
решение которой позволяет определить неизвестные параметры Пример. Определить линейную зависимость для функции, заданной таблично:
Решение. Для определения неизвестных параметров функции
Решение данной системы позволяет найти значения
5.2.2. Аппроксимация полиномом
Пусть искомая функция является полиномом:
и условия минимума значения
Решение данной системы позволяет найти неизвестные коэффициенты
Рис. 5.3 – Блок-схема. Аппроксимация полиномом
Программа
procedure aproxym(v: real); var i,j,stp: integer; tmp: double; begin for i:=1 to k do begin stp:=i-1; for j:=succ(k)downto 1 do begin if j=k+1 then matrix[i,j]:=sumstep(0,n,i) else begin if (j=k)and(i=1) then matrix[i,j]:=n+1 else matrix[i,j]:=sumstep(stp,n,0); stp:=stp+1; end; end; end; gauss; tmp:=0; for i:=1 to k do begin tmp:=tmp+smatrix[i]*exp((k-i)*ln(v)); smatrix[i]:=0; end; writeln('X=',v,' Y=',tmp); end;
5.3. Дополнения к разделу 5.3.1. Комментарии
Точность интерполяции напрямую зависит от количества входных данных. Чем больше известных значений функции, тем более точно можно её интерполировать. По алгоритму представленному в подразделе 5.2.3, функция может быть аппроксимирована полиномом до 10 степени (определяется глобальной константой « Процедура «gauss», в программе подраздела 5.2.3 находит решение системы уравнений, полученных из матрицы «matrix» (алгоритм представлен в подразделе 3.4). После выполнения данной процедуры в массиве «smatrix» находятся решения данной системы уравнений. Также можно воспользоваться другими процедурами нахождения корней уравнения, но алгоритм подраздела 5.2.3 будет работать только тогда, когда решения будут находиться в матрице «smatrix».
Рис. 5.4 – Блок-схема. Функция суммирования
Программа
function sumstep(j,i,p: integer): real; var t: integer; tmp: double; begin tmp:=0; for t:=1 to i do begin if p=0 then tmp:=tmp+exp(j*ln(x[t])) else tmp:=tmp+y[t]*exp((p-1)*ln(x[t])); end; sumstep:=tmp; end;
5.3.2. Пример работы программ
Все программы данного раздела представлены в виде процедур, для работы которых требуется ввод значений аргумента функции, наличие массивов значений Пусть требуется найти значение функции в точках
Тогда упрощённая программа будет выглядеть следующим образом: Код программы program APROX; const n=6;{размерность массива значений функции} k=5;{степень полинома+1} x: array[1..n] of real=(1,2,3,4,5,6); y: array[1..n] of real=(8,21,58,161,396,853); var matrix: array[1..k,1..succ(k)] of real; smatrix: array[1..k] of real; {Процедура приведения матрицы к треугольному виду} {Процедура метода Гаусса} {Функция суммирования x^k} {Процедура аппроксимации полиномом} begin aproxym(1.676); aproxym(5.137); readln; end.
Вывод программы:
Коэффициенты полинома:
Важное замечание: из процедуры «gauss» убран вызов функции заполнения матрицы «fillin», так как матрица заполняется самим алгоритмом «aproxy». Если требуется решить задачу, представленную выше, с помощью интерполяции Лагранжа, то упрощённая программа будет выглядеть следующим образом: Программа program Interp; const n=6;{размерность массива значений функции} x: array[1..n] of real=(1,2,3,4,5,6); y: array[1..n] of real=(8,21,58,161,396,853); {Процедура метода Лагранжа} begin lagrange(1.676); lagrange(5.137); readln; end. Вывод программы:
Стоит отметить, что решение задачи другими методами будет проходить так же, только необходимо произвести замену нужной процедуры в программе. Любая процедура раздела вызывается с единственным параметром: v -значением аргумента (
Задания
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.87.151 (0.009 с.) |

 ,
,  .
. ,
,  ,
,  ) или отношениям свободных коэффициентов к диагональным коэффициентам: (
) или отношениям свободных коэффициентов к диагональным коэффициентам: ( ,
, 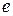 = 0.005.
= 0.005.
 , а второе – при
, а второе – при 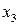 , а в третьем уравнении такого нет. Сложив первое и третье уравнение системы, можно получить преобладающий элемент при
, а в третьем уравнении такого нет. Сложив первое и третье уравнение системы, можно получить преобладающий элемент при  .
.
 ;
;  ;
;  .
.
 ;
;  ;
;  , тогда:
, тогда:
 ,
, ,
, .
. .
.
 используются приближения, полученные на предыдущем шаге
используются приближения, полученные на предыдущем шаге  ,
,  . Но к этому моменту уже найдены значения
. Но к этому моменту уже найдены значения  ,
,  ,…
,…  , поэтому для определения
, поэтому для определения 
 -м шаге в виде:
-м шаге в виде: ,
, и сравнивать их с заданной точностью
и сравнивать их с заданной точностью 


 .
. не равен нулю, то, поделив детерминант матрицы, полученной заменой столбца
не равен нулю, то, поделив детерминант матрицы, полученной заменой столбца  матрицы
матрицы  ), на детерминант самой матрицы
), на детерминант самой матрицы  .
.
 .
.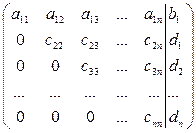 .
. , последовательно поднимаясь снизу вверх, подставляя уже найденные значения
, последовательно поднимаясь снизу вверх, подставляя уже найденные значения  , находят все решения системы.
, находят все решения системы.
 ).
).


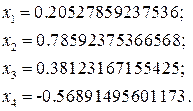
 , где
, где  ,
,  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . При численном решении поставленной задачи отрезок
. При численном решении поставленной задачи отрезок 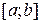 разбивают на
разбивают на  частей (не обязательно равных) и определяют приближенные значения искомой функции
частей (не обязательно равных) и определяют приближенные значения искомой функции  в точках деления
в точках деления  .
. интегральная кривая
интегральная кривая  дифференциального уравнения заменяется отрезком ее касательной в точке
дифференциального уравнения заменяется отрезком ее касательной в точке  .
. находится по формуле:
находится по формуле: .
.
 на отрезке [0;0.5] при начальном условии
на отрезке [0;0.5] при начальном условии  и числе разбиений
и числе разбиений  .
. . Начальное условие задачи
. Начальное условие задачи  ,
,  . Тогда при
. Тогда при  значение
значение  , т. е.
, т. е.  .
. значение
значение  . Продолжая вычисления по формуле Эйлера, получим:
. Продолжая вычисления по формуле Эйлера, получим:
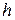 .
.
 , что дает возможность получить более точные результаты, чем в методе Эйлера. Не давая полного описания вывода формул, приведем их в следующем виде:
, что дает возможность получить более точные результаты, чем в методе Эйлера. Не давая полного описания вывода формул, приведем их в следующем виде:

 так же, как и в описанном методе Эйлера, обозначается правая часть решаемого дифференциального уравнения,
так же, как и в описанном методе Эйлера, обозначается правая часть решаемого дифференциального уравнения,  и
и  – приближённые значения интегральной функции соответственно в точках
– приближённые значения интегральной функции соответственно в точках  и
и 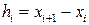 .
. ,
, – значение, вычисленное с шагом
– значение, вычисленное с шагом  – с шагом
– с шагом  .
.
 с заданным шагом
с заданным шагом  и начальными условиями
и начальными условиями  . Точность этих методов базируется на шаге интегрирования
. Точность этих методов базируется на шаге интегрирования  можно воспользоваться методом Рунге-Кутта более высокого порядка, чтобы уменьшить ошибку.
можно воспользоваться методом Рунге-Кутта более высокого порядка, чтобы уменьшить ошибку. , шага
, шага  .
. методом Рунге-Кутта на отрезке
методом Рунге-Кутта на отрезке  с шагом 0.1 и начальным условием
с шагом 0.1 и начальным условием  . Тогда упрощенная программа будет выглядеть следующим образом:
. Тогда упрощенная программа будет выглядеть следующим образом:
 , где
, где  , которая наиболее точно отражает зависимость результатов измерений. С её помощью можно найти значение для любой точки
, которая наиболее точно отражает зависимость результатов измерений. С её помощью можно найти значение для любой точки  – интерполяция;
– интерполяция; заданы точки
заданы точки  со своими значениями
со своими значениями  .
. . Решение этой задачи может быть выполнено двумя способами: локальной или полной интерполяцией.
. Решение этой задачи может быть выполнено двумя способами: локальной или полной интерполяцией. может быть найдено с помощью линейной интерполяции по формуле:
может быть найдено с помощью линейной интерполяции по формуле: .
.
 для любого отрезка
для любого отрезка  , которому принадлежит
, которому принадлежит 
 и значение
и значение 
 .
.
 в точке
в точке  методами локальной, линейной и квадратичной интерполяции, а также используя многочлен Лагранжа.
методами локальной, линейной и квадратичной интерполяции, а также используя многочлен Лагранжа. .
.
 ;
;  ;
;  .
. .
.
 ) хранение информации о коэффициентах так же затруднительно, как и хранение самих данных. В этих случаях ставится вопрос о нахождении функции
) хранение информации о коэффициентах так же затруднительно, как и хранение самих данных. В этих случаях ставится вопрос о нахождении функции  , зависящей от параметров, число которых значительно меньше количества заданных точек (
, зависящей от параметров, число которых значительно меньше количества заданных точек ( ). Аппроксимирующая функция часто ищется в виде полинома
). Аппроксимирующая функция часто ищется в виде полинома ,
,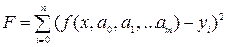
 по параметрам:
по параметрам:
 .
. .
. приводят к системе линейных уравнений:
приводят к системе линейных уравнений:
 и
и  .
.




 составим систему уравнений:
составим систему уравнений:
 ,
,  и указать линейную зависимость:
и указать линейную зависимость:  .
. приводят к системе
приводят к системе  линейных уравнений:
линейных уравнений:
 и определить функциональную зависимость. В частности, при m = 2 получится параболическая зависимость.
и определить функциональную зависимость. В частности, при m = 2 получится параболическая зависимость.
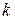 »). Далее требуются более точные арифметические операции, поэтому для аппроксимирования функции полиномом 10 степени и более требуется переход на длинную математику.
»). Далее требуются более точные арифметические операции, поэтому для аппроксимирования функции полиномом 10 степени и более требуется переход на длинную математику.
 из подраздела 5.2.3
из подраздела 5.2.3 и
и 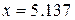 , представленной виде таблицы значений с помощью аппроксимации полиномом 4 степени:
, представленной виде таблицы значений с помощью аппроксимации полиномом 4 степени:

 ;
;  ;
;  ;
; ;
;  .
.



