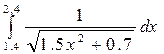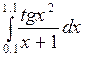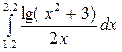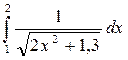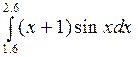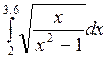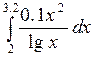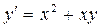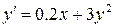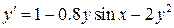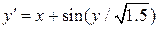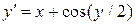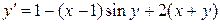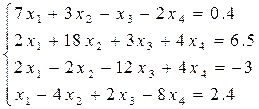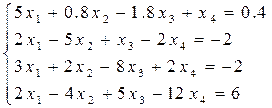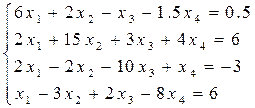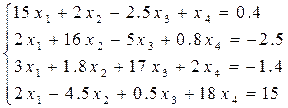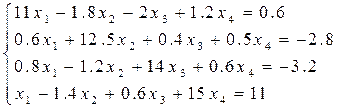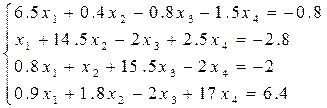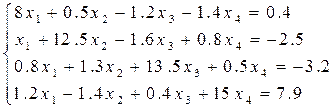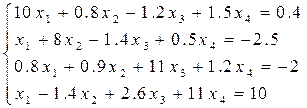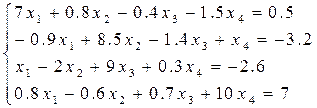Решение нелинейных уравнений

 

Решить нелинейное уравнение приближёнными методами. Варианты заданий представлены в таблице 6.1.

1. Отделить вещественные корни алгебраического уравнения аналитическим способом, используя понятие критических точек и формулу определения промежутка существования вещественных корней.

2. Вычислить все вещественные корни уравнения с точностью e = 10^-4 всеми методами (хорд, касательных, половинного деления, комбинированный - хорд и касательных.), используя приведённую программу.

 

Таблица 6.1 – Варианты заданий

Номер варианта	Уравнение
	x ^3 + 3 x ^2 1 = 0
	x ^3 3 x ^2 + 2.5 = 0
	2 x ^3 + 9 x ^2 10 = 0
	x ^3 12 x 5 = 0
	x ^3 3 x ^2 + 1.5 = 0
	2 x ^3 + 9 x ^2 4 = 0
	2 x ^3 3 x ^2 12 x + 8 = 0
	x ^3 6 x 8 = 0
	x ^3 + 3 x + 1 = 0
	x ^3 3 x ^2 + 6 x 2 = 0
	x ^3+ 3 x ^2 + 6 x 1 = 0
	x ^3 + 0.1 x ^2 + 0.4 x 1.2 = 0
	x ^3 3 x ^2 + 6 x 5 = 0
	2 x ^3 3 x ^2 12 x 5= 0
	x^3 – 3x + 3 = 0
	x ^3 + 3 x ^2 24 x 10 = 0
	2 x ^3 + 9 x ^2 21 = 0
	x ^3 + 3 x ^2 2 = 0
	x ^3 3 x ^2 24 x 3 = 0
	x ^3 + 3 x ^2 3.5 = 0
	x ^3 7 x 7 = 0
	x ^3 + 2 x 7 = 0
	x ^3 2 x ^2 6 = 0
	x ^3 2 x 5 = 0
	x ^3 2 x ^2 + 3 x 5 = 0
	x ^3 + 10 x 10 = 0
	2 x ^3 + 4 x ^2 1 = 0

Вычисление определённых интегралов

 

Используя программу, вычислить определённый интеграл с заданной точностью e = 10^-4 всеми указанными методами: прямоугольников, трапеций, Симпсона (варианты заданий представлены в таблице 6.2)..

 

Таблица 6.2 – Варианты заданий

Номер варианта	Уравнение

 

 

Окончание таблицы 6.2

 

Решение дифференциальных уравнений

Используя приведённую программу, найти решение дифференциального уравнения методами Эйлера и Рунге-Кутта четвёртого порядка на отрезке [0; 1] с шагом h = 0.1 (варианты заданий представлены в таблице 6.3)..

 

 

Таблица 6.3 – Варианты заданий

Номер варианта	Уравнение	Начальное условие
		y (0) = 0.2
		y (0) = 0.6
		y (0) = 0.3
		y (0) = 0.4
		y (0) = 0.4
		y (0) = 0.4
		y (0) = 0.7
		y (0) = 0.2
		y (0) = 0.4
		y (0) = 0.4
		y (0) = 0
		y (0) = 0
		y (0) = 0.8
		y (0) = 1.2
		y (0) = 1.4
		y (0) = 0
		y (0) = 0
		y (0) = 0.1
		y (0) = 0
		y (0) = 1
		y (0) = 0
		y (0) = 0
		y (0) = 0
		y (0) = 0
		y (0) = 0

Решение системы линейных уравнений

Решить систему линейных уравнений методом простых и уточнённых итераций – методом Зейделя с точностью e = 10^-5, используя программу (варианты заданий представлены в таблице 6.4). Предварительно проверить условие сходимости.

 

Таблица 6.4 – Варианты заданий

Номер варианта	Система

 

Продолжение таблицы 6.4

Продолжение таблицы 6.4

Окончание таблицы 6.4

 

Математическая обработка данных эксперимента моделирования

1. Получить функциональную зависимость по результатам экспериментов, используя интерполяцию и аппроксимацию функций.

2. Вычислить коэффициенты a, b, c, применяя метод наименьших квадратов для линейной и параболической зависимостей по результатам экспериментов (использовать данные, указанные в варианте).

3. Найти значения функции y для заданных аргументов x ₁ и x ₂ по полученной зависимости.

4. Сравнить значения функции y для заданных аргументов x ₁ и x ₂, полученные по методу наименьших квадратов и методу квадратичной интерполяции. Варианты заданий представлены в таблице 6.5.

Таблица 6.5 – Варианты заданий

	Номер варианта	Таблица данных
		X	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0
		Y	0.4	1.7	3.8	6.9	10.6	15.1	20.7	27.3
		X 1 = 1.235 X 2 = 3.871
		X	0.8	1.3	1.8	2.3	2.8	3.3	3.8	4.3
		Y	61.3	55.2	49.8	45.1	41.3	38.3	36.0	34.6
		X 1 = 2.529 X 2 = 3.982
		X	2.3	2.8	3.3	3.8	4.3	4.8	5.3	5.8
		Y	56.7	55.3	53.0	50.0	46.2	41.5	36.1	30.0
		X 1 = 2.721 X 2 = 4.981
	X	0.4	0.9	1.4	1.9	2.4	2.9	3.4	3.9
	Y	40.0	33.9	28.5	23.8	20.0	17.0	14.7	13.3
	X 1 = 1.581 X 2 = 2.683
	X	1.6	2.1	2.6	3.1	3.6	4.1	4.6	5.1
	Y	49.3	47.9	45.6	42.6	38.8	34.1	28.7	22.6
	X 1 = 2.871 X 2 = 4.593
	X	2.2	2.7	3.2	3.7	4.2	4.7	5.2	5.7
	Y	41.5	40.1	37.8	34.8	31.0	26.3	20.9	14.8
	X 1 = 2.923 X 2 = 4.981
	X	0.3	0.8	1.3	1.8	2.3	2.8	3.3	3.8
	Y	55.2	49.1	43.7	39.0	35.2	32.2	29.9	28.5
	X 1 = 1.923 X 2 = 2.981
	X	1.9	2.4	2.9	3.4	3.9	4.4	4.9	5.4
	Y	55.4	54.0	51.7	48.7	44.9	40.2	34.8	28.7
	X 1 = 2.371 X 2 = 4.632
	X	1.2	1.7	2.2	2.7	3.2	3.7	4.2	4.7
	Y	36.6	35.2	32.9	29.9	26.1	21.4	16.0	9.9
	X 1 = 2.921 X 2 = 4.121

Продолжение таблицы 6.5

	X	2.0	2.5	3.0	3.5	4.0	4.5	5.0	5.5
	Y	60.1	54.0	48.6	43.9	40.1	37.1	34.8	33.4
	X 1 = 2.783 X 2 = 4.821
	X	1.8	2.3	2.8	3.3	3.8	4.3	4.8	5.3
	Y	58.2	56.8	54.5	51.5	47.7	43.0	37.6	31.5
	X 1 = 2.892 X 2 = 3.921
	X	0.7	1.2	1.7	2.2	2.7	3.2	3.7	4.2
	Y	38.5	32.4	27.0	22.3	18.5	15.5	13.2	11.8
	X 1 = 2.547 X 2 = 2.893
	X	2.4	2.9	3.4	3.9	4.4	4.9	5.4	5.9
	Y	52.9	51.5	49.2	46.2	42.4	37.7	32.3	26.2
	X 1 = 4.721 X 2 = 5.67
	X	0.2	0.7	1.2	1.7	2.2	2.7	3.2	3.7
	Y	43.8	37.7	32.3	27.6	23.8	20.8	18.5	17.1
	X 1 = 2.371 X 2 = 2.831
	X	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.5
	Y	40.9	39.5	37.2	34.2	30.4	25.7	20.3	14.2
	X 1 = 3.281 X 2 = 3.982
	X	2.9	3.4	3.9	4.4	4.9	5.4	5.9	6.4
	Y	55.8	49.7	44.3	39.6	35.8	32.8	30.5	29.7
	X 1 = 3.72 X 2 = 5.92
	X	2.6	3.1	3.6	4.1	4.6	5.1	5.6	6.1
	Y	45.1	43.7	41.4	38.4	34.6	29.9	24.5	18.4
	X 1 = 3.581 X 2 = 4.79
	X	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0
	Y	41.6	35.5	30.1	25.4	21.6	18.6	16.3	14.9
	X 1 = 1.879 X 2 = 2.37
	X	2.8	3.3	3.8	4.3	4.8	5.3	5.8	6.3
	Y	46.6	45.2	42.9	39.9	36.1	31.4	26.0	19.9
	X 1 = 3.92 X 2 = 5.47
	X	2.1	2.6	3.1	3.6	4.1	4.6	5.1	5.6
	Y	50.1	44.0	38.6	33.9	30.1	27.1	24.8	23.4
	X 1 = 4.87 X 2 = 2.69
	X	1.7	2.2	2.7	3.2	3.7	4.2	4.7	5.2
	Y	48.0	46.6	44.3	41.3	37.5	32.8	27.4	21.3
	X 1 = 3.87 X 2 = 4.29
	X	1.0	1.5	2.0	2.5	3.0	3.5	4.0	4.5
	Y	48.7	42.6	37.2	32.5	28.7	25.7	23.4	22.0
	X 1 = 2.894 X 2 = 4.2
	X	2.5	3.0	3.5	4.0	4.5	5.0	5.5	6.0
	Y	44.5	43.1	40.8	37.8	34.0	29.3	23.9	17.8
	X 1 = 3.4 X 2 = 2.5
	X	1.4	1.9	2.4	2.9	3.4	3.9	4.4	4.9
	Y	52.2	46.1	40.7	36.0	32.2	29.2	26.9	25.5
	X 1 = 2.47 X 2 = 3.72

Окончание таблицы 6.5

	X	0.1	0.6	1.1	1.6	2.1	2.6	3.1	3.6
	Y	49.7	48.3	46.0	43.0	39.2	34.5	29.1	23.0
	X 1 = 1.72 X 2 = 3.32
	X	2.7	3.2	3.7	4.2	4.7	5.2	5.7	6.2
	Y	47.0	40.9	35.5	30.8	27.0	24.0	21.7	20.3
	X 1 = 3.94 X 2 = 5.47
	X	1.3	1.8	2.3	2.8	3.3	3.8	4.3	4.8
	Y	42.4	41.0	38.7	35.7	31.9	27.2	21.8	15.7
	X 1 = 2.21 X 2 = 3.95

 

Библиографический список

 

 

1. Шоль Н. Р. Информатика: учеб. пособие / Н. Р.Шоль, Л. М.Лихачёва, В. Н.Лихачёв, О. Н. Туманова. – Ухта: УГТУ, 2000. – 156 с.: ил.

2. Туманова О. Н. Программирование в среде DELPHI (лабораторные работы): метод. указания / О. Н. Туманова. – Ухта: УГТУ, 2005. – 40 с.

3. Л.П. Бойченко. Численные методы и их компьютерная реализация: учебное пособие /Л.П. Бойченко, Н.М. Выборова, О.Н. Туманова. – Ухта: УГТУ, 2012. – 90 с.

 

 

 

Учебное издание

 

 

З.Х. Ягубов, Л. П. Бойченко, Н. М. Выборова, О. Н. Туманова

 

Математическое моделирование с помощью численных методов на персональных компьютерах

 

Учебное пособие

 

Редактор Л. А. Кокшарова

Технический редактор Л. П. Коровкина

 

План 2013 г., позиция __. Подписано в печать __.__.2013 г.

Компьютерный набор. Гарнитура Times New Roman.

Формат 60´84 1/16. Бумага офсетная. Печать трафаретная.

Усл. печ. л. 5,2. Уч.-изд. л. 4,7. Тираж 100 экз. Заказ №___.

 

Ухтинский государственный технический университет.

169300, Республика Коми, г. Ухта, ул. Первомайская, д. 13.

Типография УГТУ.

169300, Республика Коми, г. Ухта, ул. Октябрьская, д. 13.