
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
З.Х. Ягубов, Л. П. Бойченко, О. Н. ТумановаСодержание книги
Поиск на нашем сайте
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ухтинский государственный технический университет» (УГТУ)
З.Х. Ягубов, Л. П. Бойченко, О. Н. Туманова
МАТЕМАТИЧЕСКОЕ МОДЕЛИ РОВАНИЕ С ПОМОЩЬЮ ЧИСЛЕННЫХ МЕТОДОВ НА ПЕРСОНАЛЬНЫХ КОМПЬЮТЕРАХ Учебное пособие
Ухта 2013 УДК 674.023 Я 31
Ягубов З.Х. Математическое моделирование с помощью численных методов на персональных компьютерах [Текст]: учеб. пособие / З.Х.Ягубов, Л. П. Бойченко, О. Н. Туманова. – Ухта: УГТУ, 2012. – 92 с.
ISBN 978-5-88179-704-1
В данном учебном пособии рассматривается применение методов вычислительной математики (численных методов) для моделирования различных процессов в области энергетики. К наиболее часто используемых методов на практике инженерных и научно-технических расчётах относятся такие как: методы решения задач линейной алгебры и нелинейных уравнений; методы теории приближения функций; методы численного дифференцирования интегрирования; методы решения обыкновенных дифференциальных уравнений и способы: аппроксимации и интерполяции. Это учебное пособие может быть использовано при изучении различных объёмов курсов «Математические модели в расчётах на ЭВМ», «Математическое моделирование в технике», «Высшая математика», «Экономико-математические методы и модели», а также при проведении научных исследований магистрантами и аспиратнтами направления 140400.62 «Электроэнергетика и электротехника». Данное учебное пособие предназначено для магистрантов и аспирантов как дневного, так и заочного отделений технического университета по специальности «Электроэнергетика и электротехника», а также для слушателей факультетов повышения квалификации в области моделирования с использованием персональных компьютеров и компьютерных технологий.
Учебное пособие рекомендовано к изданию.
Рецензенты: © Ухтинский государственный технический университет, 2012 © Ягубов З.Х., Бойченко Л. П., Выборова Н. М., Туманова О. Н., 2013
ISBN 978-5-88179-704-1
Оглавление
Введение........................................................................................................... 5 Глава 1. Приближённое решение нелинейных уравнений............................ 7 1.1. Графический способ отделения корней............................................. 7 1.2. Аналитический способ отделения корней......................................... 9 1.3. Метод половинного деления............................................................ 10 1.4. Метод хорд....................................................................................... 12 1.5. Метод касательных........................................................................... 15 1.6. Комбинированный метод................................................................. 18 1.7. Метод итераций................................................................................ 21 1.8. Дополнения к разделу...................................................................... 25 1.8.1. Комментарии........................................................................... 25 1.8.2. Пример работы программ.................................................... 29 Глава 2. Приближённое вычисление определенных интегралов................ 32 2.1. Геометрическая интерпретация....................................................... 32 2.2. Метод прямоугольников.................................................................. 32 2.3. Метод трапеций................................................................................ 34 2.4. Метод Симпсона............................................................................... 36 2.5. Дополнения к разделу...................................................................... 39 2.5.1. Комментарии........................................................................... 39 2.5.2. Пример работы программ..................................................... 39 Глава 3. Решение систем линейных уравнений............................................ 41 3.1. Метод простых итераций................................................................. 41 3.2. Метод Зейделя.................................................................................. 46 3.3. Метод Крамера................................................................................. 48 3.4. Метод Гаусса.................................................................................... 51 3.5. Дополнения к разделу...................................................................... 53 3.5.1. Комментарии........................................................................... 53 3.5.2. Пример работы программ..................................................... 57 Глава 4. Численное решение обыкновенных дифференциальных 4.1. Геометрическая интерпретация решения........................................ 59 4.2. Метод Эйлера................................................................................... 59 4.3. Метод Рунге-Кутта (четвёртого порядка)....................................... 61 4.4. Дополнения к разделу...................................................................... 63 4.4.1. Комментарии........................................................................... 63 4.4.2. Пример работы программ..................................................... 63 Глава 5. Математическая обработка данных............................................... 65 5.1. Интерполяция................................................................................... 65 5.1.1. Локальная интерполяция........................................................ 65 5.1.2. Квадратичная интерполяция.................................................. 66 5.1.3. Интерполяция Лагранжа........................................................ 69 5.1.4. Примеры................................................................................. 70 5.2. Аппроксимация................................................................................ 71 5.2.1. Линейное приближение методом наименьших квадратов.... 71 5.2.2. Аппроксимация полиномом................................................... 72 5.3. Дополнения к разделу...................................................................... 74 5.3.1. Комментарии........................................................................... 74 5.3.2. Пример работы программ..................................................... 76 Глава 6. Задания............................................................................................ 78 6.1 Решение нелинейных уравнений....................................................... 78 6.2 Вычисление определённых интегралов............................................ 79 6.3 Решение дифференциальных уравнений.......................................... 81 6.4 Решение систем линейных уравнений.............................................. 82 6.5 Математическая обработка данных эксперимента моделирования 86 Библиографический список........................................................................... 89
Введение В современных условиях при моделировании энергетических процессов в нефте-газо-добывающей промышленности, используя вычислительную технику, требуется от инженеров знаний основ алгоритмизации, программирования, вычислительной математики и применения этих знаний к решению различных задач моделирования с целью оптимизации, прогнозирования как технологических, так и технико-экономических показателей. Постановка научно-технической задачи сводится к формулировке математической задачи моделирования, решение которой зачастую можно выполнить только с помощью методов вычислительной математики, в частности, численных методов. Численный метод решения задачи – это определенная последовательность операций над числами, т.е. представляет собой вычислительный алгоритм, язык которого – числа и арифметические действия. Такое свойство языка позволяет реализовать численные методы на персональных компьютерах, что делает их мощным и универсальным инструментом моделирования и исследования различных энергетических процессов в нефте-газо-добывающей промышленности. Моделирование и решение задач на персональных компьютерах представляет собой достаточно сложный процесс. Он включает в себя несколько этапов: постановку задачи, её математическое моделирование (т.е. математическое описание), выбор метода решения, разработку алгоритма модели, составление программ, отладку и решение задачи, уточнение математической модели и её эксплуатацию с целью оптимизации и управления энергетическими процессами. Разработка алгоритма решения задачи или алгоритмизация задачи является наиболее ёмким этапом, включающим в себя этап программирования. В процессе его выполнения устанавливается необходимая последовательность арифметических и логических действий, с помощью которых может быть использован выбранный численный метод. Современная вычислительная техника требует от инженеров знаний основ алгоритмизации, программирования, вычислительной техники математики и применения этих знаний к решению различных практических и научно-исследовательских задач. В пособии рассматриваются математическое моделирование с помощью методов вычислительной математики, значительное внимание уделяется особенностям реализации вычислительных алгоритмов на персональном компьютере. Имеется большое количество примеров и геометрических иллюстраций, направленных на понимание механизмов их реализации. Примеры программ рассматриваются на языке Паскаль. Пособие предназначено для магистрантов, аспирантов и слушателей факультетов повышения квалификации технических вузов, а также для инженеров и научных работников, применяющих вычислительные методы для моделирования различных процессов. С помощью математического моделирования постановка научно-технической задачи сводится к формулировке математической задачи, решение которой зачастую можно выполнить только методами вычислительной математики. Разработка алгоритма моделирования задачи или алгоритмизация её является первым этапом программирования. В процессе его выполнения устанавливается необходимая последовательность арифметических и логических действий, с помощью которых может быть реализован выбранный численный метод. В данном учебном пособии рассматриваются следующие постановки задач мамематического моделирования с помощью численных методов. 1. Постановка задачи численного решения нелинейных уравнений. Графический и аналитический способы отделения корней. Уточнение корней нелинейного уравнения методами: половинного деления, касательных, хорд, комбинированным хорд и касательных, методом итераций. Алгоритмы, расчётные схемы, блок-схемы и программы для компьютеров. 2. Численное интегрирование. Вычисление определенного интеграла методом прямоугольников, трапеций, парабол (Симпсона). Алгоритмы, графическая интерпретация, расчётные схемы, блок-схемы и программы для компьютеров. 3. Интегрирование обыкновенных дифференциальных уравнений. Методы Эйлера и Рунге-Кутта: суть методов, их графическая интепретация, алгоритмы, расчётные схемы, блок-схемы и программы для компьютеров. 4. Решение систем линейных уравнений точными методами: Гаусса с выбором ведущего элемента и Крамера – метода определителей. Изложена их суть, алгоритмы, расчётные схемы, блок-схемы и программы для компьютеров. Численные методы: метод итераций и уточнённый метод – метод Зейделя для решения систем линейных уравнений: суть методов, алгоритмы, условие сходимости, расчётные схемы, блок-схемы и программы для колмпьютеров. Приводится сравнительная характеристика точных и приближённых методов решения систем линейных уравнений. 5. Постановка задачи математической обработки данных с помощью интерполяции и аппроксимации. Вычисление коэффициентов зависимости вида y = ax + b методом наименьших квадратов. Настоящее пособие основывается на материале учебного пособия «Программирование и численные методы» авторов Лихачевой Л. М., Соколовой Е. С., Тумановой О. Н., Лихачева В. Н., Лабызновой Г. Г., Долгобородовой Н. В., Бойченко Л. П., изданного в 1994 году в Ухтинском индустриальном институте.
1. Приближённое решение нелинейных уравнений
Всякое уравнение с одним неизвестным имеет вид:
где Совокупность значений переменной Решение уравнения приближёнными методами состоит из двух этапов: 1. Этап. Отделение корней, т. е. нахождение интервала изоляции для каждого корня; 2. Этап. Уточнение корней до заданной точности. Для отделения корней применяются графический и аналитический способы. Часто бывает так, что приближённое значение корня известно из физических соображений.
1.1. Графический способ отделения корней
Этот способ отделения корней заключается в построении графика функции
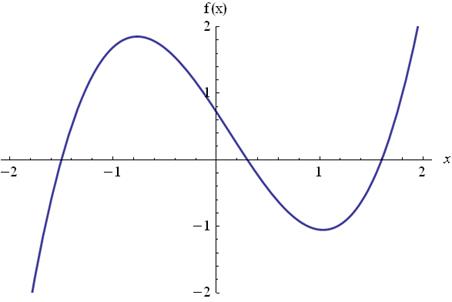
Примеры: Даны нелинейные уравнения: а) Построить график левой части уравнения (рис. 1):
Рис. 1.1 – График функции
Данное уравнение, как видно на графике, имеет три корня: x1, x2, x3. Это абсциссы пересечения графика; б) Построить график функций
Рис. 1.2 – Графики функций
Уравнение имеет один корень x1, который получен пересечением графиков функций:
1.2. Аналитический способ отделения корней
Этот способ для определения промежутков изоляции корней основан на теоремах, которые приводятся без доказательств. Теорема 1. Если функция Теорема 2. Если функция Пример: Найдем критические точки т. е. точки, в которых производная обращается в ноль: Составим таблицу знаков функции и производной:
Таким образом, как и в графическом методе, корни уравнения:
В случае алгебраического уравнения вида: Приведем не самый точный, но очень простой метод, который основывается на том, что все вещественные корни алгебраического уравнения с вещественными коэффициентами находятся в промежутке (-R; R),
где Пример. Отделить корни уравнения Решение. В этом уравнении R = 1+32/8 = 5 и корни уравнения лежат в промежутке (-5; 5). Критические точки данной функции могут быть найдены (что не всегда легко удается) из условия:
Здесь одна критическая точка Построим таблицу знаков функции и её производной:
Результаты анализа поведения функции показывают, что уравнение Уточнение корня состоит в определении значения корня, находящегося в заданном интервале, с определенной степенью точности. Приведем несколько методов, используемых для уточнения корней.
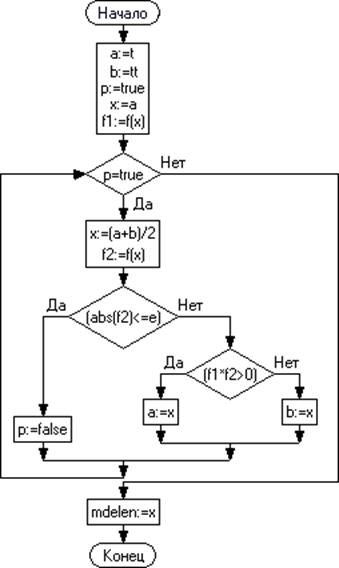
1.3. Метод половинного деления
Этот метод основан на делении отреза
На каждом этапе отрезок
Этот процесс деления отрезка пополам выполняется до тех пор, пока длина последнего отрезка не станет удовлетворять условию Пример. Найти корень уравнения Решение. Процесс вычисления проиллюстрирован ниже и приведён в таблице ниже:
Искомое значение корня находим по формуле:
Рис. 1.3 – Блок-схема. Метод половинного деления
Программа
function mdelen(t,tt,e: real): real; var x,a,b,f1,f2: real; p: boolean; begin a:=t; b:=tt; p:=true; x:=a; f1:=f(x); while p=true do begin x:=(a+b)/2; f2:=f(x); if (abs(f2)<=e) then begin p:=false; end else begin if (f1*f2>0) then a:=x else b:=x; end; end; mdelen:=x; end;
1.4. Метод хорд
Этот метод состоит в том, что на отрезке Здесь первая и вторая производная имеют разные знаки на отрезке
Рис. 1.4 – Первая и вторая производная имеют одинаковые знаки
Рис. 1.5 – Первая и вторая производная имеют разные знаки
Расчётные формулы: а) если
б) если
Итерационный процесс прекращается, как только
Рис. 1.6 – Блок-схема. Метод хорд Программа
function mhord(a,b,e: real): real; var x,x0,x1,ae: real; p: boolean; begin p:=true; x:=(a+b)/2; if (ff(x)*fff(x)>0) then begin x0:=a; ae:=b; end else begin x0:=b; ae:=a; end; while p=true do begin x1:=x0-f(x0)*(ae-x0)/(f(ae)-f(x0)); if (abs(x1-x0)<e) then p:=false else x0:=x1; end; mhord:=x1; end;
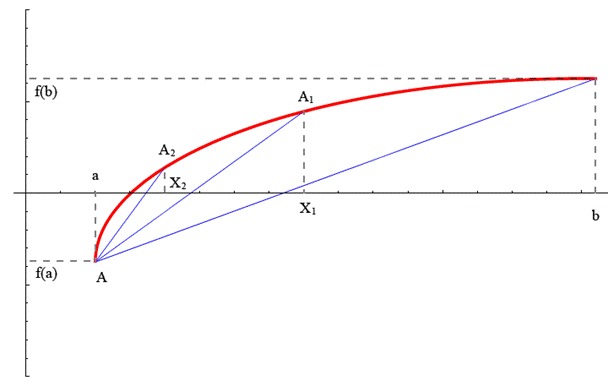
1.5. Метод касательных
Данный метод заключается в вычислении последовательных приближений к корню по формуле:
причём, За приближённое значение к корню принимается абсцисса точки пересечения касательной, проведенной к одной из точек дуги АВ, с осью ОХ. Процесс вычислений прекращается при выполнении условия
Рис. 1.7, а – Функция
Рис. 1.7, б – Функция
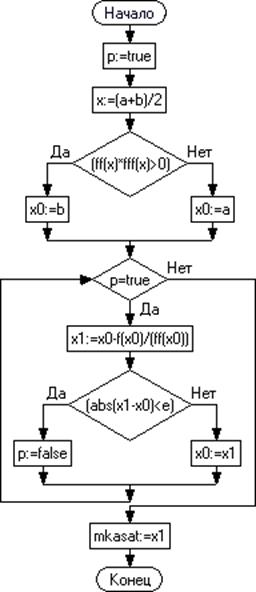
Рис. 1.8 – Блок-схема. Метод касательных
Программа
function mkasat(a,b,e: real): real; var x,x0,x1: real; p: boolean; begin p:=true; x:=(a+b)/2; if (ff(x)*fff(x)>0) then x0:=b else x0:=a; while p=true do begin x1:=x0-f(x0)/(ff(x0)); if (abs(x1-x0)<e) then p:=false else x0:=x1; end; mkasat:=x1; end;
1.6. Комбинированный метод
Этот метод состоит в объединении двух последних методов (хорд и касательных), описанных выше. Целесообразность его состоит в том, что для непрерывных функций Суть комбинированного метода изображена на рис. 1.6.
Рис. 1.9 – Случай возрастающей выпуклой вниз функции Расчётные формулы: а) Если
б) Если
Вычисления прекращаются при выполнении условия
Пример: Найти корень уравнения Решение. Корень уравнения отделен и находится на отрезке [1;2]. На левом конце отрезка производная данной функции равна нулю. Для выполнения расчётов следует сузить отрезок таким образом, чтобы в отрезке и на его концах производные функции были постоянного знака и не равны нулю. Возьмем отрезок [1.1; 2]. На концах отрезка функция принимает значения разных знаков, первая производная Это означает, что уравнение имеет один корень на отрезке [1.1; 2] и можно воспользоваться формулами (а) комбинированного метода:
Разность
Последние значения имеют разность меньше
Рис. 1.10 – Блок-схема. Комбинированный метод
Программа
function mcombo(t,tt,e: real): real; var x,a,b,a1,b1,r: real; p: boolean; begin a:=t; b:=tt; p:=true; while p=true do begin x:=(a+b)/2; if (ff(x)*fff(x)>0) then begin a1:=a-f(a)*(b-a)/(f(b)-f(a)); b1:=b-f(b)/ff(b); end else begin a1:=a-f(a)/ff(a); b1:=b-f(b)*(b-a)/(f(b)-f(a)); end; r:=abs(b1-a1); a:=a1; b:=b1; if (r<=2*e) then p:=false; end; x:=0; x:=(a+b)/2; mcombo:=x; end;
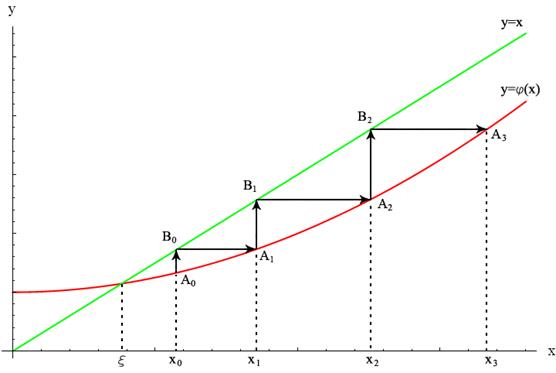
1.7. Метод итераций
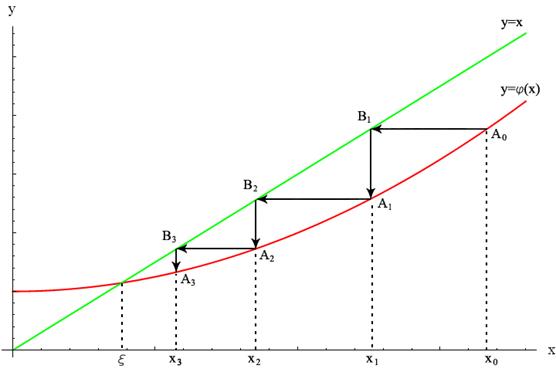
Этот метод заключается в том, что исходное уравнение вида Эта замена может быть выполнена по формуле: Данный метод последовательного приближения к корню заключается в том, что после выбора любого начального приближения к корню
Для вычислений второго и всех последующих приближений используется расчётная схема:
Таким же образом, строится последовательность следующих приближений
Последнее значение, полученное в результате вычислений, можно считать корнем уравнения Суть метода итераций изображена на рис. 1.11, а; 1.11, б и 1.11, в.
Рис. 1.11, a – Сходящийся итерационный процесс (
Рис. 1.11, б – Сходящийся итерационный процесс (
Рис. 1.11, в – Расходящийся итерационный процесс (
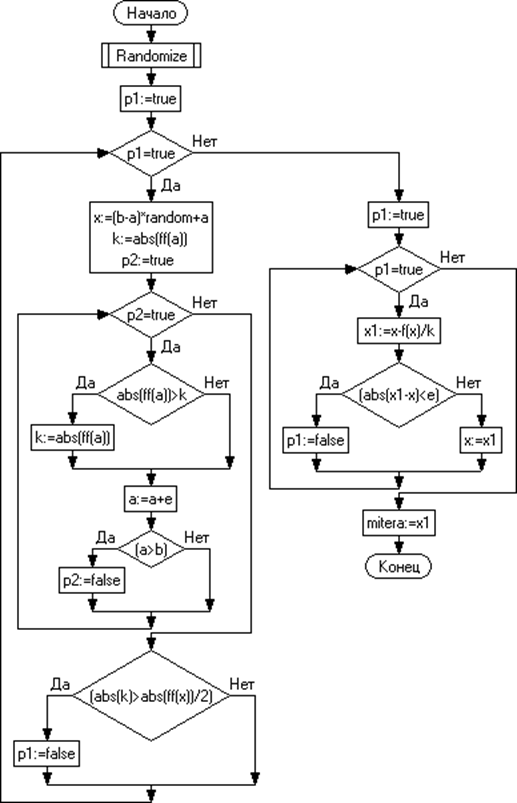
Рис. 1.12 – Блок-схема. Метод итераций
Программа
function mitera(a,b,e: real): real; var x,x1,k: real; p1,p2: boolean; begin Randomize; p1:=true; while p1=true do begin x:=(b-a)*random+a; k:=abs(ff(a)); p2:=true; while p2=true do begin if abs(ff(a))>k then k:=abs(ff(a)); a:=a+e; if (a>b) then p2:=false; end; if (abs(k)>abs(ff(x))/2) then p1:=false; end; p1:=true; while p1=true do begin x1:=x-f(x)/k; if (abs(x1-x)<e) then p1:=false else x:=x1; end; mitera:=x1; end;
1.8. Дополнения к разделу 1.8.1. Комментарии
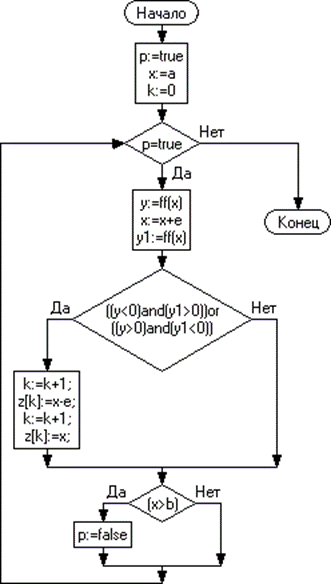
В разделе, представленном выше, описаны алгоритмы и программы, которые работают на заранее определённом отрезке Если же уравнение трансцендентное (не являющееся алгебраическим) или имеет достаточно большой разброс корней, то стоит прибегнуть к анализу функции. Многие методы в этой главе требуют численного дифференцирования. Соответственно точность этих методов будет базироваться не только на точности алгебраических операций. Если требуется большая вычислительная точность (погрешность менее Далее будут представлены две функции для нахождения первой и второй производных, а также процедура отделения корней полиномиального уравнения (рис. 1.13).
Рис. 1.13 – Блок-схема. Процедура нахождения промежутков Программа
procedure analytik(a,b,e: real); var x,y,y1: real; p: boolean; begin p:=true; x:=a; k:=0; while p=true do begin y:=f(x); x:=x+e; y1:=f(x); if ((y<0)and(y1>0))or((y>0)and(y1<0)) then begin k:=k+1; z[k]:=x-e; k:=k+1; z[k]:=x; end; if (x>b) then p:=false; end; end; Входные данные: предположительный промежуток существования корней ( Выходные данные: массив точек z[k], составляющих отрезки существования корней.
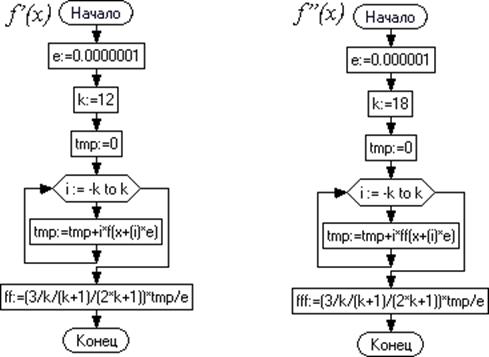
Рис. 1.14 – Блок-схема. Функции нахождения первой и второй производных Программа
function ff(x: extended): extended; var k,i: integer; e,tmp: extended; begin e:=0.0000001; k:=12; tmp:=0; for i:=-k to k do begin tmp:=tmp+i*f(x+(i)*e); end; ff:=(3/k/(k+1)/(2*k+1))*tmp/e; end; function fff(x: extended): extended; var k,i: integer; e,tmp: extended; begin e:=0.000001; k:=18; tmp:=0; for i:=-k to k do begin tmp:=tmp+i*ff(x+(i)*e); end; fff:=(3/k/(k+1)/(2*k+1))*tmp/e; end;
Функции основываются на формуле низко-шумного дифференциатора Ланцоша (ввиду простой реализации):
где
В любом случае для анализа функции требуется нахождение производных. В выражении, представленном выше, используется приближённая формула, дающая точность до Для достижения точности Ряды Тейлора требуют сложных преобразований, поэтому используют готовые формулы, полученные в ходе преобразований:
где
1.8.2. Пример работы программ
Все программы данного раздела представлены в виде функций (за исключением процедуры из пункта 1.8.3), для работы которых требуется ввод линейного уравнения (в виде функции «f»), промежутка существования корня Пусть требуется найти корень уравнения Тогда упрощённая програм
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.202.60 (0.012 с.) |

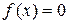 или
или 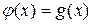 ,
,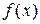 ,
, 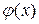 ,
, 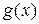 – заданные функции, определённые на некотором числовом множестве
– заданные функции, определённые на некотором числовом множестве 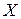 .
. .
.
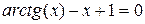 .
.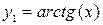 и
и 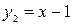 (рис. 1.2):
(рис. 1.2):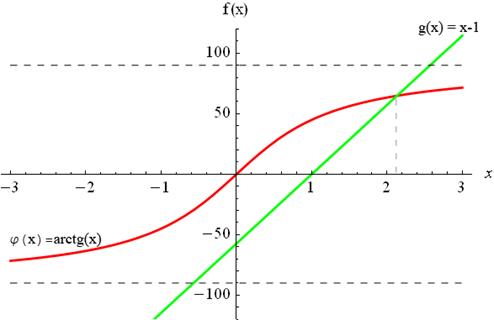
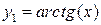 и
и 
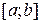 и принимает на концах этого отрезка значения разных знаков, то внутри отрезка
и принимает на концах этого отрезка значения разных знаков, то внутри отрезка  существует хотя бы один корень уравнения
существует хотя бы один корень уравнения  .
.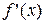 – знакопостоянна внутри отрезка, то существует единственный корень уравнения
– знакопостоянна внутри отрезка, то существует единственный корень уравнения 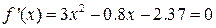 ;
; 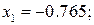
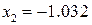 .
.


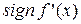


 ;
;  ;
; 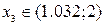 .
.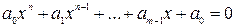 необходимо сначала определить промежутки существования всех корней, а затем применить аналитический метод.
необходимо сначала определить промежутки существования всех корней, а затем применить аналитический метод.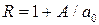 ,
,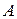 – наибольший по модулю коэффициент.
– наибольший по модулю коэффициент.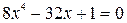 аналитическим способом.
аналитическим способом.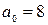 ,
,  , следовательно:
, следовательно: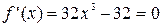 .
.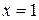 .
.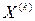 более близких к корню, по формуле:
более близких к корню, по формуле:

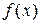 имеют разные знаки:
имеют разные знаки: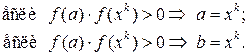
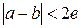 . Последнее означает, что
. Последнее означает, что  является корнем уравнения, вычисленным с точностью
является корнем уравнения, вычисленным с точностью 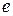 .
. методом половинного деления.
методом половинного деления.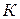
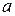
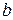
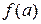
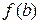
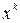
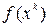

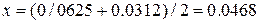 .
.
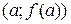 и
и 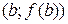 , а в качестве приближённого значения корня
, а в качестве приближённого значения корня 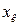 принимается значение абсциссы точки пересечения этой хорды с осью ОХ.
принимается значение абсциссы точки пересечения этой хорды с осью ОХ.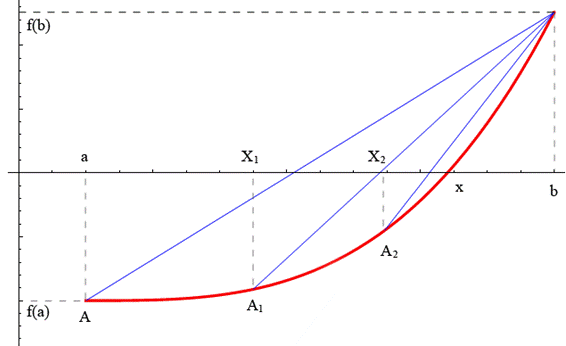
 на отрезке
на отрезке  ;
; на отрезке
на отрезке 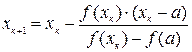 .
.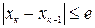 , а последнее значение
, а последнее значение 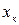 считается значением корня уравнения с точностью
считается значением корня уравнения с точностью 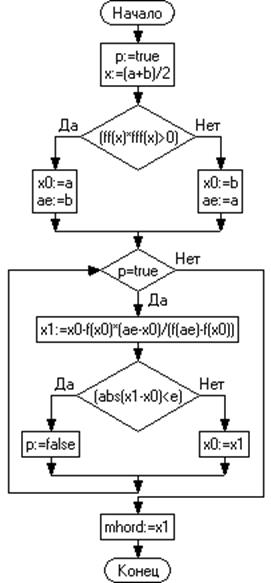
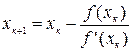 ,
,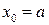 , если
, если  , если
, если 
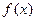 убывает на отрезке
убывает на отрезке 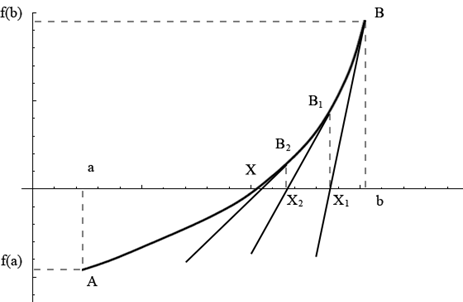

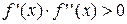 на отрезке
на отрезке 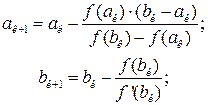
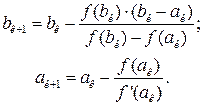
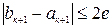 , а в качестве значения корня, полученного с точностью
, а в качестве значения корня, полученного с точностью  .
.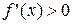 и
и  .
.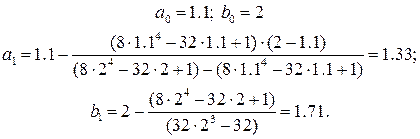
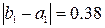 , что превышает заданную точность
, что превышает заданную точность 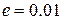 . Продолжая вычисления по формулам (а), получим:
. Продолжая вычисления по формулам (а), получим:
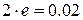 , и значение корня может быть принято равным:
, и значение корня может быть принято равным: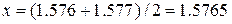 .
.
 таким образом, чтобы функция
таким образом, чтобы функция 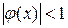 на отрезке
на отрезке 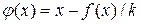 , где
, где 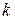 выбрано так, чтобы
выбрано так, чтобы 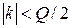 , где
, где  и знак
и знак  на отрезке
на отрезке 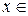
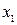 вычисляется путём подстановки
вычисляется путём подстановки 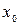 в правую часть преобразованного уравнения, т. е.
в правую часть преобразованного уравнения, т. е.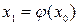 .
. .
.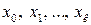 и процесс вычислений прекращается при выполнении условия:
и процесс вычислений прекращается при выполнении условия: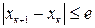 .
.
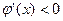 )
)
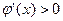 )
)
 состоит в поиске промежутка или промежутков существования корней. В случае полиномиального уравнения можно воспользоваться методом, представленным в подглаве 1.2.
состоит в поиске промежутка или промежутков существования корней. В случае полиномиального уравнения можно воспользоваться методом, представленным в подглаве 1.2.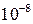 ), то следует перейти в алгоритмах от типа real к типу double (или Extended) или полностью перевести все арифметические действия на длинную математику (погрешность
), то следует перейти в алгоритмах от типа real к типу double (или Extended) или полностью перевести все арифметические действия на длинную математику (погрешность 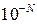 ).
).
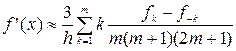 ,
, 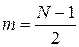 ,
,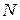 – количество ближайших точек;
– количество ближайших точек;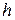 – шаг сетки.
– шаг сетки.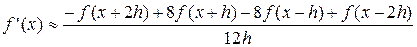 ,
, на отрезке
на отрезке 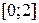 с точностью
с точностью 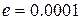 методом касательных.
методом касательных.


