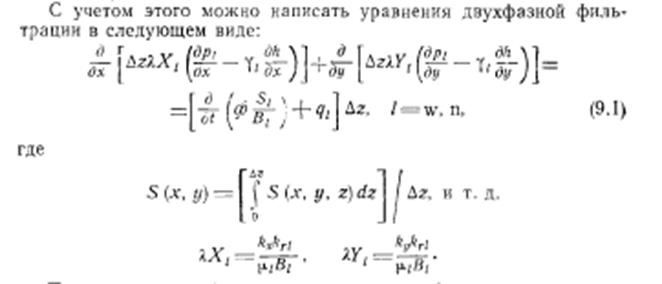Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление дифференциальных уравнений параболического типа в разностной формеСодержание книги
Поиск на нашем сайте Представление дифференциальных уравнений параболического типа в разностной форме Известно, что любую функцию
Отсюда видно, что по известным значениям функции и её производных можно определять значения функции в близлежайшей точке. Пусть на оси OX имеется отрезок MN, разбитый на n равных частей. Тогда расстояние (шаг) между соседними точками 0 1 i-1ii+1 ….. n-1n
O M N Х Выберем произвольные точки на линии MN:(i - 1), i, (i + 1 ) и при помощи (1.1.1) запишем значения функции в точках (i - 1) и (i + 1) через значения функции и её производных в точке i. Для точки (i-1): (x-a) = - h, а для точки (i+1): (x-a) = h.
Здесь Первая производная из уравнений (1.1.2) и (1.1.3) будет выражаться так:
Можно получить более точное выражение для первой производной по x в точке i, если вычесть (1.1.3) из (1.1.2)
Где j – соответствует временному слою Можно получить боле точное выражение первой производной Запишем значение функции
Т.е. с точностью до Рассмотрим представление в конечно – разностной форме одномерного дифференциального уравнения параболического типа
которое описывает фильтрацию сжимаемой жидкости (аналогично уравнению теплопроводности) Используя уравнения (1.1.5) и (1.1.7) предыдущего раздела имеем выражение
Здесь В уравнении (1.2.2) левую часть можно рассматривать на различных временных уровнях: либо на слое j Dt и тогда имеем уравнение
либо на временном слое (j+1) Dt и тогда уравнение (1.2.2) имеет вид
При записи этих уравнений пренебрегается величиной В уравнении (1.2.3) имеется лишь одна неизвестная величина Уравнение (1.2.4), где имеются три неизвестные величины Применяя последовательно уравнение (1.2.3) к каждой точке i сеточной области (с учетом граничных условий), можно получить искомое решение на временном слое Записывая неявное уравнение (1.2.4) для точек Таким образом, использование численных методов сводит интегрирование дифференциального уравнения в частных производных (1.2.1) и соответствующих краевых условий к чисто алгебраической задаче.
Примеры решения площадных и профильных задач двухфазной фильтрации.
Задание начальных и граничных условий в двумерном случае.
Получение замыкающих соотношений для решения трехфазных задач. Таблица 1 Модельные исследования. Применение программ моделирования для составления проекта разработки газонефтяного месторождения и составляет процесс модельного исследования. Он имеет различные стадии. Многие вопросы, которые решаются в процессе проектирования, сходны с вопросами, возникающими при разработке программы, однако здесь они рассматриваются с несколько иной точки зрения. Следует отметить, что данные стадии не являются всеобъемлющими. В некоторых случаях могут быть и другие этапы. Итак, для типичного исследования характерны следующие этапы. 1. Опр-ие и обоснование задач разработки с установлением технических и экономических целей. 2. Сбор имеющихся геолого-промысловых и других данных и принятие решения о получении в случае необходимости дополнительной информации. 3. Интерпретация геолого-промысловой информации о свойствах горных пород. 4. Анализ свойств насыщающих пласты флюидов. 5. Выбор типа математической и разностной модели и ее разработка. 6. Корректировка параметров модели с использованием данных об истории разработки пласта, запасов флюидов и т.п. 7. Прогнозирование поведения пласта при различных технологических воздейств- 8. Технико-экономический анализ результатов расчетов, выдача рекомендаций и технологических решений по разработке залежи. Эти этапы, вообще говоря, достаточно типичны, но для различных задач могут значительно отличаться. На первом этапе важно четко поставить вопросы, на которые необходимо ответить при моделировании. Подход к исследованию зависит от конечной цели. Важны вопросы экономики. Какая система разработки пласта наилучшая? Каковы оптимальные дебиты скважин? Как расположить скважины? На эти и другие вопросы удается ответить в результате технико-экономических расчетов. В других ситуациях необходимо найти, например, решение проблемы увеличения нефтеотдачи нефтяной оторочки. В этом случае возникает задача активного воздействия на разработку, перераспределения отбора флюидов из пласта и т.п. Сбор достоверных данных по всей залежи всегда затруднителен. Особенно это касается больших по размерам пластов. При этом необходимо обращать особое внимание на полноту и надежность данных. На третьем этапе по имеющимся геолого-промысловым данным и физическим свойствам горных пород строится "геологическая модель" пласта. Здесь определяется конфигурация модели, толщины пластов, коэффициенты пористости, проницаемости, флюидонасыщенности и т.п. Анализ данных о свойствах флюидов (данные PVT- исследований) служит для того, чтобы показать, нужно ли учитывать при прогнозных расчетах компонентный состав пластовых флюидов или можно свести сложную углеводородную смесь к упрощенной модельной смеси с ограниченным числом псевдокомпонентов. Все данные о свойствах пласта и флюидов должны быть проверены и аппроксимированы по возможности простыми зависимостями. Разработка численной модели пласта один из самых сложных и ответственных этапов, когда сливаются воедино наука и искусство моделирования. Без сомнения, самая простая модель пласта, отражающая наиболее важные аспекты интересующего нас физического процесса, является наилучшей. Поэтому сначала всегда надо стремится определить, нельзя ли получить ответ с помощью простейшей математической модели. Такой подход обычно приводит к лучшему пониманию поставленной задачи. При выборе модели необходимо учитывать: вид ответов, которые мы хотим получить; их точность; неопределенность знания о границах пласта и имеющихся промысловых данных; неопределенность свойств породы и флюидов; физику реальных процессов и степень их схематизации в модели; погрешности, возникающие из-за допущений, принятых при разработке численной модели; погрешности аппроксимации. Очень важным фактором при разработке численной модели является вопрос о ее размерности, поскольку время расчетов и объем необходимой памяти существенно увеличивается с ростом числа измерений. Следует помнить, что число верных знаков в решении задачи зависит от числа верных знаков исходных данных. Одномерные модели часто используются для оценки упрощенных ситуаций, при наличии ограниченной информации о пласте, моделировании лабораторных экспериментов, для качественной оценки влияния отдельных переменных на результаты. Двумерные модели хорошо описывают реальные пласты с хорошей вертикальной сообщаемостью. Поведение отдельных скважин в большинстве случаев может хорошо описываться при помощи двумерных радиальных моделей. Трехмерные модели надо использовать, когда существует необходимость изучения поведения флюидов в пласте, как по площади, так и по разрезу. Особенно это важно при разработке месторождений со слоистой и зональной неоднородностью, а также для многофазных систем. Иногда при модельном исследовании можно применять последовательно несколько моделей. Например, применение радиальной модели для получения данных о распределении флюидов около скважины и использование этих данных в пространственной (трехмерной) модели месторождения. Размер и ориентация разностной сетки также являются важными факторами, от которых зависит точность решения. Здесь следует помнить следующие простые правила. - Ориентация сетки должна быть согласована с направлением главных осей тензора проницаемости, а в профильных и трехмерных моделях слои модели должны соответствовать геологическим слоям. -Там, где ожидаются наибольшие изменения результатов решения, следует измельчать шаг сетки. -Для получения более точных результатов шаг сетки надо брать мельче в местах неоднородных включений и в районе близко расположенных скважин. -Резкие и большие изменения шагов сетки могут приводить к большим погрешностям аппроксимации. -Там, где это возможно, шаг сетки следует выбирать на основе исследования ее влияния на результаты решения. Если возможен выбор метода решения задачи, то следует выбирать наиболее дешевый и простой, однако при этом необходимо помнить, что самый дешевый метод, как правило, и самый грубый. Способ решения системы алгебраических уравнений также весьма существенен. Для задач малой размерности предпочтительны прямые методы (например, прогонка), для задач большой размерности - итерационные. В случае нелинейных уравнений, когда необходимо на каждом временном слое уточнять коэффициенты, итерационные методы предпочтительнее. Временные шаги выбираются из соображений обеспечения устойчивости и точности решения. При этом максимальный шаг по времени для явных разностных схем непосредственно связан с пространственными шагами сетки. Для неявных разностных схем прямой зависимости шага по времени от шагов по пространству нет. Однако и в этом случае существует ограничение на шаг по времени, связанное с погрешностями аппроксимации дифференциальных уравнений конечно-разностными. Точность решения, как отмечалось, может оцениваться по материальному балансу добываемых из пласта флюидов. Корректировка модели по истории разработки месторождения - важная часть любого исследования. Здесь необходимо сначала так подобрать параметры модели, чтобы результаты расчетов соответствовали истории разработки, а затем можно прогнозировать дальнейшее поведение залежи. В последнее время для определения параметров модели все большее применение находят методы целенаправленного подбора параметров, основанные на теории сопряженных функций и методах возмущений. После того как модель скорректирована и удовлетворительно воспроизводит показатели истории разработки, проводятся расчеты вариантов, прогнозирующих поведение пласта при различных технологических воздействиях. На заключительной стадии модельных исследований проводится анализ полученных результатов. Определяется, достаточна ли полученная информация или требуются дополнительные расчеты. Выдаются рекомендации и решения. (1) 30. Понятие о моделировании. Разработка месторождений углеводородов представляет собой комплексную проблему, для успешного решения которой требуется привлечение знаний и опыта, накопленных в различных областях науки и инженерной практики. Одним из основных инструментов для обоснованного принятия стратегических и тактических решений при разработке месторождений углеводородов является моделирование процессов извлечения нефти и газа. Каждое месторождение уникально, неправильное применение тех или иных методов воздействия на пласт может привести к непоправимым последствиям для разработки, поэтому оценку эффективности различных технологий е учетом особенностей конкретного объекта и прогнозирование поведения этого объекта нецелесообразно осуществлять с помощью предварительного моделирования. Процесс моделирования представляет собой воспроизведение поведения объекта е помощью модели. Важно отметить, что моделирование не заменяет непосредственного изучения объекта, которое и является основным источником информации об объекте, используемой при моделировании. Модели, как правило, бывают двух видов: физические и математические. В большинстве случаев физические модели имеют ту же физическую природу, что и изучаемый объект. Эксперименты на физических моделях проводят для исследования закономерностей изучаемого явления. Масштабные модели строятся с соблюдением принципов подобия. Необходимыми условиями такого моделирования являются геометрическое и физическое подобие модели и натуры. Значения переменных величин, характеризующих явление для модели и для натуры в сходственные моменты времени в сходственных точках пространства, должны быть пропорциональны. Результаты эксперимента поставленных на масштабной модели, могут быть перенесены на изучаемый объект путем пересчета, т.е. умножения каждой из определяемых величин на постоянный для всех величии данной размерности множитель - коэффициент подобия. Однако изготовить полностью подобные модели пластов не представляется возможным, поэтому этот метод моделирования получил широкого распространения при прогнозировании месторождений углеводородов. Элементарные модели обычно используют для проведения лабораторных экспериментов по изучению свойств пород и насыщающих их флюидов. В этих экспериментах как правило, используют реальные или смоделированные пластовые породы и жидкости. Результаты лабораторных исследований являются важным источником информации о пласте. Среди физических моделей отдельную группу составляют аналоговые модели, которые воспроизводят процесс физически подобный оригиналу, но подчиняющийся другой группе физических законов. Например, аналогия между характеристиками и электротехнических процессов использовалась в сетках - электроинтеграторах применяемых для создания электрических моделей нефтяных пластов. В таких моделях перепад давления моделировался электрическим напряжением, дебит жидкости - силой тока, проводимость - электрической проводимостью объем флюидов – электрической емкостью и т.д. Аналоговые модели обычно были очень громоздкими. Перестройка модели была сопряжена со значительными сложностями. Поэтому с появлением компьютеров и развитием вычислительной техники аналоговые модели были практически полностью вытеснены компьютерными математическими моделями. Математическая модель представляет собой приближенное описание поведения изучаемого объекта с помощью математических символов. Процесс математического моделирования - изучения объекта с помощью математической модели - можно условно подразделить на четыре взаимосвязанных этапа: 1. формулирование в математических терминах законов, описывающих поведение объекта; 2. решение прямой задачи, т.е. получение путем исследования модели выходных данных для дальнейшего сопоставления с результатами наблюдений за объектом моделирования; З. адаптация модели по результатам наблюдения, решение обратных задач, т.е. определение характеристик модели, которые оставались неопределенными; 4. анализ модели, ее модернизация по мере накопления новой информации об изучаемом объекте, постепенный переход к новой более совершенной модели. (4) 32. Разномасштабные модели фильтрации.
Процесс моделирования представляет собой воспроизведение поведения объекта с помощью модели. Важно отметить, что моделирование ни в коей мере не заменяет непосредственного изучения объекта, которое и является основным источником информации об объекте, используемой при моделировании. Модели, как правило, бывают двух видов: физические и математические. В большинстве случаев физические модели имеют ту же физическую природу, что и изучаемый объект. Эксперименты на физических моделях проводят для исследования закономерностей изучаемого явления. Масштабные модели строятся с соблюдением принципов подобия [25]. Необходимыми условиями такого моделирования являются геометрическое и физическое подобие модели и натуры: значения переменных величин, характеризующих явление для модели и для натуры в сходственные моменты времени в сходственных точках пространства, должны быть пропорциональны. Результаты экспериментов, поставленных на масштабной модели, могут быть перенесены на изучаемый объект путем пересчета, т.е. умножения каждой из определяемых величин на постоянный для всех величин данной размерности множитель — коэффициент подобия. Однако изготовить полностью подобные модели пластов не представляется возможным, поэтому этот метод моделирования не получил широкого распространения при прогнозировании месторождений углеводородов. Элементарные модели обычно используют для проведения лабораторных экспериментов по изучению свойств пород и насыщающих их флюидов. В этих экспериментах, как правило, используют реальные или смоделированные пластовые породы и жидкости. Результаты лабораторных исследований являются важным источником информации о пласте. Среди физических моделей отдельную группу составляют аналоговые модели, которые воспроизводят процесс физически подобный оригиналу, но подчиняющийся другой группе физических законов. Например, аналогия между характеристиками гидродинамических и электротехнических процессов использовалась в резистивно-емкостных сетках - электроинтеграторах, применяемых для создания электрических моделей нефтяных пластов. В таких моделях перепад давления моделировался электрическим напряжением, дебит жидкости — силой тока, проводимость — электрической проводимостью, объем флюидов - электрической емкостью и т.д. Аналогия между фильтрацией флюидов в пористой среде и потоком ионов в электрическом потенциальном поле использовалась в электролитических моделях пластов. Аналоговые модели обычно были очень громоздкими. Перестройка модели была сопряжена со значительными сложностями. Поэтому с появлением компьютеров и развитием вычислительной техники аналоговые модели были практически полностью вытеснены компьютерными математическими моделями [1,9,15,19,32,50,51]. Математическая модель представляет собой приближенное описание поведения изучаемого объекта с помощью математических символов. Процесс математического моделирования - изучения объекта с помощью математической модели — можно условно подразделить на четыре взаимосвязанных этапа: 1. формулирование в математических терминах законов, 2. решение прямой задачи, т.е. получение путем исследования 3. адаптация модели по результатам наблюдения, решение 4. анализ модели, ее модернизация по мере накопления новой информации об изучаемом объекте, постепенный переход к новой более совершенной модели. (3) 33. Геологические и гидродинамические модели Геологическая модель - Размеры (мощность) - Контур - Насыщенность - Пористость - Стратиграфическая и прочностная структура пласта
Гидродинамические модели • модели двух- и трехфазной фильтрации несмешивающихся жидкостей (модель нелетучей нефти), • модель многокомпонентной фильтрации (композиционная модель), • модель неизотермической фильтрации, • модели физико-химических методов воздействия на пласт (полимерного заводнения, закачки поверхностно-активных веществ, углекислого газа и т. п.), • модели фильтрации в среде с двойной пористостью и с двойной проницаемостью для моделирования процессов в трещиновато-поровых коллекторах.
(5) 34. Существующие лицензированные программные пакеты. Понятие программного продукта.
ECLIPSE (США, Англия) VIP (Европа) Атос (ROXAR) MORE CMG (Азис. X.)
Понятие программного продукта - Одна или пакет программ направленных на решение фильтрационных и вспомогательных задач, таких как представление визуализация исходных данных и результатов и т.д.
(6) 35. Структура типового программного пакета для реализации задач моделирования нефтегазовых месторождений. Основными элементами пакета программ для моделирования пласта являются предпроцессор, постпроцессор и собственно модели фильтрации. На стадии предпроцессора осуществляется ввод данных о строении и свойствах пласта и пластовых жидкостей, в том числе построение и оцифровка разностной сетки, задание скважин, обработка баз данных с информацией о работе скважин, соединение и согласование информации из различных источников, выбор модели фильтрации, характеристик разностной сетки, методов решения системы уравнений. Постпроцессор осуществляет визуализацию результатов расчетов: построение различных карт, графиков, таблиц, анимацию результатов моделирования фильтрационных процессов в пласте. Развитый пакет программ включает в себя несколько моделей фильтрации, которые можно использовать по выбору в зависимости от моделируемого объекта и процесса: 1. модели двух- и трехфазной фильтрации несмешивающихся жидкостей (модель нелетучей нефти), 2. модель многокомпонентной фильтрации (композиционная модель), 3. модель неизотермической фильтрации, 4. модели физико-химических методов воздействия на пласт(полимерного заводнения, закачки ПАВ, углекислого газа и т. п.), 5. модели фильтрации в среде с двойной пористостью и с двойной проницаемостью для моделирования процессов в трещиновато-поровых коллекторах. На разных стадиях моделирования пласта используются специальные опции, такие как масштабирование сеток при переходе от геологической модели к гидродинамической (осреднения данных геологической модели при построении и оцифровке более грубой сетки для моделирования фильтрации), построение сеток различных типов (блочно-центрированной, с распределенными узлами, с геометрией угловой точки, прямоугольной, цилиндрической, криволинейной, полигонов Вороного, гибкой, с локальным измельчением), выбор методов аппроксимации и решения уравнений (явный или неявный, прямой или итерационный,упорядочение и решение систем линейных уравнений,контроль за сходимостью), инициализация (моделирование начального равновесного распределения флюидов в пласте), Представление дифференциальных уравнений параболического типа в разностной форме Известно, что любую функцию
Отсюда видно, что по известным значениям функции и её производных можно определять значения функции в близлежайшей точке. Пусть на оси OX имеется отрезок MN, разбитый на n равных частей. Тогда расстояние (шаг) между соседними точками 0 1 i-1ii+1 ….. n-1n
O M N Х Выберем произвольные точки на линии MN:(i - 1), i, (i + 1 ) и при помощи (1.1.1) запишем значения функции в точках (i - 1) и (i + 1) через значения функции и её производных в точке i. Для точки (i-1): (x-a) = - h, а для точки (i+1): (x-a) = h.
Здесь Первая производная из уравнений (1.1.2) и (1.1.3) будет выражаться так:
Можно получить более точное выражение для первой производной по x в точке i, если вычесть (1.1.3) из (1.1.2)
Где j – соответствует временному слою Можно получить боле точное выражение первой производной Запишем значение функции
Т.е. с точностью до
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.237 (0.012 с.) |

 , непрерывную и имеющую все необходимые производные при x=a, можно представить в виде ряда Тейлора:
, непрерывную и имеющую все необходимые производные при x=a, можно представить в виде ряда Тейлора:



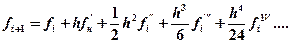

 - значение производных в точке i.
- значение производных в точке i.

 – сумма соответствующих остаточных членов ряда (1.1.2) или (1.1.3), поделённых на h.
– сумма соответствующих остаточных членов ряда (1.1.2) или (1.1.3), поделённых на h.
 .
. 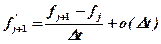
 , а j+1 временному слою (j+1)Δt
, а j+1 временному слою (j+1)Δt по времени через конечные разности.
по времени через конечные разности. и
и  через её значения в точке j+1 с использованием (1.1.1).
через её значения в точке j+1 с использованием (1.1.1).




 , если отбросим остаточные члены о (
, если отбросим остаточные члены о (
 ;
;  ,
,


 - погрешность аппроксимации исходного дифференциального уравнения (1.2.1) конечно – разностным уравнением. Принимается, что
- погрешность аппроксимации исходного дифференциального уравнения (1.2.1) конечно – разностным уравнением. Принимается, что 

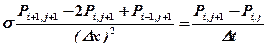

 (Считается, что все величины на временном слое
(Считается, что все величины на временном слое  известны). Такое уравнение называется явным сеточным уравнением.
известны). Такое уравнение называется явным сеточным уравнением. ,
,  называется неявным.
называется неявным. и т.д. Таким образом, оно позволяет явным образом находить решение задачи в каждый момент времени
и т.д. Таким образом, оно позволяет явным образом находить решение задачи в каждый момент времени 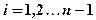 , получаем систему из (n-1) уравнения с (n+1) неизвестным. Граничные условия в точках i=0 и i=n дают еще два условия. Следовательно, чтобы решить задачу на временном слое
, получаем систему из (n-1) уравнения с (n+1) неизвестным. Граничные условия в точках i=0 и i=n дают еще два условия. Следовательно, чтобы решить задачу на временном слое