
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Локально-одномерная схема Самарского А.А.Содержание книги
Поиск на нашем сайте
Рассмотрим следующее дифференциальное уравнение параболического типа
Сейчас, мы рассмотрим разностную схему, которую Самарский А.А. называет локально-одномерной схемой (ЛОС) [26]. Эта схема легко обобщается на случай переменных и разрывных коэффициентов и для произвольной области, а также на многомерный случай. Для этой схемы разностные уравнения для дифференциального уравнения (1.5.1) принимают вид:
Каждая из систем (1.5.9а) и (1.5.9б), вместе с граничными условиями содержит в общем случае (M+1)(N+1) алгебраических уравнений с (М+1)(N+1) неизвестных. Системы имеют трех диагональную матрицу и решаются методом прогонки. Порядок решения системы аналогичен порядку решения системы(1.5.8):.
т.е. сумма значений мощности источника на n+1/2 и n+1 временных слоях равна искомому значению мощности источника. Необходимо отметить, что при использовании ЛОС имеет значение процесс организации прогонки и момент вывода результатов на печать. Решение систем разностных уравнений начинается одной серией прогонок, на пример по оси X. За тем выполняются дважды прогонки по оси Y, дважды по оси X и т. д. Перед выводом на печать результата производится лишь одна серия прогонок по оси X. При выполнении этого правила расчет дает правильные не только количественные, но и качественные результаты. Если это правило не выполняется, то при верных, например, забойных давлениях получаются некачественные карты изобар, построенные по совокупности всех узловых точек области интегрирования.
11.Схематизация залежи в случае однофазной фильтрации. Способ задания реальных скважин на модели. Для задания граничных условий применяются следующие правила: 1.Внешний контур проводится между соседними узлами сетки. 2. Дебиты скважин задаются в виде источников, а сами скважины считаются, расположенными в узлах сетки.
Т.е. На скважинах задаются условия, что мощность источников (
Т.к. мощность источника, это дебит, приходящийся на объем элемента пласта с размерами Действительно, пусть U ij = Где
12.Постановка задачи и основные уравнения при фильтрации многокомпонентных многофазных смесей.(+14) В случае неизотермической фильтрации система (2.1.3) (2.1.4) дополняется уравнением сохранения полной энергии [32,33], которое может быть записано в следующем виде [24]:
где Учитывая,что
или
Уравнение неразрывности для "
где Из (2.1.9) с учетом (2.1.10) имеем:
и
где Так как
имеем окончательно:
Здесь Выражения для Так как пористая среда неподвижна, то В (2.1.16) учитывается, что нефть и вода взаимонерастворимы и тогда
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 840; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.19.29 (0.009 с.) |


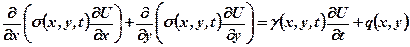

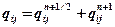
 При такой аппроксимации граничные условия на внешней границе имеют вид (условия непроницаемости контура,
При такой аппроксимации граничные условия на внешней границе имеют вид (условия непроницаемости контура, 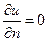 ).
). ;
; 
 ;
; 
 (
( ) и
) и  (
( ) в уравнении (1.5.2)
) в уравнении (1.5.2) )- функция времени, т.е.
)- функция времени, т.е. (1.5.11б)
(1.5.11б) , то, заменяя объем ячейки равновеликим кругом и считая, что в этой области справедлив нелинейный закон фильтрации, например, для идеального газа, можно получить выражения для давления в реальной скважине.
, то, заменяя объем ячейки равновеликим кругом и считая, что в этой области справедлив нелинейный закон фильтрации, например, для идеального газа, можно получить выражения для давления в реальной скважине. , тогда
, тогда  (1.5.12)
(1.5.12)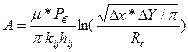 или
или  , при этом
, при этом  ,
,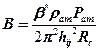
 (2.1.7)
(2.1.7) - пористость в точке пласта, зависящая от давления;
- пористость в точке пласта, зависящая от давления;  - внешнее тепло;
- внешнее тепло;  - внешняя работа на межфазовых поверхностях;
- внешняя работа на межфазовых поверхностях;  - работа сил давления;
- работа сил давления;  - внутренняя энергия фазы;
- внутренняя энергия фазы;  - кинетическая энергия;
- кинетическая энергия;  - потенциальная энергия /остальные обозначения см. выше/.
- потенциальная энергия /остальные обозначения см. выше/.  (2.1.8)
(2.1.8) , где
, где  - удельная парциальная энтальпия,
- удельная парциальная энтальпия,  - удельный парциальный объем,
- удельный парциальный объем,  - удельная парциальная внутренняя энергия, из (2.1.7) имеем
- удельная парциальная внутренняя энергия, из (2.1.7) имеем

 (2.1.9)
(2.1.9) "- го компонента в фазе "
"- го компонента в фазе "  " с учетом фазового перехода можно записать в виде:
" с учетом фазового перехода можно записать в виде: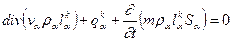 , (2.1.10)
, (2.1.10) - перенос массы компонента "
- перенос массы компонента "  (2.1.11) Примем согласно [126], что
(2.1.11) Примем согласно [126], что (2.1.12)
(2.1.12) - твердая фаза,
- твердая фаза,  - сила межфазового взаимодействия,
- сила межфазового взаимодействия,  - работа на межфазовых поверхностях в единицу времени.
- работа на межфазовых поверхностях в единицу времени.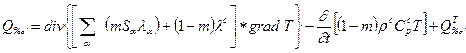 (2.1.13)
(2.1.13) - коэффициент теплопроводности фазы;
- коэффициент теплопроводности фазы;  - коэффициент теплопроводности породы;
- коэффициент теплопроводности породы;  - плотность породы;
- плотность породы;  - теплоемкость породы;
- теплоемкость породы;  - температура;
- температура;  - количество тепла, поступающее через кровлю и подошву пласта.
- количество тепла, поступающее через кровлю и подошву пласта.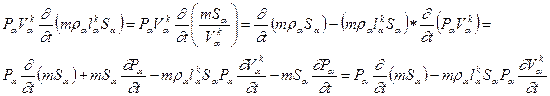 , (2.1.14) то из (2.1.11), пренебрегая
, (2.1.14) то из (2.1.11), пренебрегая  ,
,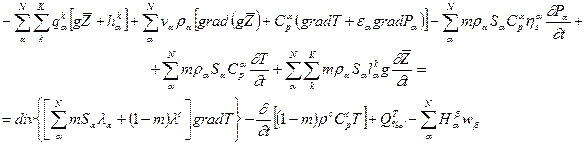 (2.1.15)
(2.1.15) - теплоемкость фазы при постоянном давлении;
- теплоемкость фазы при постоянном давлении;  - коэффициент Джоуля-Томпсона;
- коэффициент Джоуля-Томпсона; 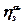 - коэффициент адиабатического расширения фазы /остальные обозначения см. выше/.
- коэффициент адиабатического расширения фазы /остальные обозначения см. выше/. = 0. Далее, пренебрегая величиной
= 0. Далее, пренебрегая величиной 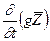 и учитывая, что
и учитывая, что  , имеем из (2.1.15) с использованием (2.1.3) для случая
, имеем из (2.1.15) с использованием (2.1.3) для случая  = 3 и
= 3 и 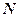 = 3:
= 3:  (2.1.16)
(2.1.16) ,
, , и температуры,
, и температуры, ,
,  - температурный коэффициент расширения,
- температурный коэффициент расширения,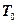 - характерная величина температуры, а замыкающие соотношения:
- характерная величина температуры, а замыкающие соотношения: 



