
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численный метод решения задачи фильтрации многофазной многокомпонентной смеси. Строго неявный метод (SIP).Содержание книги
Поиск на нашем сайте
Система дифференциальных уравнений, описывающую многофазное изотермическое течение многокомпонентной смеси с учетом фазовых переходов компонентов из одной фазы в другую, сжимаемости породы и флюидов и действия гравитационных и капиллярных сил:
здесь
Система (2.1.3) должна быть дополнена следующими замыкающими соотношениями:
В (2.1.4)
Итак, рассматривается течение двухфазной многокомпонентной углеводородной смеси в пласте, которое описывается системой уравнений (2.1.3, 2.1.4). При этом
где
где
При соответствующих граничных условиях решение системы (2.2.2) позволяет получить распределение давления и насыщенности в пласте произвольной формы и толщины с произвольным размещением источников и стоков /скважин/ при учете сжимаемости флюидов и породы, гравитационных и капиллярных сил. Система (2.2.2) в силу ее нелинейности может быть решена только численными методами. В настоящей работе будем применять метод неполной разностной факторизации / SIP- метод/ [14, 29, 42]. Разностные уравнения, аппроксимирующие систему (2.2.2) в матричном виде, выразим так:
Пусть далее
(2.2.3а) и где m - номер итерации. Тогда из (2.2.3а) с учетом (2.2.3б) имеем следующее итерационное выражение:
где
Модифицированная матрица
где Тогда из (2.2.3в) и (а) следует
и далее, если то из (б) следует Решение системы (2.2.3в) можно получить теперь следующим образом. Так как
а затем из (в) определяем вектор приращения
Элемент матрицы в (2.2.3в) для некоторой точки (i, j)пространственной решетки имеет вид:
+ В (2.2.4a) две последние строки выражают вспомогательную матрицу
Выражение (2.2.4а) имеет место при решении разностных уравнений с последовательностью изменения индексов в следующем порядке: i=1,2,…M; j=1,2,…N При порядке просчета с изменением индексов i = I,2,..,M; j= N, N-1,… 2,1 вспомогательная матрица в (2.2.4а) должна быть представлена так:
Мнемоническая схема для решения системы /2.2.3в/ при возрастании индексов имеет вид, представленный на рис.2.1 /черные и светлые кружочки/, при изменении индекса j- в обратном порядке /черные кружочки и крестики/. Следуя работе [273], имеем при возрастании индексов следующие рекуррентные выражения для коэффициентов прогонки:
Вектор
(i=1,2,..., М; j= 1,2, …, N) Значения
При расчете с изменением индексов следующим образом: i = I,2...M; j= N, N-1,...2,1 выражения для коэффициентов имеют вид:
Вектор
(I =1,2, М; j= N, N-1, 2,1) Значения
Пусть далее выражение в квадратных скобках при вычислении в (2.2.5) и (2.2.7) имеет вид
тогда Отсюда следует, что элементы матриц являются строго нижней и верхней треугольными матрицами, равны
и Для улучшения сходимости итерационного процесса при решении разностных уравнений рекомендуется менять порядок расчета от итерации к итерации, а именно, нечетная итерация имеет порядок просчета с изменением индексов i= 1,2,... М; j= 1,2,... N, четная итерация- i=1,2,... М; j = N, N-1,...2, 1 [45]. Затем порядок просчета, повторяется. Элементы матриц
Правая часть уравнения (2.2.3) для некоторой точки (i, j) разностной сетки - вектор вида
и далее,
(k=1, 2) Выражение
В (2.2.11), (2.2.12), (2.2.13) Для улучшения сходимости итерационного процесса применяется матрица итерационных параметров
При этом величины
где
Далее принимаем, что итерационный параметр для лучшей сходимости итерационного процесса изменяется от итерации к итерации [42, 45]
Затем цикл изменения Для улучшения сходимости итерационного процесса можно применить еще и итерационный параметр
/При этом в первом приближении можно брать значения
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.007 с.) |

 (2.1.3)
(2.1.3)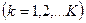
 - пористость в точке пласта,
- пористость в точке пласта,  ,
, - коэффициент, учитывающий упругоёмкость пласта,
- коэффициент, учитывающий упругоёмкость пласта, - коэффициент пористости при атмосферном давлении
- коэффициент пористости при атмосферном давлении  .
. (2.1.4)
(2.1.4)
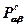 - капиллярное давление между фазами ²
- капиллярное давление между фазами ²  ² и ²
² и ²  ². При этом
². При этом  , где
, где  - безразмерная функция Леверетта,
- безразмерная функция Леверетта,  - контактный угол смачивания [92, 230]. Переменность компонентного состава фаз при фазовых переходах приводит к изменению межфазового натяжения
- контактный угол смачивания [92, 230]. Переменность компонентного состава фаз при фазовых переходах приводит к изменению межфазового натяжения 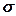 . Последнее выражение (2.1.4), вообще говоря, соответствует условиям статического равновесия при насыщении порового пространства. Однако будем считать, что межфазовый обмен компонентов происходит при относительном движении фаз так же, как и в случае их покоя.
. Последнее выражение (2.1.4), вообще говоря, соответствует условиям статического равновесия при насыщении порового пространства. Однако будем считать, что межфазовый обмен компонентов происходит при относительном движении фаз так же, как и в случае их покоя. = 2 и индекс "1" относится к газу, а индекс "2" к жидкости. С учетом безразмерных соотношений:
= 2 и индекс "1" относится к газу, а индекс "2" к жидкости. С учетом безразмерных соотношений:
 (2.2.1)
(2.2.1)

 характерные значения давления, проницаемости, плотности, вязкости, линейного размера, толщины и глубины залегания пласта, соответственно, индекс " р " - означает размерную величину /остальные обозначения см. выше/. В двумерном случае из (2.1.3) с учетом переменной толщины пласта имеем:
характерные значения давления, проницаемости, плотности, вязкости, линейного размера, толщины и глубины залегания пласта, соответственно, индекс " р " - означает размерную величину /остальные обозначения см. выше/. В двумерном случае из (2.1.3) с учетом переменной толщины пласта имеем: (2.2.2)
(2.2.2)
 - давление в газовой фазе;
- давление в газовой фазе;  - капиллярное давление;
- капиллярное давление; 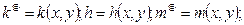
 - зависимость пористости от давления в области, занятой газом;
- зависимость пористости от давления в области, занятой газом;  зависимость пористости от давления в области, занятой жидкостью;
зависимость пористости от давления в области, занятой жидкостью; 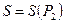 - насыщенность жидкостью порового пространства;
- насыщенность жидкостью порового пространства; ;
;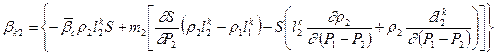 .
.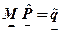 (2.2.3)
(2.2.3)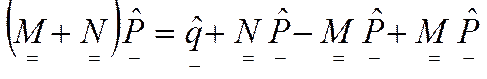
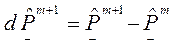 (2.2.3б)
(2.2.3б) (2.2.3в)
(2.2.3в)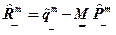 (2.2.3г)
(2.2.3г) - матрица коэффициентов разностных уравнений;
- матрица коэффициентов разностных уравнений; - вспомогательная матрица, определяемая в [42] и позволяющая легко факторизовать систему (2.2.3в);
- вспомогательная матрица, определяемая в [42] и позволяющая легко факторизовать систему (2.2.3в);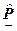 - искомая функция /вектор/;
- искомая функция /вектор/; - вектор, подобный вектору
- вектор, подобный вектору  должна по условию удовлетворять следующему соотношению
должна по условию удовлетворять следующему соотношению (а)
(а) и
и  нижняя и верхняя треугольные матрицы, соответственно.
нижняя и верхняя треугольные матрицы, соответственно. (б)
(б)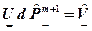 , (в)
, (в)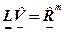 (г)
(г)
 , (д)
, (д) искомых давлений на (m+1) итерации
искомых давлений на (m+1) итерации (е)
(е)
 (2.2.4а)
(2.2.4а)
 ,
, и т.д. матрицы 2-го порядка,
и т.д. матрицы 2-го порядка, ,
,  - диагональная матрица итерационных параметров,
- диагональная матрица итерационных параметров,  - матрицы 2-го порядка, определяемые ниже.
- матрицы 2-го порядка, определяемые ниже.
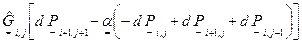 (2.2.4б)
(2.2.4б) (2.2.5)
(2.2.5) при этом определяется /прямая прогонка/ по формуле/2.2.6а/
при этом определяется /прямая прогонка/ по формуле/2.2.6а/ (2.2.6а)
(2.2.6а)
 получаются /обратная прогонка/ по рекуррентной формуле
получаются /обратная прогонка/ по рекуррентной формуле (2.2.6б)
(2.2.6б) (2.2.7)
(2.2.7) (2.2.8а)
(2.2.8а) (2.2.8б)
(2.2.8б) ,
, (2.2.9)
(2.2.9)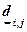 и
и  , которые
, которые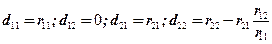 (2.2.10а)
(2.2.10а)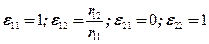 (2.2.10б)
(2.2.10б)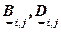 и т.д. в /2.2.4а/ имеют вид:
и т.д. в /2.2.4а/ имеют вид: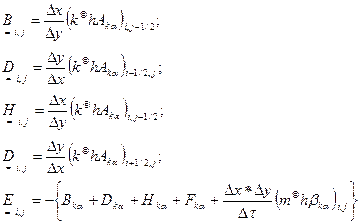 (2.2.11)
(2.2.11)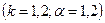

 (2.2.12)
(2.2.12)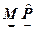 для некоторой точки (i, j)вектор вида
для некоторой точки (i, j)вектор вида (2.2.13)
(2.2.13) - давление на предыдущем временном слое,
- давление на предыдущем временном слое,  - шаги по пространственной и временной разностным сеткам.
- шаги по пространственной и временной разностным сеткам.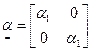
 могут быть получены следующим образом [42]. Из анализа устойчивости разностных уравнений, полученных при рассмотрении линеаризованных дифференциальных уравнений, следует
могут быть получены следующим образом [42]. Из анализа устойчивости разностных уравнений, полученных при рассмотрении линеаризованных дифференциальных уравнений, следует
 - число точек по оси X,
- число точек по оси X, 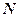 - число точек по оси Y,
- число точек по оси Y,
 (2.2.14)
(2.2.14) до 0 согласно (2.2.14). Следует отметить, что последовательность итерационных параметров может быть как убывающей, так и возрастающей.
до 0 согласно (2.2.14). Следует отметить, что последовательность итерационных параметров может быть как убывающей, так и возрастающей. (2.2.3’г)
(2.2.3’г)  /.
/.


