
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности постановки задач двумерной однофазной фильтрации.Содержание книги
Поиск на нашем сайте
В предыдущем разделе мы рассмотрели весьма эффективный метод решения параболических дифференциальных уравнений – метод прогонки, являющийся специальным методом исключения по Гауссу, т.е. прямым методом. Итерации в этом методе были необходимы лишь при решении уравнений с нелинейными коэффициентами. Процессы неустановившейся фильтрации газа или жидкости в пористой среде, описывающиеся дифференциальными уравнениями в частных производных параболического типа, имеют много аналогов в других разделах математической физики: теории теплопроводности, диффузии и др. При этом следует отметить, что в случае одномерных краевых задач для уравнений параболического типа имеется определенное число аналитических решений и, вообще, все эти задачи более или менее изучены. В настоящее время имеется большое число экономичных методов для многомерных уравнений в частных производных абсолютно устойчивых и требующих порядка Отметим, что получение разностных уравнений аппроксимирующих дифференциальные уравнения в частных производных в многомерном случае совершенно аналогично одномерному случаю. Разница здесь лишь в том, что разложение в ряд Тейлора применено к эллиптическому оператору. Все, что было сказано об устойчивости и сходимости разностных уравнений в одномерном случае в равной мере относится и к многомерным. Поэтому в дальнейшем будем рассматривать лишь неявные схемы разностных уравнений, которые являются абсолютно устойчивыми, по крайней мере, для линейных уравнений. Заметим, что неявные разностные параболические уравнения для фиксированного момента времени являются эллиптическими разностными (сеточными) уравнениями. Поэтому методы решения эллиптических разностных уравнений применимы к уравнениям параболического типа. Рассмотрим следующее дифференциальное уравнение параболического типа
Здесь под x, y- подразумеваются пространственные координаты, t-время, U -искомая функция (P или P 2 в случае газа); s, g -коэффициенты уравнения, зависящие от координат x, y времени t и самой функции U (в линейном случае постоянные), q-мощность источника (стока), приходящейся на объем ячейки. Применяя обычную неявную разностную аппроксимацию к (1.5.1), получим следующую систему разностных уравнений
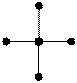
(i, j=1,2…M, N) где Отметим, что рассматривается пока прямоугольная сеточная область. Легко видеть, что система (1.5.2) образует пяти-диагональную матрицу.
Рис.1.2 Обычные прямые методы решения общих систем алгебраических линейных уравнений (метод Гаусса, Жордана, Холецкого и пр.) для системы (1.5.2) непригодны, поскольку требуют порядка 0 Значительно более простыми в отношении программирования являются итерационные методы. и, несмотря на то, что они не приводят за конечное число шагов к точному решению, являются наиболее предпочтительными. Однако простейшие итерационные методы (Гаусса-Зейделя, Якоби) сходятся сравнительно медленно (~ В 1950 Франкел и Янг (независимо) предложили специальный итерационный метод – “экстраполяции Либмана” или “метод последовательной верхней релаксации” (Янг), которые требовали ~ 0( Все эти итерационные методы являются линейными методами в том смысле, что очередное приближение является линейной функцией предыдущего приближения. Есть еще одна группа итерационных методов – вариационные методы: метод наискорейшего спуска, метод сопряженных градиентов. Эти методы построены на принципе минимизации соответствующей квадратичной формы. Мы не будем рассматривать все эти итерационные методы, а остановимся более подробно на методе переменных направлений и на его дальнейшей модификации - суммарной аппроксимации (ЛОС) Самарского А.А.
8.Методы решения двумерных задач фильтрации.(+7) Прежде чем перейти к методу переменных направлений рассмотрим метод матричной прогонки [14, 25].
Тогда в матричной форме можно записать(1.5.2) так,
Пусть решение ищется в виде:
По аналогии с обычной прогонкой имеем:
(i= M-1, …, 1) Метод матричной прогонки по сравнению с обычным методом прогонки относительно громоздок, т.к. требует обращения вспомогательных матриц. Он, вообще говоря, применим лишь для вытянутых прямоугольных областей с малым числом узлов по одной оси. Метод переменных направлений (9вопрос).
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.61.127 (0.01 с.) |

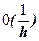 итераций (h - шаг сетки ).
итераций (h - шаг сетки ).
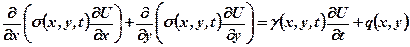
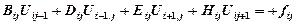
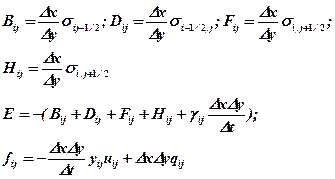




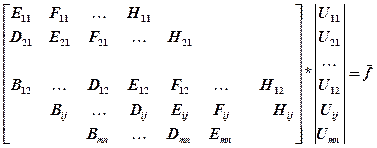
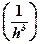 операций (h -шаг сетки). Использование формул Крамера также исключается, т.к. для вычисления определителя N -го порядка требуется ~ N! умножений.
операций (h -шаг сетки). Использование формул Крамера также исключается, т.к. для вычисления определителя N -го порядка требуется ~ N! умножений.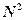 операций или 0(
операций или 0(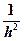 ))
))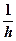 ) итераций. Затем появилось много работ по итерационным методам решения специальных линейных уравнений типа (1.5.2) с применением полиномов Чебышева, которые требуют также ~ 0(
) итераций. Затем появилось много работ по итерационным методам решения специальных линейных уравнений типа (1.5.2) с применением полиномов Чебышева, которые требуют также ~ 0(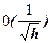 итераций. В том же 1955г. появился метод переменных направлений (Дуглас и Писмен и Речфорд), требующий
итераций. В том же 1955г. появился метод переменных направлений (Дуглас и Писмен и Речфорд), требующий 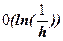 итераций.
итераций.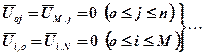
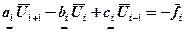 (1.5.4), где
(1.5.4), где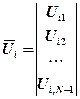 ;
; 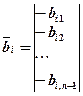 ;
; 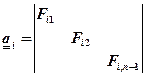
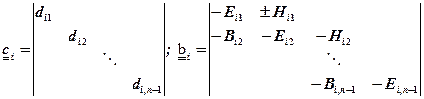
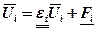 (1.5.5)
(1.5.5) ,
, 
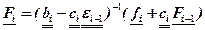 ,
,  (1.5.7)
(1.5.7)


