
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи о притоке реального газа в круговом пласте к скважине. Уравнение, граничные и начальные условия.Содержание книги
Поиск на нашем сайте
Начальные и граничные условия: t = 0 P= Pk = const (1.3.2)
r= R k Далее пусть уравнение состояния для газа имеет вид:
Если газ идеальный, то имеем если газ реальный, то имеем для упругого пласта имеем Для получения универсального решения справедливого для любых рассматриваемых параметров представим дифференциальное уравнение и граничные условия в безразмерном виде, для чего введем безразмерные параметры и переменные:
С учетом (1.3.5) уравнение (1.3.1) и граничные условия (1.3.2) и (1.3.3) имеют вид (для простоты в дальнейшем звездочки будем опускать.)
Уравнение (1.3.1) является общим нелинейным параболическим дифференциальным уравнением. Из него легко получить, например, дифференциальные уравнения для течения идеального газа. Для этого надо положить
Представим теперь задачу (1.3.1’)-(1.3.3’б) в конечно-разностной форме. При этом рассмотрим пространственно-временную непрерывную область в виде сеточной области.
лучшую аппроксимацию, порядка
Для записи разностной схемы уравнения (1.3.1’) поступим следующим образом. Обозначим Правую часть (1.3.1’) представим согласно мнемонической схемы на рис.1.1 и, учитывая, что пространственные разности берутся на верхнем временном слое, имеем после некоторых преобразований
5.Метод прогонки применительно к фильтрации реального газа в круговом пласте.(+4)
Перепишем в общем случае задачу (1.3.8), (1.3.6), (1.3.7) так
Пусть имеет место рекуррентное соотношение:
Подставим в (1.3.9) выражение
Если коэффициенты в точке Затем, зная значения Для определения начальных значений коэффициентов
В нашем конкретном случае имеем (см.1.3.6.)
Итак, для функций Ei и F i имеем формулы прямой прогонки (1.3.13), (1.3.14) Если E n-1 и F n-1 известны, то из граничного условия P n = и P n- 1 = En-1 P n-1+ F n-1 можно получить значение Pn на границе. Т.е.
В нашем случае с учётом (1.3.7) имеем Итак, формулы (1.3.11) и (1.3.15) позволяют определить значения P i для всех значений i = n, n-1…0. (Это формулы обратной прогонки.) 6.Метод прогонки. Основные формулы. Доказательство устойчивости метода.(+4,5)
Перепишем в общем случае задачу (1.3.8), (1.3.6), (1.3.7) так
Пусть имеет место рекуррентное соотношение:
Подставим в (1.3.9) выражение
Если коэффициенты в точке Затем, зная значения Для определения начальных значений коэффициентов
В нашем конкретном случае имеем (см.1.3.6.)
Итак, для функций Ei и F i имеем формулы прямой прогонки (1.3.13), (1.3.14) Если E n-1 и F n-1 известны, то из граничного условия P n = и P n- 1 = En-1 P n-1+ F n-1 можно получить значение Pn на границе. Т.е.
В нашем случае с учётом (1.3.7) имеем Итак, формулы (1.3.11) и (1.3.15) позволяют определить значения P i для всех значений i = n, n-1…0. (Это формулы обратной прогонки.) Формулы прогонки (1.3.13), (1.3.14) и (1.3.15), (1.3.11) были нами получены формально. Мы делили на выражения (b i- c i Ei- 1) и (1-
Для устойчивости метода прогонки достаточно иметь Это действительно так. Рассмотрим разность
Поскольку Отсюда, видно, что Рассмотрим теперь неравенство
т.е. Таким образом, при выполнении условий (1.3.16) разностная задача, решаемая методом прогонки, имеет единственное решение. 1.3.4. В силу того, что решение ведется на ЭВМ приближенно, с конечным числом значащих цифр, возникают ошибки округления. Из-за них фактически находится не функция . Если учесть, что в ходе вычислений возмущающимися являются и коэффициенты
где Первым приближением служат нелинейные коэффициенты, вычисленные по данным решения на j -ом временном слое. Затем определяется приближенное решение на (j +1)-ом временном слое. Во втором приближении для вычисления нелинейных членов используется решение на (j+1)-ом слое. Вновь определяется решение на (j +1)-ом временном слое и т. д., до тех пор, пока не будет выполнено неравенство
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.243 (0.008 с.) |

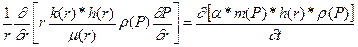 (1.3.1)
(1.3.1)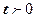 r= R0
r= R0 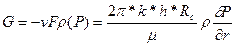 (1.3.3a)
(1.3.3a) (1.3.3б)
(1.3.3б) , (1.3.4a)
, (1.3.4a)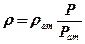 ,
,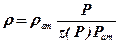 ,
,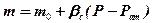 (1.3.4б)
(1.3.4б)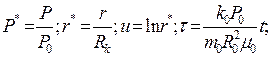
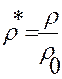 ;
;
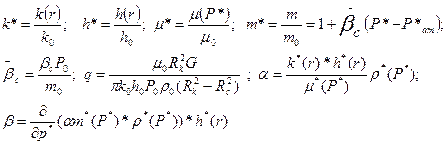
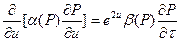
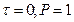
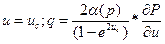
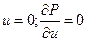
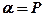 , а
, а 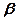 =1.
=1.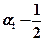 ;
; 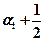
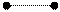
 J+1 J
j-1
J+1 J
j-1
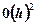
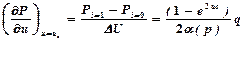
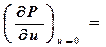

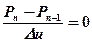
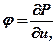 тогда левая часть уравнения (1.3.1’) записывается в виде
тогда левая часть уравнения (1.3.1’) записывается в виде 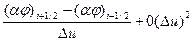 и далее, заменяя
и далее, заменяя 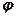 на разности
на разности 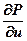 , получим
, получим 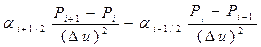
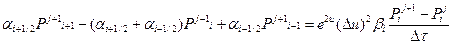
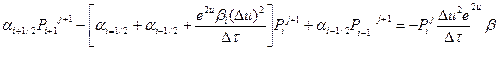
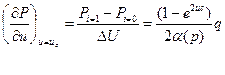 (1.3.6)
(1.3.6) 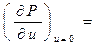
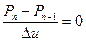 (1.3.7)
(1.3.7)
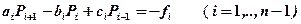
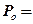
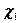
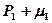 ;
; 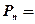
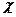
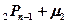 - общий вид граничных условий.
- общий вид граничных условий.
 ,
, 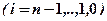
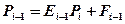 , тогда
, тогда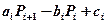
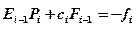
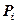 , если:
, если: 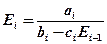 ;
; 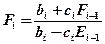
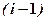 известны, то при помощи формул (1.3.13) можно просчитать коэффициенты
известны, то при помощи формул (1.3.13) можно просчитать коэффициенты 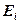 ,
, 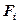 и т. д.
и т. д. по формуле (1.3.11), можно определить значения
по формуле (1.3.11), можно определить значения 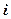 .
.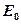 и
и 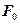 воспользуемся условиями (1.3.10).Тогда будем иметь
воспользуемся условиями (1.3.10).Тогда будем иметь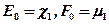
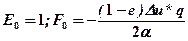
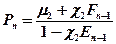
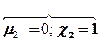
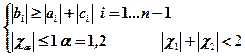
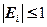 для всех i=1,2,..n-1
для всех i=1,2,..n-1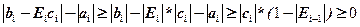 , при
, при 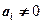 , то
, то 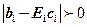 , т.е.
, т.е. 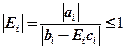 .
.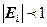 , если
, если 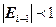 . Тогда все
. Тогда все 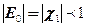 .
.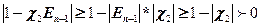 , т.к. или
, т.к. или  , или
, или 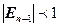 ,
,
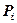 - решение задачи (1.3.9), (1.3.10), а
- решение задачи (1.3.9), (1.3.10), а 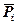 - решение той же задачи с возмущенными коэффициентами
- решение той же задачи с возмущенными коэффициентами 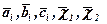 и правыми частями
и правыми частями 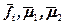 . При этом, если процесс вычислений происходит с возрастанием ошибки округления, то это может привести как к потере точности, так и к невозможности продолжить вычисления из-за роста получаемых величин.
. При этом, если процесс вычислений происходит с возрастанием ошибки округления, то это может привести как к потере точности, так и к невозможности продолжить вычисления из-за роста получаемых величин.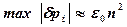 ,
,
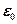 - ошибка округления.
- ошибка округления.



