Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Об активном воздействии на водонапорный режим при разработке газовых месторожденийСодержание книги
Поиск на нашем сайте
Идеология активного воздействия на водонапорный режим подразумевает эксплуатацию обводняющихся и /или/ обводненных скважин с целью отбора пластовой воды и защемленного газа из обводненной зоны пласта [10]. За счет этого создаются условия для: -остановки или замедления движения языков контурной воды вблизи этих скважин; -расширения пузырьков защемленного газа вследствие снижения давления в пласте и создания в обводненной области залежи зон с повышенными фильтрационными сопротивлениями для воды; -добычи защемленного газа при эксплуатации обводняющихся и /или/ обводненных скважин; -увеличения газо- и конденсатоотдачи пластов. Увеличение коэффициентов газо- и конденсатотдачи является конечной целью активного регулирования разработки газовой залежи при водонапорном режиме. Эффективность активного воздействия на водонапорный режим в период прогрессирующего обводнения залежи и в период ее доразработки удается исследовать при применении двухфазной двумерной математической модели, описанной в разделе 2.2.1. Различные случаи применения этой математической модели описаны в работах [10, 7, 6]. При этом рассматривались как плоские двумерные модели, так и профильная модель [10], которая может быть рассмотрена как фрагмент слоистого пласта /типа Оренбургского газоконденсатного месторождения/, у которого имеется хорошо проницаемый пропласток с малыми запасами газа и плохо проницаемые пропластки с большими запасами газа. Отношение проницаемостей составляло 1000:1, а запасов 1:61,5, соответственно. Расчеты, проведенные на этой модели Гордоном В.Я. [10], показали возможности увеличения газоотдачи при активном воздействии на водонапорный режим. Активное воздействие заключалось в отборе части поступающей в вертикальный пласт воды из разгрузочной галереи, расположенной на половине расстояния от контура питания до эксплуатационной галереи /варианты II, Ш, 1У, У/ и при размещении ее на расстоянии X = 0,13 от контура питания /варианты У1, У11/. Первый вариант представлял собой традиционную разработку фрагмента в условиях водонапорного режима, У111 вариант - разработку фрагмента в условиях газового режима. Некоторые результаты расчетов приводятся в таблице 2.1.
Во всех вариантах окончание разработки пласта определялось по достижении на эксплуатационной галереи величины давления, равной 0,01 /безразмерное значение/. Как видно из рассмотрения таблицы 2.1, газоотдача увеличивается с увеличением отбора воды из разгрузочной галереи и приближением ее месторасположения к контуру пласта. При этом в УП варианте конечный коэффициент газоотдачи равен 0,792. За весь период разработки фрагмента пласта в этом варианте отбирается 63%воды, поступающей в пласт. Ценой этого удается довести коэффициент газоотдачи до 0,792, что на 0,296 больше коэффициента газоотдачи, полученного в I варианте. Период разработки пласта в УП варианте меньше, чем в I и 1У вариантах. В УП варианте из эксплуатационной галереи отбирается 43,5% от запасов газа, а из разгрузочной галереи - 35,7%, т.е. с увеличением темпа отбора воды из разгрузочной галереи возрастает и доля газа, добываемого вместе с водой. Уменьшение добычи из эксплуатационной галереи по сравнению с вариантом I объясняется более коротким сроком разработки фрагмента. Коэффициент газоотдачи в варианте УП практически совпадает с коэффициентом газоотдачи в случаегазового режима /вариант У111/. Двумерная двухфазная модель была использована для прогнозирования показателей доразработки обводненных пластов Битковского месторождения при совместном отборе из скважин газа и воды [89]. Проведенные расчеты показали, что доразработка обводненных пластов с отбором газа с водой из обводненных скважин является эффективной и экономически выгодной, способствует регулированию продвижения пластовых вод. В результате уменьшаются размеры обводненной зоны пласта, и возрастает фонд необводненных скважин. Анализ результатов расчетов различных вариантов разработки позволил установить оптимальные дебиты воды из обводненных скважин. Дополнительный коэффициент газоотдачи в оптимальном варианте составил примерно 7%от начальных запасов газа. Показатели разработки слоистого пласта при различных темпах отбора воды и различных положениях разгрузочной галереи
18. Методика решения задачи в случае трехмерной, трехфазной фильтрации (SIP-метод)
где
а индекс "1" относится к газовой фазе, индекс "2" - к нефтяной, индекс "3" - к водяной фазе.
Поскольку система (3.1.3) является существенно нелинейной, возможно получение ее решения только на основе численных методов интегрирования дифференциальных уравнений в частных производных. Методы численного решения подобных систем могут быть различными. В настоящей работе используется метод неполной разностной факторизации [14, 29, 42]. Сущность метода заключается в следующем. Семи диагональная матрица системы разностных /алгебраических/ уравнений /рис.3.1а/, к которой сводится дифференциальная задача (3.1.3), при соответствующих условиях, представляется в виде произведения двух матриц - верхней /рис. 3.1в/ и нижней /рис. 3.1б/ треугольных матриц. Обычное разложение /факторизация/ матрицы Однако матрицу Систему разностных уравнений /аппроксимирующую систему дифференциальных уравнений и граничных условий/ можно записать следующим образом:
Согласно идее рассматриваемого метода решения добавим справа и слева в (3.1.4) вспомогательную матрицу. /Следует отметить, что может быть несколько методов для определения матрицы
где матрица ( Система (3.1.4а) решается, если величины в правой части известны. Для этого применим следующую итерационную схему:
Ряд исследователей указывает, что для улучшения сходимости решения удобней решать задачу не относительно итерируемой величины а относительно вектора невязки /приращений/:
Добавим и вычтем из правой части (3.1.4а) величину
Тогда
или окончательно
где
Здесь и далее
Модифицированная матрица / ( где Из (3.1.4в) и (а) следует, что ( Обозначим тогда из (б) следует
Решение системы (3.1.4в) может быть получено следующим образом. Так как
а затем из (в) определяем вектор приращений
Элемент матрицы в уравнении (3.1.4в) для некоторой точки (i,j,k) пространственной сетки имеет вид:
В (3.1.5) последние 6 строк выражают вспомогательную матрицу
и т.д. - матрицы 3-го порядка в случае трехфазной фильтрации. Выражение (3.1.5) имеет место при решении разностных уравнений с возрастанием всех индексов. Вообще говоря, для улучшения сходимости итерационного процесса при решении разностных уравнений в методе неполной разностной факторизации рекомендуется менять порядок изменения индексов от итераций к итерации. Например, можно менять индексы при нечетной итерации так: i= 1,2,...,М; j= 1,2,…N; k=1,2,…Kz; а при четной i=1,2,...М; j= N,N-1,…2,1; k= Kz, Kz-1,…2,1. На рис.3.2представлена мнемоническая схема для решения системы (3.1.4в) при возрастании всех индексов /черные и светлые кружочки/ и при изменении индексов j и kв обратном порядке /черные кружочки и крестики/. Как было показано выше, процесс решения методом неполной разностной факторизации распадается на два этапа. На первом определяются матрица

(i=1,2,…M; j=1,2,…N; k=1,2,…Kz) Вектор
(i=1,2,…M; j=1,2,…N; k=1,2,…Kz) Значения
(i= M,…2,1; j= N,…2,1; k= Kz,…2,1)
При расчетах с изменением индексов: i=1,2,…M; j=N,N-1,…2,1; k=Kz,Kz-1,…2,1 выражения для коэффициентов имеют вид:
(i=1,2,…M; j=N,N-1,…2,1; k=Kz,Kz-1,…2,1) Вектор
(i=1,2,…M; j=N,N-1,…2,1; k=Kz,Kz-1,…2,1) Значения
(i= M,…2,1; j= 1,2,…N; k= 1,2,…Kz)
В выражениях (3.1.6, 3.1.6', 3.1.7, 3.1.7', 3.1.8, 3.1.8')
Элементы матриц
(m =1,2,3; Правая часть уравнения (3.1.4) для точки (i,j,k)разностной сетки - это вектор вида
и далее
Здесь Для выбора величин итерационных параметров в матрице итерационных параметров рекомендуется рядом исследователей /Уайнштейн и др. 1969 [262,272]/ оценить следующую величину:
где M, N, Kz- число узлов по осям X, Y, Z, соответственно;
Лучшая сходимость итерационного процесса достигается при использовании последовательности итерационных параметров в цикле [45]. Для матрицы итерационных параметров
При этом итерационные параметры изменяются от итерации к итерации в геометрической прогрессии. Согласно (3.1.11) 19. Особенности задания начальных и граничных условий в случае пространственных задач фильтрации Если границы пласта непроницаемы, т.е. поток через такую границу равен нулю, то в рассматриваемом случае это означает, что
На скважинах граничные условия можно задавать в виде плотности /интенсивности/ источника или стока, приходящейся на один узел разностной сетки /как это сделано в системе (3.1.3) /. В случае если не все внешние границы пласта непроницаемы, можно задать величину перетока флюида через внешнюю границу пласта при помощи источников, расположенных в граничных узлах пласта. Например, плотность такого источника по воде можно определить по формуле:
где
времени / n+1 /; При задании начальных условий необходимо учитывать, что флюиды в пласте первоначально находятся при капиллярно-гравитационном равновесии. Для его расчета необходимо знать вид капиллярных кривых для пород рассматриваемого месторождения, /Если таких данных нет, то приходится задаваться гипотетическими зависимостями с тем условием, что размеры переходных зон от одного флюида к другому равняются величине, которая определяется из промысловых данных/. Необходимы также данные о величинах остаточной нефтенасыщенности, водонасыщенности и газонасыщенности. На рис.3.3 приведено примерное распределение по толщине пласта флюидов, находящихся в условиях капиллярно-гравитационного равновесия. Как следует из рассмотрения рис.3.3, весь пласт может быть разделен на пять зон: - Зону газовую, где нефть и вода содержатся как остаточные. - Переходную зону между газом и нефтью, где насыщенности газа и нефти подчиняются капиллярно-гравитационному равновесию, а водонасыщенность равна остаточной. - Зону нефтяную, где газ и вода присутствуют как остаточные, а нефтенасыщенность максимальна.
- Переходную зону между нефтью и водой, где насыщенности нефти и воды подчиняются капиллярно-гравитационному равновесию, а газонасыщенность равна остаточной. - И, наконец, пятую зону - водяную, где насыщенность по воде максимальна, а газ и нефть присутствуют как остаточные. С помощью капиллярных кривых для данного месторождения определяются величины капиллярного давления, соответствующие величинам остаточной водонасыщенности и газонасыщенности, а также величинам максимальной насыщенности по газу и по воде. Пусть для определенности Для определения начальных значений давлений и насыщенностей флюидов в пласте поступаем следующим образом. Сначала, определяем границы зон, которые выделяются на рис.3.3. Следует отметить, что задание начальных условий можно производить как снизу вверх, так и сверху вниз согласно рис.3.3. Рассмотрим способ задания начальных условий сверху вниз. Толщина газовой зоны от кровли пласта до начала переходной зоны задается из промысловых данных и тем самым определяется Величина
где Давление в газовой фазе на границе переходной зоны определяется по формуле:
где Давление в нефтяной фазе на границе переходной зоны, т.е. при
где Толщина нефтяной зоны, R 1, задается по промысловые данным и поэтому величина
Значение
Значение давления в нефтяной фазе на границе с нефтяной зоной определяется так:
Значение давления в нефтяной фазе на границе с переходной зоной между нефтью и водой, т.е. при
Давление в этой же точке в водяной фазе определяется следующим образом:
Величина давления в водяной фазе на границе между водяной зоной и переходной определяется так:
После того, как границы зон и давления на них определены, глубины При
Если
В нефтяной зоне,
При
В водяной зоне, следующим образом:
Задание начальных и граничных условий в двумерном случае.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.017 с.) |


 (3.1.3)
(3.1.3)
 на верхнюю
на верхнюю  и нижнюю
и нижнюю  треугольные матрицы приводит к появлению ненулевых членов в области между диагоналями Z и E для нижней матрицы и в области между диагоналями S и E для верхней матрицы. При значительном числе узлов разностной сетки решение такой факторизованной /т.е. разложенной на множители/ системы требует большой памяти для хранения ненулевых членов матриц и значительных затрат машинного времени на решение.
треугольные матрицы приводит к появлению ненулевых членов в области между диагоналями Z и E для нижней матрицы и в области между диагоналями S и E для верхней матрицы. При значительном числе узлов разностной сетки решение такой факторизованной /т.е. разложенной на множители/ системы требует большой памяти для хранения ненулевых членов матриц и значительных затрат машинного времени на решение. таким образом, чтобы ненулевые члены сохранялись только на диагоналях, представленных на рис. 3.1г. Модифицированная матрица (
таким образом, чтобы ненулевые члены сохранялись только на диагоналях, представленных на рис. 3.1г. Модифицированная матрица ( )легко факторизуется /разлагается/ на произведение матриц
)легко факторизуется /разлагается/ на произведение матриц 
 (3.1.4)
(3.1.4)
 (3.1. 4а)
(3.1. 4а) , где m – номер итерации.
, где m – номер итерации.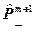
 (3.1.4б)
(3.1.4б)


 , (3.1.4в)
, (3.1.4в) ;
; 
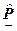 - искомая функция /вектор/;
- искомая функция /вектор/;  - правая часть разностных уравнений /вектор/.
- правая часть разностных уравнений /вектор/.
 ;
; 

 =
=  ;
;  =
= 
 - фазовое давление / давление в фазе/ в точке (i,j,k) разностной сетки;
- фазовое давление / давление в фазе/ в точке (i,j,k) разностной сетки;  - правая часть уравнения (3.1.4) в точке (i,j.k) разностной сетки, соответствующая определенному компоненту смеси / m = 1,2,3/.
- правая часть уравнения (3.1.4) в точке (i,j.k) разностной сетки, соответствующая определенному компоненту смеси / m = 1,2,3/. =
=  (б)
(б) (в)
(в) (г)
(г) (д)
(д) (е)
(е)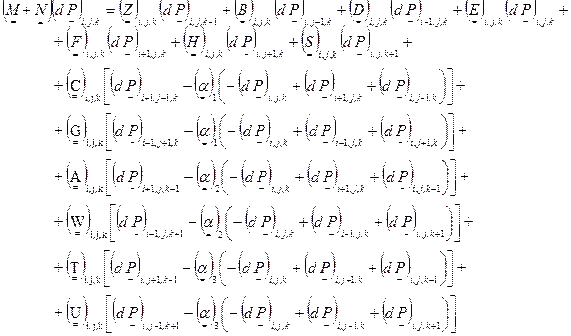 (3.1.5)
(3.1.5) - диагональная матрица итерационных параметров, (p= 1,2,3);
- диагональная матрица итерационных параметров, (p= 1,2,3); - вектор невязки по давлениям в фазах в точке (i,j,k);
- вектор невязки по давлениям в фазах в точке (i,j,k); ;
; 
 , на втором решается система (е), чтобы определить вектор невязки
, на втором решается система (е), чтобы определить вектор невязки  (3.1.6)
(3.1.6)
 (3.1.7)
(3.1.7) (3.1.8)
(3.1.8)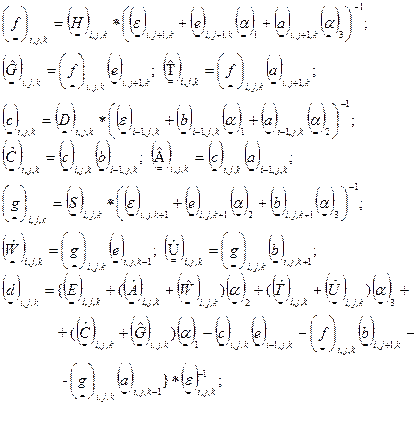 (3.1.6’)
(3.1.6’)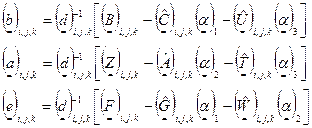
 (3.1.7’)
(3.1.7’) (3.1.8’)
(3.1.8’) - матрица итерационных параметров;
- матрица итерационных параметров;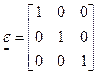 - единичная матрица
- единичная матрица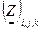 ,
,  и т.д. в /3.1.5/ имеют вид:
и т.д. в /3.1.5/ имеют вид:
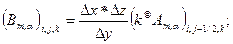




 (3.1.9)
(3.1.9)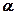 =1,2,3)
=1,2,3)
 (3.1.10)
(3.1.10) ;
;  - фазовое давление (
- фазовое давление ( - размеры шагов пространственной и временной разностной сетки.
- размеры шагов пространственной и временной разностной сетки.
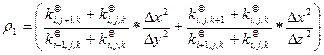 ;
; ;
; .
.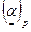 величины
величины  могут быть определены следующим образом:
могут быть определены следующим образом: (3.1.11)
(3.1.11) до 0, затем цикл изменения итерационного параметра повторяется. При оценке
до 0, затем цикл изменения итерационного параметра повторяется. При оценке 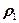 ,
,  ,
,  величины, равные нулю или бесконечности не рассматриваются. В общем случае число параметров в цикле принимается с = 4
величины, равные нулю или бесконечности не рассматриваются. В общем случае число параметров в цикле принимается с = 4  10. Еслипри определенной последовательности решения возникает расходимость результатов, вычисленное значение
10. Еслипри определенной последовательности решения возникает расходимость результатов, вычисленное значение  следует умножить на коэффициент, меняющийся от 2 до 10, если итерации сходятся, но медленно, то это значение нужно разделить на тот же коэффициент.
следует умножить на коэффициент, меняющийся от 2 до 10, если итерации сходятся, но медленно, то это значение нужно разделить на тот же коэффициент. для i=1, 2, … M; j= 1, 2, … N
для i=1, 2, … M; j= 1, 2, … N для i=1, 2, … M; k= 1, 2, … Kz
для i=1, 2, … M; k= 1, 2, … Kz для j=1, 2, … N; k= 1, 2, … Kz
для j=1, 2, … N; k= 1, 2, … Kz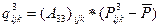 (3.1.13)
(3.1.13) - давление в водяной фазе на границе пласта в момент
- давление в водяной фазе на границе пласта в момент
 - значение давления на момент времени /n + 1 / в водяном пласте, которое можно определить с помощью уравнения материального баланса для водоносного пласта. При этом строение водоносного пласта предполагается известным, а общий приток воды к месторождению определяется как
- значение давления на момент времени /n + 1 / в водяном пласте, которое можно определить с помощью уравнения материального баланса для водоносного пласта. При этом строение водоносного пласта предполагается известным, а общий приток воды к месторождению определяется как 
 - величина капиллярного давления при остаточной газонасыщешюсти;
- величина капиллярного давления при остаточной газонасыщешюсти;  - величина капиллярного давления при максимальной насыщенности по газу;
- величина капиллярного давления при максимальной насыщенности по газу;  - величина капиллярного давления при максимальной водонасыщенности;
- величина капиллярного давления при максимальной водонасыщенности;  . - величина капиллярного давления при остаточной водонасыщенности.
. - величина капиллярного давления при остаточной водонасыщенности. /см. рис.3.3/.
/см. рис.3.3/. определяется из условий капиллярно-гравитационного равновесия по формуле:
определяется из условий капиллярно-гравитационного равновесия по формуле: (3.1.14)
(3.1.14) (3.1.15)
(3.1.15) - давление в газовой фазе на кровле пласта, т.е. при
- давление в газовой фазе на кровле пласта, т.е. при  .
. определяется так:
определяется так: (3.1.16)
(3.1.16) - давление в газовой фазе в точке
- давление в газовой фазе в точке  (3.1.17)
(3.1.17)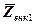 , а, следовательно, и толщины переходной зоны между нефтью и водой при условии капиллярно-гравитационного равновесия определяется по формуле:
, а, следовательно, и толщины переходной зоны между нефтью и водой при условии капиллярно-гравитационного равновесия определяется по формуле: (3.1.18)
(3.1.18) (3.1.19)
(3.1.19) определяется по формуле
определяется по формуле (3.1.20)
(3.1.20) (3.1.21)
(3.1.21) (3.1.22)
(3.1.22) узлов разностной сетки, моделирующей пласт, сравниваются с этими границами и рассчитываются фазовые давления в них.
узлов разностной сетки, моделирующей пласт, сравниваются с этими границами и рассчитываются фазовые давления в них. т.е. в газовой зоне фазовые давления определяются по формулам:
т.е. в газовой зоне фазовые давления определяются по формулам: (3.1.23)
(3.1.23) , то узел находится в переходной зоне между газом и нефтью, и фазовые давления определяются по формулам:
, то узел находится в переходной зоне между газом и нефтью, и фазовые давления определяются по формулам: (3.1.24)
(3.1.24) , фазовые давления определяются следующим образом:
, фазовые давления определяются следующим образом: (3.1.25)
(3.1.25)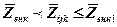 , узел разностной сетки расположен в переходной зоне между нефтью и водой, и фазовые давления определяются так:
, узел разностной сетки расположен в переходной зоне между нефтью и водой, и фазовые давления определяются так: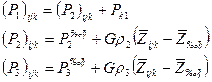 (3.1.251)
(3.1.251) и фазовые давления определяются:
и фазовые давления определяются: