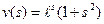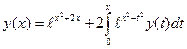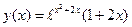Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
интегральных уравнений ВольтерраСодержание книги Поиск на нашем сайте
В полученных выражениях (8.3) коэффициентов ряда Неймана
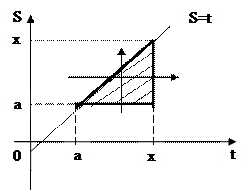
В кратных интегралах изменим порядок интегрирования в соответствии с ниже изображенной областью интегрирования
Как и для интегральных уравнений Фредгольма, приняв за первое итерированное ядро данное ядро, за второе итерированное ядро примем
тогда
Аналогично найдем
где
……………………………………………………………………….. где
……………………………………. Подставим полученные выражения коэффициентов
Выражение в квадратных скобках назовем резольвентой интегрального уравнения Вольтерра второго рода и для нее введем обозначение
Если итерированные ядра найдены, а следовательно и резольвента, то решение интегрального уравнения Вольтерра (8.1) определится по формуле
Аналогично, группируя интегралы попарно в формулах (9.1) для коэффициентов
В формулу резольвенты (9.3) подставив выражения итерированных ядер (9.2)
получим интегральное уравнение резольвенты
Если в формулу резольвенты (9.3) подставить выражения итерированных ядер (9.5), то получим другое интегральное уравнение резольвенты
Пример 10. Построить резольвенту ядра K(x,t) = x – t.
Решение. По формулам (9.2) находим итерированные ядра
и по индукции выписываем
Затем по формуле (9.3) находим резольвенту
Пример 11. Вычислив итерирование ядра и резольвенту, найти решение уравнения
Решение. Положив
Далее по формулам (9.2) найдём
……………………………………………………………………...
По индукции выпишем n-ое итерированное ядро
и по формуле (9.3) найдём резольвенту
Решение интегрального уравнения получим по формуле (9.4)
Ответ: Нетрудно проверить что найденная функция является решением исходного уравнения
!!!§10. Решение уравнений Вольтерра с разностными ядрами с помощью преобразования Лапласа
Преобразование Лапласа для произвольной (комплекснозначной) функции
где Функция Преобразование Лапласа существует для непрерывных и кусочно-непрерывных функций, удовлетворяющих условию Для всякого оригинала f(x) функция Формулу (10.1) кратко будем записывать так:
По известному изображению
где путь интегрирования расположен параллельно мнимой оси комплексной плоскости справа от всех особых точек функции f(p),что соответствует Интеграл в (10.2) понимается в смысле главного значения
Формула (10.2) справедлива для непрерывных функций. В отрицательной области формула (10.2) даёт Если в точке Формулу обращения преобразования Лапласа (10.2) кратко будем записывать так:
Сверткой(по Лапласу) двух функций f(x) и
Справедлива теорема о свертке:
которая часто используется при решении уравнений Вольтерра с разностным ядром [2]. [20], [33]. Уравнения Вольтерра второго рода с ядром, зависящим от разности аргументов, имеют вид
Применяя преобразование Лапласа £ к уравнению (10.3) и учитывая, что интеграл с ядром, зависящим от разности аргументов, по теореме о свертке преобразуется в произведение
Решение уравнения (10.4) определяется формулой
которую можно записать в эквивалентном виде
Применяя к (10.6) обратное преобразование Лапласа, получим решение уравнения (10.3) в виде
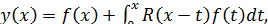 (10.7) (10.7)
где
При использовании формулы (10.7) могут возникнуть технические трудности: 1°. При получении изображения
2°. При нахождении оригинала резольвенты (10.7), изображение которого Для вычисления соответствующих интегралов применяют таблицы прямых и обратных преобразований Лапласа, причем во многих случаях для обратного преобразования используют методы теории функций комплексного переменного, включая теорему о вычетах. Замечание. Если нижний предел в интеграле уравнения Вольтерра с ядром, зависящим от разности аргументов, равен
Схема решения интегральных уравнений Вольтерра второго рода с разностным ядром с помощью интегрального преобразования Лапласа,
Преобразование Лапласа можно применить для решения систем интегральных уравнений Вольтерра вида
Подействуем на систему преобразованием Лапласа. Тогда будем иметь
Решая эту систему линейных алгебраических уравнений, определим
Пример 12. Рассмотрим уравнение
которое является частным случаем уравнения (10.3) Сначала, используя таблицы преобразований Лапласа, получим образ ядра интегрального уравнения в виде
Затем по формуле (10.6) найдем образ резольвенты
Используя далее таблицы обратных преобразований Лапласа, получим оригинал резольвенты
Заметим, что в частном случае при
Пример 13. Решить интегральное уравнение:
Решение. Известно, что
Пусть
Отсюда
или
Следовательно, решение данного интегрального уравнения есть
§11. Задачи для самостоятельного решения 1. Проверить, что заданная функция является решениями следующих интегральных уравнений: 1) Ответ: является решением.
2) Ответ: не является решением. 3) Ответ: является решением. 2. Составить интегральные уравнения, соответствующие следующим начальным задачам: 1) 2) Ответ: 3) Ответ: 4) Ответ: 3. Выписать интегральные уравнения Фредгольма, эквивалентные следующим интегральным уравнениям Вольтерра: 1) 4. Решить интегральные уравнения Вольтерра, применив метод дифференцирования: 1) 2) 3) 4) 5. Найти решение интегральных уравнений Вольтерра, применив степенные ряды: 1) 2) 6. Найти решение интегральных уравнений Вольтерра, применив метод последовательных приближений: 1) 2) 3) 4) 5) В следующих уравнениях найти приближенное решение на отрезке 6) Ответ: 7) Ответ: 8) Ответ: 9) Ответ: 7. Найти решения уравнений Вольтерра, применив ряд по степеням параметра: 1) 2) 8. Найти решение уравнений Вольтерра, вычислив итерированные ядра и резольвенту: 1) Ответ: 2) Ответ: 3) Ответ: 4) Ответ: 5) Ответ:
Литература
1. Васильева А.Б., Медведев Т.Н., Тихонов Н.А., Уразгильдина Т.А. «Дифференциальные и интегральные уравнения. Вариационное исчисление» - М., 2003.
2. Васильева А. Б., Тихонов Н. А. «Интегральные уравнения» - М.: Физматлит, 2002. 3. Виарда Г. Интегральные уравнения, ГТТИ, 1933. 4. Вольтерра В., Теория функционалов, интегральных и интегро-дифференциальных уравнений. – М.: Наука, 1982. 5. Вольтерра В. Математическая теория борьбы за существование. Наука, физматлит. М, 1976. -286с. 6. Трикоми Ф. Интегральные уравнения. ИЛ, 1960. 7. Забрейко П. П., Кошелев А. И. и др. Интегральные уравнения. – М.: Наука, 1968. 8. Канторович Л. В., Крылов В. И. Приближенные методы высшего анализа. – М.: Наука, 1962. 9. Краснов М. Л. Интегральные уравнения. Введение в теорию. – М.: Наука, 1975. 10. Краснов М. Л., Кисилев А. И., Макаренко Г. И. «Интегральные уравнения» - М.: УРСС., 2003. 11. Лизоркин П. И. Курс дифференциальных и интегральных уравнений с дополнительными главами анализа. – М.: Наука, 1965. 12. Ловит У. В. Линейные интегральные уравнения. – М.: Госиздат., 1957. – 266с. 13. Люстерник Л. А., Соболев В. И. Краткий курс функционального анализа. // М.: Высшая школа, 1982. 14. Миргород В.Ф. «Обобщение методов аналитического решения некоторых типов интегральных уравнений Вольтерра второго рода»/ ОАО «Элемент», г. Одесса, Украина 2009. 15. Михлин С. Г. «Интегральные уравнения и их приложения» - М.: ОГИЗ., 1949. 16. Михлин С. Г. Лекции по линейным интегральным уравнениям. Физматгиз, 1959. 17. Михлин С. Г., Смолицкий Х. Л. Приближенные методы решения дифференциальных и интегральных уравнений. – М.: Наука, 1965. 18. Петровский И. Г. «Лекции по теории интегральных уравнений» - М.: УРСС., 2003. 19. Привалов И. И. Интегральные уравнения. ОНТИ, 1937. 20. Полянин А. Д., Манжирова А. В. «Справочник по интегральным уравнениям» - М.: Физматлит, 2003. 21. Тихонов А. Н., Самарский А. А. «Численные методы» 22. Цлаф Л. Я. «Вариационное исчисление и интегральные уравнения» - издательство «Лань», 2005. 23. Volterra V. Lesons sur les equations integrals et les equations integrals et les equations integrodifferentielles. - Paris.1913 24. Volterra V. Varigzioni e fluttuzioni del numero d' indivindin specie animali conviventi // R. Comit Tallas. Jt. Met.31.1927. 25. Volterra V. La teoria deifunzionall appiata aifenomene ereditari // Atti congr.lut. Mat., Bolongna,v.1,1928. 26. Volterra V. Sulla inversion degli integrali definite. Rend. Accad. Lincei, 1896, 5. p. 177-185. 27. Volterra V. Theory of functional and of integral and integro – differenstial equations. - London – Grasqov, 1930. 28. Volterra V. Theory of functional and of integral and integro – differenstial equations.- London 1931. 29. Volterra V. The general equations of biological strife in the case of historical actions // Proc. Edinburgh Math.Soc.6.1939.- C/ 4-10. 30. www.intuit.ru 31. www.wikipedia.ru 32. www.eqworld.ipmnet.ru 33. www.yabotanik.ru
СОДЕРЖАНИЕ Введение…………………………………………………………………. 3 §1. Классификация интегральных уравнений Вольтерра……………...7
§2. Задачи, приводящие к интегральным уравнениям Вольтерра…...11 §3. Интегральные уравнения Вольтерра как частный случай уравнений Фредгольма…………………………………………………19 §4. Решение интегральных уравнений Вольтерра методом дифференцирования…………………………………………………….20 §5. Решение интегральных уравнений Вольтерра с помощью степенных рядов………………………………………………………...22 §6. Решение интегральных уравнений Вольтерра методом последовательных приближений………………………………………25 §7. Уравнения с вырожденными ядрами………………………………32 §8. Решение уравнений Вольтерра с помощью ряда Неймана………37 §9. Итерированные ядра и резольвента интегральных уравнений Вольтерра………………………………………………………………..40 §10.Ррешение уравнений Вольтерра с разностными ядрами с помощью преобразования Лапласа…………………………………….45 §11. Задания для самостоятельного решения…………………………55 Литература………………………………………………………………60
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.61.190 (0.012 с.) |

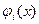 последовательно произведем подстановку
последовательно произведем подстановку 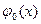 в
в 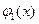 , затем
, затем 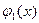 в
в 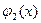 и так далее, сменив обозначения переменных
и так далее, сменив обозначения переменных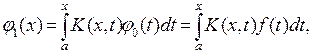 .
.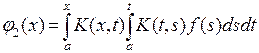 .
.
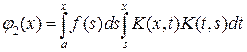 .
.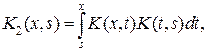
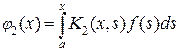 .
.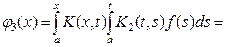
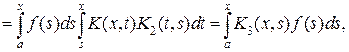
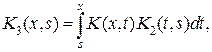
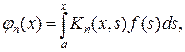 (9.1)
(9.1)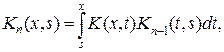 (9.2)
(9.2)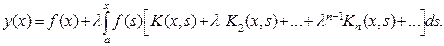
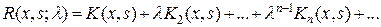 (9.3)
(9.3)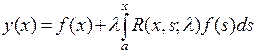 . (9.4)
. (9.4)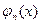 начиная с последней пары, для итерированных ядер получим другую формулу
начиная с последней пары, для итерированных ядер получим другую формулу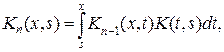 n=2,3,…. (9.5)
n=2,3,…. (9.5)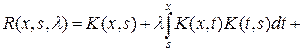
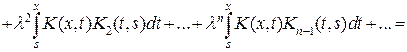
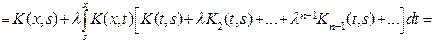
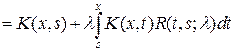
 (9.6)
(9.6)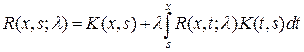 . (9.7)
. (9.7)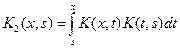
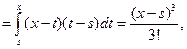
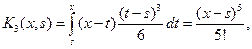 …………..,
…………..,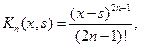 …………..
…………..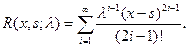
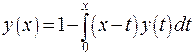 .
.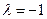 , выпишем ядро
, выпишем ядро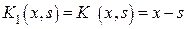 .
.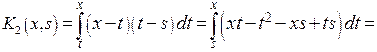
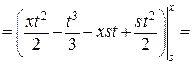
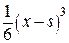 ,
,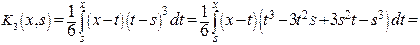

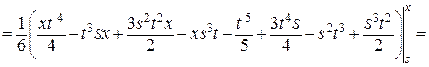
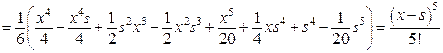 ,
,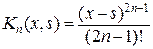
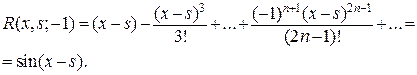 .
.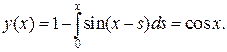
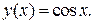
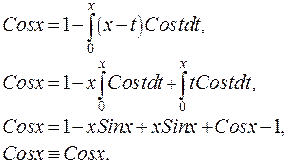
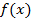 действительного переменного
действительного переменного 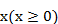 определяется следующим образом:
определяется следующим образом: (10.1)
(10.1)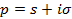 – комплексная переменная.
– комплексная переменная.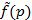 –изображением (образом) функции
–изображением (образом) функции 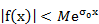 , где
, где 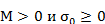 - некоторые числа. Далее считаем, что в указанной оценке взято наименьшее из возможных чисел
- некоторые числа. Далее считаем, что в указанной оценке взято наименьшее из возможных чисел 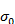 , которое называется показателем ростафункции f(x).
, которое называется показателем ростафункции f(x).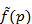 определена в полуплоскости
определена в полуплоскости 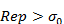 и является в этой полуплоскости аналитической функцией.
и является в этой полуплоскости аналитической функцией.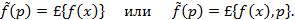
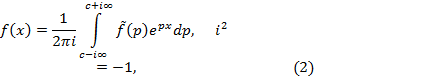 (10.2)
(10.2)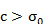 .
.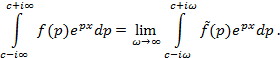
 .
.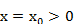 , функция f(x)имеет конечный разрыв первого рода, то правая часть формулы (10.2) в этой точке дает значение
, функция f(x)имеет конечный разрыв первого рода, то правая часть формулы (10.2) в этой точке дает значение 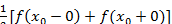 (при
(при 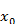 первый член в квадратных скобках должен быть опущен).!!!
первый член в квадратных скобках должен быть опущен).!!!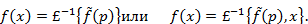
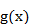 называется выражение
называется выражение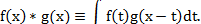 !!!
!!!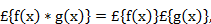
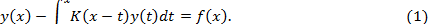 (10.3)
(10.3)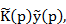 приходим к уравнению для образа искомой величины
приходим к уравнению для образа искомой величины (10.4)
(10.4) (10.5)
(10.5)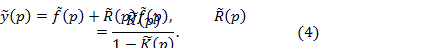 (10.6)
(10.6)
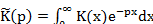 для конкретного ядра
для конкретного ядра 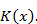
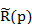 находится по формуле (10.6).
находится по формуле (10.6).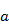 , то его можно свести к уравнению вида (10.3) с помощью замены
, то его можно свести к уравнению вида (10.3) с помощью замены 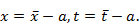
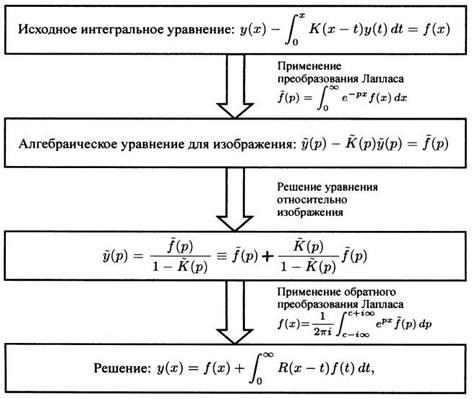 На рисунке приведена принципиальная схема решения интегральных уравнений Вольтерра второго рода с разностным ядром с помощью интегрального преобразования Лапласа.
На рисунке приведена принципиальная схема решения интегральных уравнений Вольтерра второго рода с разностным ядром с помощью интегрального преобразования Лапласа.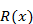 –оригинал функции
–оригинал функции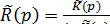 .
.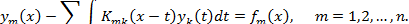
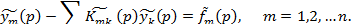
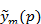 , и решение рассматриваемой системы примет вид [2], [20]
, и решение рассматриваемой системы примет вид [2], [20]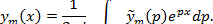
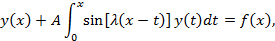
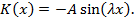
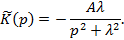
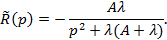
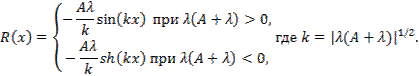
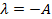 получаем
получаем 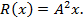 Подставляя эти выражения в формулу (10.7), находим решение интегрального уравнения. В частности, при
Подставляя эти выражения в формулу (10.7), находим решение интегрального уравнения. В частности, при 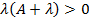 это решение имеет вид [20]
это решение имеет вид [20]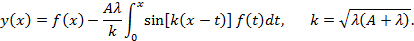
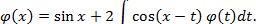

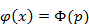 . Применяя преобразование Лапласа к обеим частям уравнения и учитывая при этом теорему умножения (изображения свертки), получим
. Применяя преобразование Лапласа к обеим частям уравнения и учитывая при этом теорему умножения (изображения свертки), получим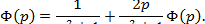
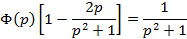
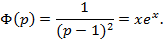
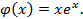
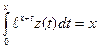 ,
, 
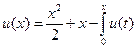 ,
, 
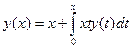 ,
, 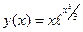
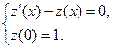 Ответ:
Ответ: 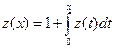 .
.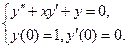
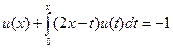 , где
, где 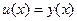 .
.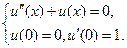
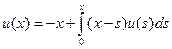 .
.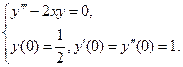
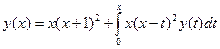 .
.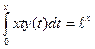 , 2)
, 2) 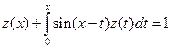 .
.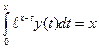 . Ответ:
. Ответ: 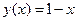 .
.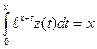 . Ответ:
. Ответ: 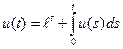 . Ответ:
. Ответ: 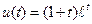 .
.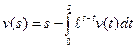 . Ответ:
. Ответ: 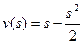 .
.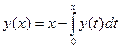 . Ответ:
. Ответ: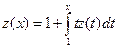 . Ответ:
. Ответ: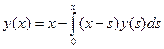 . Ответ:
. Ответ: 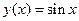 .
.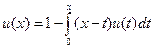 . Ответ:
. Ответ: 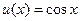 .
.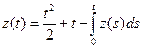 . Ответ:
. Ответ: 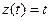 .
.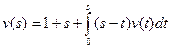 . Ответ:
. Ответ: 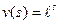 .
.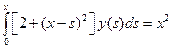 . Ответ:
. Ответ: 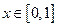 с точностью
с точностью 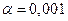 :
: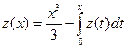 .
.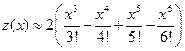 .
.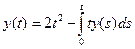 .
.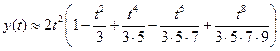 .
.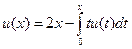 .
.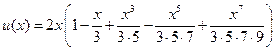 .
.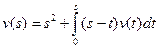 .
.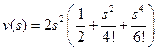 .
.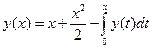 . Ответ:
. Ответ: 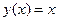 .
.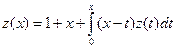 . Ответ:
. Ответ: 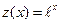 .
.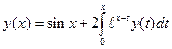 .
.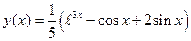 .
.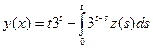
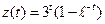 .
.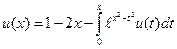 .
.
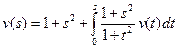 .
.