Опишите основные свойства прямых и итерационных методов решения уравнений.
Опишите основные свойства прямых и итерационных методов решения уравнений.
Методы численного решения системы (1) делятся на две группы: прямые методы («точные») и итерационные методы.
Прямыми методами называются методы, позволяющие получить решение системы (1) за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
Итерационные методы (методы последовательных приближений) состоят в том, что решение системы (1) находится как предел последовательных приближений  при при  , где n номер итерации. При использовании методов итерации обычно задается некоторое малое число e >0 и вычисления проводятся до тех пор, пока не будет выполнена оценка , где n номер итерации. При использовании методов итерации обычно задается некоторое малое число e >0 и вычисления проводятся до тех пор, пока не будет выполнена оценка  . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д. . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д.
Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.
5. Что понимают под сходимостью итерационной процедуры? Ответпоясните примерами.
Итерационный процесс - последовательное приближение и проверка условия достижения искомого результата. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма.
Проверкасходимости итерационного процесса выполняется по относительным приращениям обобщенных деформаций на данной итерации. Большее из двух относительных приращений обобщенных деформаций сравнивается с заданным критерием сходимости. В случае неудовлетворения заданному критерию итерационный цикл повторяется. В противном случае итерационный процесс заканчивается и найденные на последней итерации компоненты напряжений и жесткости сечений являются окончательными расчетными. [ 1 ]
Критериемсходимости итерационного процесса является сравнение двух последующих величин сх и су.
Пример в курсовой – сравнение abs(f)<0.00001
Что такое область сходимости применительно к итерационной процедуре?
Говорят, чтоитерационный процесс сходится, если при выполнении последовательных итераций получаются значения корней, все ближе и ближе приближающиеся к точному значению корня. В противном случае итерационныйпроцесссчитается расходящимся.
Перепишем для удобства уравнение (1) в виде:
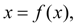 (3) (3)
что можно получить путем замены:  . .
Пусть  – нулевое приближение, т.е. начальное приближенное значение корня уравнения (3). Тогда в качестве следующего, 1-го, приближения примем – нулевое приближение, т.е. начальное приближенное значение корня уравнения (3). Тогда в качестве следующего, 1-го, приближения примем

следующим, 2-м, приближением будет
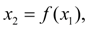
и т.д., в качестве n -го приближения примем
 (4) (4)
Здесь возникает главный вопрос: приближается ли  к истинному решению уравнения (3) при неограниченном возрастании n? Иными словами, сходится ли итерационный процесс (4)? к истинному решению уравнения (3) при неограниченном возрастании n? Иными словами, сходится ли итерационный процесс (4)?
Уловия сходимости метода итераций [2]: если при всех значениях  , вычисляемых в процессе (4) решения задачи: , вычисляемых в процессе (4) решения задачи:
1)  , то итерационный процесс сходится; , то итерационный процесс сходится;
2)  , то итерационный процесс расходится. , то итерационный процесс расходится.
Если производная  в некоторых точках в некоторых точках  по модулю меньше 1, а в других точках по модулю меньше 1, а в других точках  – больше 1, то ничего определенного о сходимости итерационного процесса сказать нельзя. Он может как сходиться, так и расходиться. – больше 1, то ничего определенного о сходимости итерационного процесса сказать нельзя. Он может как сходиться, так и расходиться.
Если итерационный процесс расходится, то причиной этого часто является неудачный выбор нулевого приближения. Так, на рис. 1 показано, что выбор нулевого приближения существенно влияет на сходимость итерационного процесса. Это напрямую связано с тем, находится ли нулевое приближение 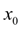 в области, где выполняются условия сходимости итерационного процесса. в области, где выполняются условия сходимости итерационного процесса.

Рис. 1. Зависимость сходимости итерационного процесса от выбора нулевого приближения
Процесс (4) считается завершенным, если 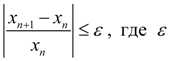 – заданная точность решения. – заданная точность решения.
Поясните, что такое скорость сходимости и как она связана с эффективностью метода.
Почему на практике часто применяют комбинированные алгоритмы, включающие в себя различные методы отыскания корней?
Опишите основные свойства прямых и итерационных методов решения уравнений.
Методы численного решения системы (1) делятся на две группы: прямые методы («точные») и итерационные методы.
Прямыми методами называются методы, позволяющие получить решение системы (1) за конечное число арифметических операций. К этим методам относятся метод Крамера, метод Гаусса, LU-метод и т.д.
Итерационные методы (методы последовательных приближений) состоят в том, что решение системы (1) находится как предел последовательных приближений  при при  , где n номер итерации. При использовании методов итерации обычно задается некоторое малое число e >0 и вычисления проводятся до тех пор, пока не будет выполнена оценка , где n номер итерации. При использовании методов итерации обычно задается некоторое малое число e >0 и вычисления проводятся до тех пор, пока не будет выполнена оценка  . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д. . К этим методам относятся метод Зейделя, Якоби, метод верхних релаксаций и т.д.
Следует заметить, что реализация прямых методов на компьютере приводит к решению с погрешностью, т.к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.
5. Что понимают под сходимостью итерационной процедуры? Ответпоясните примерами.
Итерационный процесс - последовательное приближение и проверка условия достижения искомого результата. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма.
Проверкасходимости итерационного процесса выполняется по относительным приращениям обобщенных деформаций на данной итерации. Большее из двух относительных приращений обобщенных деформаций сравнивается с заданным критерием сходимости. В случае неудовлетворения заданному критерию итерационный цикл повторяется. В противном случае итерационный процесс заканчивается и найденные на последней итерации компоненты напряжений и жесткости сечений являются окончательными расчетными. [ 1 ]
Критериемсходимости итерационного процесса является сравнение двух последующих величин сх и су.
Пример в курсовой – сравнение abs(f)<0.00001
|