
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фрактальные методы анализа случайно-неоднородных средСодержание книги
Поиск на нашем сайте
В настоящее время довольно часто находят применение методы анализа поведения излучения в случайно-неоднородных средах, основанные на фрактальных и мультифрактальных представлениях о структуре сигнала и среды, в которой они распространяются. Необходимость использования понятия фрактала обусловлена тем, что далеко не все задачи, относящиеся к характеристике свойств неупорядоченных сред, могут решаться методами традиционной статистической физики. Полный успех при использовании этих методов достигается только в предположении либо абсолютной хаотичности сред и происходящих в ней процессов, либо в предположении их полной упорядоченности. За пределами возможностей последовательной статистической теории часто оказывается описание неупорядоченных сред и процессов, в которых отсутствуют как полная упорядоченность, так и полный хаос. Примером таких сред может служить атмосфера Земли. Учитывая, что трассы в открытой тропосфере – это трассы, для которых характерно стохастическое поведение, можно утверждать, что поведение сигнала на таких трассах непредсказуемо, и применение детерминистических закономерностей становится невозможным, да и неоправданным. Их изучение требует применения методов статистического анализа. Особенность применения фрактальных методов в том, что они дают как локальные характеристик, так и (в результате усреднения по большим интервалам) глобальные характеристики изучаемого процесса. С математической точки зрения фрактал – это множество с дробной размерностью. Топологическая размерность для точки равна нулю, для линии – единице, для поверхности – двум и так далее. Как представить множество с размерностью 3/2? По-видимому, для этого нужно что-то промежуточное между длиной и площадью. И, если длину представить мерой единица, а площадь – мерой два, то нужна мера 3/2. Такую
Перед тем, как оценивать фрактальные свойства атмосферной турбулентности, с целью лучшего понимания привлекаемых представлений рассмотрим фрактальную структуру вещества. Известно, что конденсированное состояние вещества может существовать не только в форме плотной сплошной среды, но и в виде сильно разрыхленных пористых структур. Такого рода структуры образуются, как правило, в результате конденсации в сложных неравновесных условиях при слипании движущихся по определенному закону твердых частиц. Рассмотрим образование конденсированных сред, первая из которых имеет обычную компактную структуру, а вторая – рыхлую, фрактальную. Если образование является компактным, число структурных элементов (атомов, молекул, частиц) в зародыше новой фазы размера R определяется соотношением:
где d - размерность пространства. Такой же вид функциональной зависимости характерен и для выделенного объема
оказывается величиной, не зависящей от размера. Здесь через В случае некомпактных сред картина совсем другая. Для рыхлого фрактального агрегата размера
где В результате плотность
при
Таким образом, одной из основных характеристик фрактальной системы является фрактальная размерность. И она не совпадает с размерностью того пространства, в котором фрактал образуется. Такой же подход к изучению фрактальной структуры вещества может быть использован для анализа свойств атмосферной турбулентности. Представим область, в которой движется турбулентная воздушная масса, разбитой на ячейки с ребром
Как показали многие авторы, применявшие различные модели, при d =3 Теперь рассмотрим основные соотношения, позволяющие проводить фрактальный анализ флуктуационных характеристик электромагнитных сигналов. Представим некоторый случайный процесс
Пусть это приращение имеет гауссовское распределение с нулевым математическим ожиданием и дисперсией
Отсюда вытекают соответствующие выражения для дисперсии и математического ожидания при любых
Входящий в эти соотношения параметр
для любого Свойство самоподобия определяет масштабную инвариантность фрактала, - так называемый скейлинг. Для реального естественного фрактала существует, очевидно, определенный масштаб скейлинга, характеризующий интервал между некоторыми минимальными и максимальными масштабами длины, вне пределов которого свойство самоподобия пропадает.
Статистическое самоподобие сигнала определяет фрактальную структуру графика
На практике для определения параметра Херста обычно используют соотношение
которое является следствием (202) и свидетельствует, что величина Участки, для которых D >1, характеризуют сигнал, обладающий фрактальными свойствами. Близость значения D к единице на определенном участке прямой говорит об отсутствии фрактальных свойств у сигнала на соответствующем участке (см. рис.). Существует отдельный класс неоднородных фрактальных объектов, для полного описания которых недостаточно введения лишь одной фрактальной размерности D и необходим целый спектр таких размерностей. Такие объекты носят название мультифракталов. Наряду с чисто геометрическими характеристиками, определяемыми параметром D, такие фракталы обладают еще и некоторыми статистическими свойствами. Идея мультифрактального анализа состоит в разложении анализируемого анализируемого множества со сложной статистикой по множествам однородных фракталов с четко выраженной фрактальной размерностью. Для характеристики мультифрактального множества используют понятие функции мультифрактального спектра или спектра сингулярностей мультифракталов. Таким образом, мультифрактал представляется как объединение различных однородных фрактальных подмножеств, каждое из которых имеет собственное значение фрактальной размерности. Понятие о вейвлет-преобразованиях
Важной частью обработки сложных сигналов стало использование вейвлет анализа. Оно позволяет получить дополнительные по сравнению с обычным статистическим анализом характеристики сигналов и расширить подходы к оценке параметров скейлинга. Вейвлеты представляют собой особые функции в виде коротких волн (всплесков) с нулевым интегральным значением и с локализацией по оси независимой переменной (t или x), способных к сдвигу по этой оси и масштабированию (растяжению или сжатию). Любой из наиболее часто используемых типов вейвлетов порождает полную ортогональную систему функций. В случае вейвлет-анализа (декомпозиции) процесса (сигнала) в связи с изменением масштаба вейвлеты способны выявить различие в характеристиках процесса на различных шкалах, а посредством сдвига можно проанализировать свойства процесса в различных точках на всем исследуемом интервале. Именно полнота такой системы позволяет осуществить восстановление (реконструкцию или синтез) процесса посредством обратного вейвлет- преобразования.
Вейвлеты широко применяются для исследования нестационарных сигналов, неоднородных полей и изображений различной природы и временных рядов, для распознавания образов и в решении многих радиотехнических и радиофизических задач, связи, электронике, акустике метеорологии и т.д. Итак, вейвлет-преобразование одномерного сигнала состоит в его разложении по базису, сконструированному из обладающей определенными свойтвами солитоноподобной функции, - вейвлета, - с помощью масштабных перемещений и переносов. Каждая из функций этого базиса характеризует и определенную частоту (пространственную или временную), и ее локализацию в физическом пространстве (времени). Преобразование Фурье К понятиям вейвлет-анализа обычно подходят путем аналогий с преобразованиями Фурье. Пусть существует пространство квадратично интегрируемых функций
Он может быть представлен ортогональной системой функций
Здесь коэффициенты
в котором
Базисная функция
Вейвлет-преобразование одномерного сигнала – это представление его в виде обобщенного ряда или интеграла Фурье по системе базисных функций
сконструированных из материнского (исходного) вейвлета Таким образом, для заданных а и b функция
(а) (b) Рис.2 Вейвлет «Мексиканская шляпа» (а) и модуль его спектральной плотности (b) Малые значения а соответствуют мелкому масштабу Таким образом, в частотной области спектры вейвлетов похожи на всплески (волночки) с пиком на частоте Следовательно, вейвлеты локализованы как во временной, так и частотной областях. Вообще вейвлеты занимают промежуточное положение между синусоидами и дельта-образными импульсными функциями. Следует отметить, что спектральное представление (образ) вейвлетов аналогично заданию окна в оконном преобразовании Фурье. Но отличие состоит в том, что свойства окна (его ширина и перемещение по частоте) присущи самим вейвлетам. Это служит предпосылкой их адаптации к сигналам, представляемым совокупностью вейвлетов. Поэтому нетрудно понять, что с помощью вейвлетов можно осуществить анализ и синтез локальной особенности любого сигнала Отметим главные признаки вейвлета:
1. Ограниченность: квадрат нормы функции должен быть конечным:
2. Локализация: Вейвлет-преобразование, в отличие от преобразования Фурье, использует локализованную исходную функцию и по времени, и по частоте. Отметим, что дельта-функция и гармоническая функция не удовлетворяют необходимому условию одновременной локализации во временной и частотной областях. 3. Нулевое среднее:
Из этого условия становится понятным выбор названия «вейвлет» – маленькая волна. Равенство нулю площади функции 4. Характерным признаком вейвлет-преобразования является его автомодельность или самоподобие. Все вейвлеты конкретного семейства
Существует ряд часто принимаемых вейвлетов. Примером простейшего ортогонального вейвлета служит HAAR-вейвлет:
Недостатком этого вейвлета являются его несимметричность и негладкость. Каждый вейвлет имеет определенные особенности во временном и частотном пространстве. Но, поскольку некоторые важные свойства вейвлет-преобразования не зависят от выбора вейвлета, такой анализ позволяет получить и объективную информацию об анализируемом сигнале. Непрерывное вейвлет-преобразование Как мы говорили, с помощью непрерывных масштабных преобразований и переносов вейвлета
На основе этой системы записываются интегральное (непрерывное) вейвлет-преобразование функции
Здесь
В этих обозначениях выражение в круглых скобках в ( 4 ) означает скалярное произведение соответствующих сомножителей, Вейвлет-спектр Нужно иметь в виду, что коэффициенты На рисунке в качестве примера приведены результаты применения вейвлет-преобразования для анализа зарегистрированных в эксперименте флуктуаций интенсивности лазерного излучения на наклонной трассе длиной 320 м в приземном слое и флуктуаций температуры в точке приема. Ри с.Временные изменения локальной интенсивности лазерного излучения на наклонной трассе (верхняя кривая слева) и временные флуктуации температуры в пункте приема в двух точках, разнесенных на расстояние 1 см (верхняя кривая справа). Внизу – соответствующие картины вейвлет-коэффициентов (a – масштабный коэффициент, b – параметр сдвига)
Применение описанного метода позволяет, в частности, увидеть cкрытую периодичность флуктуаций исследуемого сигнала, которую не представляется возможным проследить с помощью общепринятых методов исследования. Наблюдаемые на рисунке коэффициентов ветвления отдельных участков могут свидетельствовать о фрактальных особенностях в структуре электромагнитного излучения, а, следовательно, и среды распространения сигнала, - канала. А.Н.Яковлев. Введение в вейвлет-преобразования. Изд НГТУ Новосибирск, 2003
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 378; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.187.121 (0.012 с.) |

 -меру определил Хаусдорф для любого
-меру определил Хаусдорф для любого 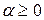 . Каждому множеству в евклидовом пространстве он сопоставил число, которое назвал метрической размерностью. Он же привел первые примеры множеств с дробной размерностью. Выяснилось, что именно она характеризует канторово множество, кривую Коха и другие необычные объекты. Идеи Хаусдорфа были впоследствии развиты Безиковичем. И размерность Хаусдорфа-Безиковича получила широкое применение в ряде разделов математики. Широкому применению этих понятий в других областях (включая гуманитарные проблемы) способствовали работы В. Мандельброта, который и ввел понятие фрактала, - по-латыни это означает «дробный». Ё Он впервые привел примеры некоторых фрактальных явлений в природе. Им же отмечено основное свойство фракталов: если разбить фрактал на сколь угодно малые части, каждая из них оказывается просто уменьшенной копией целого. Это свойство получило название самоподобия. Оно резко отличает фракталы от объектов классической геометрии.
. Каждому множеству в евклидовом пространстве он сопоставил число, которое назвал метрической размерностью. Он же привел первые примеры множеств с дробной размерностью. Выяснилось, что именно она характеризует канторово множество, кривую Коха и другие необычные объекты. Идеи Хаусдорфа были впоследствии развиты Безиковичем. И размерность Хаусдорфа-Безиковича получила широкое применение в ряде разделов математики. Широкому применению этих понятий в других областях (включая гуманитарные проблемы) способствовали работы В. Мандельброта, который и ввел понятие фрактала, - по-латыни это означает «дробный». Ё Он впервые привел примеры некоторых фрактальных явлений в природе. Им же отмечено основное свойство фракталов: если разбить фрактал на сколь угодно малые части, каждая из них оказывается просто уменьшенной копией целого. Это свойство получило название самоподобия. Оно резко отличает фракталы от объектов классической геометрии.
 , (195)
, (195) , где
, где  - геометрический фактор, учитывающий форму выделения. Если выделение имеет равноосную форму, то при размерностях d=1, 2, 3
- геометрический фактор, учитывающий форму выделения. Если выделение имеет равноосную форму, то при размерностях d=1, 2, 3 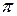 или
или  . Тогда плотность компактного выделения
. Тогда плотность компактного выделения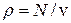 (196)
(196) обозначен объем.
обозначен объем. число частиц определяется как
число частиц определяется как , (197)
, (197) - фрактальная размерность. Она не совпадает с размерностью пространства d для плотного состояния, что и определяет аномальный характер этой зависимости.
- фрактальная размерность. Она не совпадает с размерностью пространства d для плотного состояния, что и определяет аномальный характер этой зависимости. (198)
(198) для рыхлой структуры будет убывающей функцией размера. Это отражает некомпактный характер фрактала, тогда как для компактного образования от размера частиц не зависит (196). Чем больше различие между фрактальной
для рыхлой структуры будет убывающей функцией размера. Это отражает некомпактный характер фрактала, тогда как для компактного образования от размера частиц не зависит (196). Чем больше различие между фрактальной  , соответствующим колмогоровскому масштабу. В фиксированный момент времени движение в одних ячейках будет ламинарным, - безвихревым,- в других – турбулентным. Под действием вязкости вихри такого масштаба быстро затухают. Пусть
, соответствующим колмогоровскому масштабу. В фиксированный момент времени движение в одних ячейках будет ламинарным, - безвихревым,- в других – турбулентным. Под действием вязкости вихри такого масштаба быстро затухают. Пусть  - вероятность, с которой турбулизована данная ячейка. Если
- вероятность, с которой турбулизована данная ячейка. Если  , турбулизованных ячеек нет. При
, турбулизованных ячеек нет. При  турбулизованными оказываются все ячейки. Существует некоторая критическая концентрация при вероятности
турбулизованными оказываются все ячейки. Существует некоторая критическая концентрация при вероятности 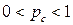 , при которой впервые возникает бесконечный кластер из турбулизованных ячеек. И тогда ситуация резко меняется. До его появления вся вводимая в область движения энергия шла на увеличение числа турбулизованных ячеек и диссипацию. С появлением кластера эта энергия может отводиться по нему из области турбулентного движения. При этом концентрация турбулизованных ячеек при наличии такого кластера может флуктуационно возрастать. Но новые ячейки под действием вязкости будут затухать, поскольку постоянного подвода к ним энергии не будет. В сам о м бесконечном кластере устойчивым будет лишь скелет, состоящий из множества ячеек, принадлежащих бесконечному множеству путей по кластеру. Как уже было сказано, под действием вязкости конечные ветки кластера будут затухать. Образуемые в таких системах критические кластеры представляют собой фрактальные объекты. Можно показать, что универсальный критический параметр
, при которой впервые возникает бесконечный кластер из турбулизованных ячеек. И тогда ситуация резко меняется. До его появления вся вводимая в область движения энергия шла на увеличение числа турбулизованных ячеек и диссипацию. С появлением кластера эта энергия может отводиться по нему из области турбулентного движения. При этом концентрация турбулизованных ячеек при наличии такого кластера может флуктуационно возрастать. Но новые ячейки под действием вязкости будут затухать, поскольку постоянного подвода к ним энергии не будет. В сам о м бесконечном кластере устойчивым будет лишь скелет, состоящий из множества ячеек, принадлежащих бесконечному множеству путей по кластеру. Как уже было сказано, под действием вязкости конечные ветки кластера будут затухать. Образуемые в таких системах критические кластеры представляют собой фрактальные объекты. Можно показать, что универсальный критический параметр  зависит только от топологической размерности пространства, поскольку характеристический размер вихревого кластера вблизи
зависит только от топологической размерности пространства, поскольку характеристический размер вихревого кластера вблизи  определяется соотношением:
определяется соотношением: . (199)
. (199) . Определим его приращение во времени:
. Определим его приращение во времени: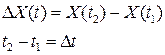 . (200)
. (200) при
при  (
( - положительная константа):
- положительная константа): . (201)
. (201) и
и  :
: . (202)
. (202) носит название параметра Хёрста. Удовлетворяющий этим соотношениям сигнал будет обладать свойством статистического самоподобия, то есть
носит название параметра Хёрста. Удовлетворяющий этим соотношениям сигнал будет обладать свойством статистического самоподобия, то есть (203)
(203) .
.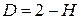 . (204)
. (204) , (205)
, (205) определяется тангенсом угла наклона зависимости
определяется тангенсом угла наклона зависимости  от
от  .
. с конечной энергией:
с конечной энергией: ,
,  .
. , то есть
, то есть (1)
(1) определяются из соотношения
определяются из соотношения ,(2)
,(2)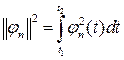 - квадрат нормы или энергия базисной функции
- квадрат нормы или энергия базисной функции  . При этом считается, что никакая из базисных функций не равна тождественно нулю и на интервале ортогональности
. При этом считается, что никакая из базисных функций не равна тождественно нулю и на интервале ортогональности  выполняется условие:
выполняется условие: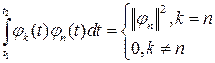 .
.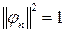 , называется нормированной (или нормальной), а вся система функций
, называется нормированной (или нормальной), а вся система функций  , входящие в (2), представляют собой спектральную составляющую сигнала
, входящие в (2), представляют собой спектральную составляющую сигнала  называется спектром сигнала (рис.) Суть спектрального анализа сигнала
называется спектром сигнала (рис.) Суть спектрального анализа сигнала  ,
, , обладающего определенными свойствами за счет операций сдвига во времени (b) и изменения временного масштаба (a). Множитель
, обладающего определенными свойствами за счет операций сдвига во времени (b) и изменения временного масштаба (a). Множитель  обеспечивает независимость нормы этих функций от масштабирующего числа a.
обеспечивает независимость нормы этих функций от масштабирующего числа a. и есть вейвлет, порождаемый материнским вейвлетом
и есть вейвлет, порождаемый материнским вейвлетом 
 ), большие параметры
), большие параметры  - крупному масштабу
- крупному масштабу  и полосой Δω, т.е. имеют вид полосового фильтра; при этом
и полосой Δω, т.е. имеют вид полосового фильтра; при этом  .
. .
. этой функции равно нулю при ω = 0 и имеет вид полосового фильтра. При различных значениях a это будет набор полосовых фильтров.
этой функции равно нулю при ω = 0 и имеет вид полосового фильтра. При различных значениях a это будет набор полосовых фильтров.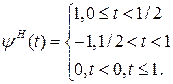
 .(4)
.(4) - нормирующий коэффициент:
- нормирующий коэффициент: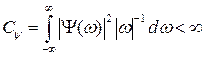
 - фурье-преобразование вейвлета
- фурье-преобразование вейвлета  в отличие от Фурье-спектра является функцией двух аргументов: первый - временной масштаб а - аналогичен периоду осцилляций, то есть обратен частоте, а второй b аналогичен смещению сигнала во времени.
в отличие от Фурье-спектра является функцией двух аргументов: первый - временной масштаб а - аналогичен периоду осцилляций, то есть обратен частоте, а второй b аналогичен смещению сигнала во времени.



