
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная и выборочная совокупности. Распределение случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основным методом испытаний в математической статистике является выборочный метод. В самой общей форме он выглядит следующим образом. Имеется некоторая большая совокупность N объектов, называемая генеральной совокупностью. Генеральная совокупность - это как правило, лишь воображаемое, гипотетическое полное собрание объектов (людей, животных, растений или вещей), являющееся источником данных. Из этой совокупности извлекаются n объектов, которые образуют выборку (выборка – часть генеральной совокупности, взятая для исследования); число n называется объемом выборки. Эти n объектов подвергаются детальному исследованию, по результатам которого требуется описать всю генеральную совокупность или какие-нибудь ее свойства, характеристики. Выборочный метод применяют при исследовании семян на всхожесть, при различных демографических и экономических исследованиях, при контроле за производством и в медицинских исследованиях. На первый взгляд этот метод мало чем отличается от обычного метода малых проб. Например, при анализе вещества все исследования проводят над малыми количествами (пробами) этого вещества. Однако разница тут есть и весьма существенная: при анализе вещества мы заведомо знаем, что интересующий нас признак (количество тех или иных ионов) распределен по всей массе вещества равномерно и, следовательно, любая малая проба является точной копией всей совокупности вещества. При выборочном же методе исследуемый признак распределен по генеральной совокупности неравномерно, причем даже характер этой неравномерности неизвестен. Поэтому далеко не всякая выборка хорошо отражает структуру всей генеральной совокупности. Представьте себе, что вы хотите исследовать средний рост жителей некоторого города, а вам в качестве выборки предлагают сборную баскетбольную команду. Нетрудно понять, насколько будет искажен результат. Не имея никаких сведений о генеральной совокупности, мы, делая выборку, можем полагаться только на случай – все прочие способы отбора будут необъективными, носящими следы влияния посторонних факторов. Все объекты нужно отбирать совершенно случайным образом. Иное дело, если мы заранее знаем, что генеральная совокупность состоит из нескольких классов, различных по своим характеристикам. При этих условиях случайную выборку лучше делать из каждого класса в отдельности. Например, изучая рост жителей, делают отдельную выборку мужчин, отдельную – женщин; иногда при этом учитывают возраст, профессию, место жительства. Выборка, отражающая свойства генеральной совокупности называется представительной или репрезентативной. Из случайного характера выборки вытекает, что любое суждение о генеральной совокупности по выборке само является случайным. Набор допустимых значений хi сам по себе очень слабо характеризует случайную величину. Для того, чтобы полностью охарактеризовать случайную величину, а тем более делать дальнейшие прогнозы, необходимо не только указать, какие значения хi она может принимать, но и как часто она принимает эти значения. Иными словами, нужно задать распределение этой случайной величины. Способы задания случайных величин Описание совокупности значений случайной величины с указанием вероятности каждого значения называется законом распределения этой величины. В более общем случае, чтобы задать закон распределения дискретной случайной величины, нужно просто выписать все ее значения и при каждом из них соответствующую частость Pi (или частоту появления mi). Обычно такую запись оформляют в виде таблицы, где верхняя строка содержит значения случайной величины, а нижняя – вероятности этих значений (или частоту появления mi). Полученная таблица называется законом распределения случайной величины. Этот вид задания распределения случайной величины называется табличным. Рассмотрим примеры таких таблиц. После получения (тем или иным способом) выборочной совокупности все ее объекты обследуются по отношению к определенной случайной величине – т.е. обследуемому признаку объекта. В результате этого получают наблюдаемые данные, которые представляют собой множество расположенных в беспорядке чисел. Такой ряд данных обычно называют статистическим рядом. Анализ таких данных весьма затруднителен, и для изучения закономерностей полученные данные подвергаются определенной обработке. Пример 1 [3]: На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие 60 значений: 3; 1; 3; 1; 4; ï 2; 2; 4; 0; 3; ï 0; 2; 2; 0; 2; ï1; 4; 3; 3; 1; 4; 2; 2; 1; 1; ï 2; 1; 0; 3; 4; ï 1; 3; 2; 7; 2; ï0; 0; 1; 3; 3; 1; 2; 4; 2; 0; ï 2; 3; 1; 2; 5; ï 1; 2; 4; 2; 0; ï 2; 3; 1; 2; 5. Очевидно, что число X является дискретной случайной величиной, а полученные данные есть значения этой случайной величины. Анализ исходных данных в таком виде весьма затруднителен. Простейшей операцией является ранжирование опытных данных, результатом которого являются значения, расположенные в порядке возрастания или убывания. После проведения операции ранжирования опытные данные объединяют так, чтобы в каждой группе значения случайной величины были одинаковы. Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных называется вариантом, а изменение этого значения – варьированием. Варианты будем обозначать строчными буквами с соответствующими порядковому номеру группы индексами Численность отдельной группы сгруппированного ряда данных называется частотой mi, где i – индекс варианта, а отношение частоты данного варианта к общей сумме частот называется частостью (или относительной частотой) и обозначается
Дискретным вариационным рядом называется ранжированная совокупность вариантов xi с соответствующими им частотами mi или частностями В результате проделанных операций были получены семь значений случайной величины (варианты): 0; 1; 2; 3; 4; 5; 7. При этом значение 0 в этой группе встречается 8 раз, значение 1 – 17 раз, значение 2 – 16 раз, значение 3 – 10 раз, значение 4 – 6 раз, значение 5 – 2 раза, значение 7 – 1 раз. Таким образом, получен дискретный ряд, в котором приведены вычисленные значения частот и частостей: Таблица 1.2 Вариационный ряд
В отличие от исходных данных этот ряд позволяет делать некоторые выводы о статистических закономерностях. Если число возможных значений дискретной случайной величины достаточно велико или наблюдаемая случайная величина является непрерывной, то строят интервальный вариационный ряд, под которым понимают упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частностями попаданий в каждый из них значений случайной величины. Как правило, частичные интервалы, на которые разбивается весь интервал варьирования, имеют одинаковую длину и представимы в виде
Длину ∆x следует выбирать так, чтобы построенный ряд не был громоздким, но в то же время позволял выявлять характерные изменения случайной величины. Рекомендуется для ∆x использовать следующую формулу
Число интервалов определяют по формуле Стерджесса: Если окажется, что ∆x – дробное число, то за длину интервала следует принять либо ближайшую простую дробь, либо ближайшую целую величину. При этом необходимо выполнение условий:
После нахождения частных интервалов определяется, сколько значений случайной величины попало в каждый конкретный интервал. При этом в интервал включают значения большие или равные нижней границе и меньшие верхней границы. Пример 2. [3]: При изменении диаметра валика после шлифовки была получена следующая выборка (объемом n=55):
Решение. Так как наибольшая варианта равна 23.8, а наименьшая 10.1, то вся выборка попадает в интервал (10, 24). Мы расширили интервал (10.1, 23.8) для удобства вычислений. По формуле Стерджесса получим семь частичных интервалов. Длина каждого частичного интервала равна В результате весь диапазон данных разделяется на следующие интервалы:
Соответствующий интервальный вариационный ряд называют сгруппированным, он представлен в следующей таблице: Таблица 1.3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 953; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.008 с.) |

 , где n – число групп. При этом имеет место
, где n – число групп. При этом имеет место  .
.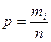 ,
,  , т.е.
, т.е.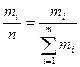 .
. . Статистический ряд, упорядоченный в порядке возрастания или убывания называется вариационным рядом.
. Статистический ряд, упорядоченный в порядке возрастания или убывания называется вариационным рядом.






 , где k - число интервалов.
, где k - число интервалов. , где xmax, xmin – наибольшее и наименьшее значения случайной величины.
, где xmax, xmin – наибольшее и наименьшее значения случайной величины. .
. .
. .
. причем в первый интервал попадает два значения СВ, во второй – четыре и т.д.
причем в первый интервал попадает два значения СВ, во второй – четыре и т.д.


