
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие генеральной совокупности и выборки. Репрезентативность выборкиСодержание книги
Поиск на нашем сайте
2. Какую информацию о групповых свойствах отражает среднее значение. Приведите пример. 3. Какую информацию о групповых свойствах отражает дисперсия, коэффициент вариации, стандартное отклонение. Приведите пример практического использования этих характеристик. 4. Какую информацию о групповых свойствах отражает медиана. Приведите пример. В чем различия между медианой и средним значением, в каких случаях они совпадают и не совпадают. Как определить в каких пределах лежат все значения признака в генеральной совокупности Дайте интерпретацию стандартной ошибки среднего, как ее уменьшить Дайте определение квартилей. Какую информацию о групповых свойствах отражают нижний и верхний квартили.
Задание к теме СРСП 1: Сравните две группы с указанием: a) Величины, вокруг которой группируются значения данногопризнака в каждой группе. Обоснуйте свой ответ. b) Являются ли первая и вторая группа однородными по данному признаку. Обоснуйте свой ответ. c) В какой группе разброс значений больше. Обоснуйте свой ответ. d) Какая величина встречается наиболее часто в каждой из групп E) На что указывает медиана признака в каждой из групп F) На что указывает межквартильный размах в каждой из групп. g) Предположив, что признак имеет нормальное распределение, определите в каких пределах лежат 95,44% всех значений признака в генеральной совокупности H) Представьте результаты вычислений в графическом виде
СРСП 2. Проверка гипотезы о нормальности распределения случайной величины.
Для проверки нормальности распределения случайной величины можно использовать коэффициент ассиметрии и коэффициент эксцесса. Коэффициент ассиметрии As – показатель отклонения кривой распределения от симметричности.
Отрицательный коэффициент ассиметрии означает, что кривая распределения скошена влево от центра, положительный – вправо. При нормальном распределении As близок к нулю. Коэффициент эксцесса Ex характеризует степень заостренности кривой распределения (отрицательный коэффициент свидетельствует о об более острой вершине, положительный – о более пологой).
Для нормального распределения эти коэффициенты должны быть близки нулю. Но, поскольку они являются выборочными, то на практике точное равенство нулю почти не встречается. Поэтому для проверки нормальности распределения рекомендуется использовать соответствующие таблицы (Приложение), в которых указаны критические точки для этих коэффициентов при различных уровнях значимости и объемах выборки. · Если оба рассчитанные значение для ассиметрии и эксцесса по модулю меньше этих критическихточек, гипотеза о нормальности распределения принимается. · Если хотя бы один коэффициент больше критического значения, то распределение отличается от нормального Пример. Проверить на нормальность распределения систолического артериального давления по выборке из 25 значений. Н(0): распределение систолического давления соответствует нормальному распределению Выполним вычисления
Поскольку вычисленные значения коэффициентов по модулю меньше соответствующих табличных (см. Приложение), то принимается нулевая гипотеза, т.е. распределение соответствует нормальному. Контрольные вопросы 1. Чтопонимаетсяподтермином«распределение» 2. Классификацияпризнаков, ккакимпризнакамприменимопонятиераспределение 3. Чтохарактеризуюткоэффициентассиметрииикоэффициентэксцесса. 4. Какимисвойствамиобладаетнормальноераспределение 5. Какпроверитьнормальностьраспределения Задание к СРСП 2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 688; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.58 (0.009 с.) |


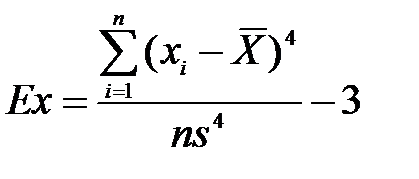
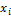



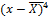
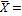 127
127

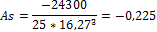

 127
127



