
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 1. Статистические методы анализа групповых свойств биологических объектовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ по БИОСТАТИТИКЕ Оглавление РАЗДЕЛ 1. СТАТИСТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ГРУППОВЫХ СВОЙСТВ БИОЛОГИЧЕСКИХ ОБЪЕКТОВ.. 3 Практическое занятие 1: Построение и описание гистограмм.. 3 СРСП 1. Вычисление статистических характеристик случайных величин. 9 СРСП 2. Проверка гипотезы о нормальности распределения случайной величины. 15 РАЗДЕЛ 2. ТЕОРИЯ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ. 20 Практическое занятие 2.Критерий Стьюдента для анализа биомедицинских данных. Доверительный интервал. 20 Практическое занятие 3.Непараметрические критерии проверки статистических гипотез. 26 СРС 1. Определение минимального объема выборки. 27 РАЗДЕЛ 3. АНАЛИЗ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН.. 28 СРСП 3.Сравнение относительных величин. 28 СРСП 4. Анализ качественных признаков. Таблицы сопряженности. 32 СРС 2. Оценка рисков и шансов. Оценка специфичности, чувствительности и прогностической значимости диагностических тестов. 35 РАЗДЕЛ 4. МЕТОДЫ ПРОГНОЗИРОВАНИЯ.. 36 Практическое занятие 4. Линейная корреляция. Ранговый коэффициент корреляции Спирмена. 36 Практическое занятие 5. Метод анализа выживаемости. 39 СРСП 5. Прогнозирование на основе линейной регрессии. 41 СРСП 6: Прогнозирование на основе кривой выживаемости. 44 СРС 3. Прогнозирование на основе среднего абсолютного прироста. 45 РАЗДЕЛ 5. 46 Практическое занятие 6. Дисперсионный анализ. Метод однофакторного дисперсионного анализа. 46 СРСП 7.Анализ научной публикации. 50 ПРИЛОЖЕНИЯ.. 51 Критические значения коэффициента асимметрии As. 51 Критические точки двустороннего t-критерия Стьюдента. 51 Критические значения χ2 53 Критические значения U-критерия Манна-Уитни, α = 0,01. Двусторонний критерий. 54 Критические значения парного Т-критерия Уилкоксона. 55 Таблица критических значений коэффициента корреляции рангов Спирмена. 56 Критические значения F-критерияФишера. 57 Примерный вариант заданий к рубежному контролю.. 60 Формулы подсчета статистических показателей. 62
РАЗДЕЛ 1. СТАТИСТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ГРУППОВЫХ СВОЙСТВ БИОЛОГИЧЕСКИХ ОБЪЕКТОВ
Практическое занятие 1: Построение и описание гистограмм Одним из способов представления и анализа случайных величин является построение гистограмм распределения. Гистограмма показывает, как часто встречаются те или иные значения случайной величины, по ней можно качественно оценить функцию плотности распределения. Рассмотрим правило построения гистограмм на конкретном примере. Работа с преподавателем. Задача: Даны значения пульса у 25 испытуемых (объем выборки n=25). Представить выборку в виде таблицы частот и построить гистограмму.
Необходимо выполнить следующие шаги: 1. Элементы выборки объемом n =25 расположить в ранжированный ряд (по возрастанию или убыванию)
2. Вычислить размах R (разность между минимальным и максимальным значением случайной величины): R=xmax-xmin=
3. Разбить вариационный ряд на k непересекающихся интервалов. k вычисляют по формуле Стерднесса, предусматривающей выделение оптимального числа интервалов: k=1+3.322lg(n) (округлить до целого) Можно воспользоваться следующими рекомендациями
4. Определить длину одного интервала: b=R/k
5. Определить границы каждого интервала 6. Определить частоты - количество ni элементов выборки, попавших в i-й интервал (элемент, совпадающий с правой границей интервала, относится к последующему интервалу) Наряду с частотами одновременно подсчитываются также относительные частоты
Полученные результаты сводятся в таблицу, называемую таблицей частот группированной выборки. Для нашей задачи результаты группировки представлены в следующей таблице:
7. Далее строится гистограмма. По оси абсцисс откладываются интервалы, по оси ординат могут откладываться абсолютная частота встречаемости, или относительная частота встречаемости, или же процент относительно общего объема выборки. В данном случае исследуемый признак – это пульс, который является случайной величиной X (x1, x2, x3 …..xi…… xn)
Этот график дает нам информацию о законе распределения случайной величины и носит название гистограммы распределения. Он показывает, насколько часто встречаются те или иные значения случайной величины. По оси ординат могут откладываться • Абсолютная частота встречаемости • Процент относительно общего объема выборки
• Относительная частота встречаемости
Огибающая гистограммы дает нам качественное представление о законе распределения случайной величины (иногда просто говорят распределение). Этот закон характеризует вероятность того, что случайная величина примет то или иное значение. Существует множество различных законов распределения. Наиболее распространенным является нормальное распределение – оно имеет симметричный колоколообразный вид. Какую информацию дает нам этот график. Самостоятельная работа: Согласно своему вариантудля случайной величины из таблицы данных построить гистограмму распределения. Описать полученные результаты.
Задание к ТЕМЕ 1 Опишите приведенную ниже гистограмму с указанием: · общего количестваобследованных. · минимального и максимального значения анализируемой величины, (с указанием в скольких процентов случаев) · наиболее часто и редко встречающегося значения анализируемой величины (с указанием в скольких процентов случаев) · в каких пределах в основном лежит анализируемая величина. · дайте качественную оценку функции плотности распределения данной случайной величины (нормальное или отличное от нормального).
 
 
 
 
Контрольные вопросы 1. Основные задачи биостатистики 2. Какую информацию несет гистограмма 3. Что понимается под термином «распределение» 4. Какая величина откладывается по оси ординат при построении гистограммы 5. Какая величина откладывается по оси абсцисс при построении гистограммы 6. Как определяется число интервалов при построении гистограммы 7. Какими свойствами обладает нормальное распределение 8. В каком случае две совокупности считаются не отличающимися по данному признаку 9. При каких условиях две нормально распределенные совокупности не отличаются по данному признаку.
Дидактический блок
Стандартное отклонение (среднеквадратичное отклонение) –также является характеристикой разброса, введена для того, чтобы избавиться от квадрата единицы измерения
Коэффициент вариации представляет собой относительную меру разброса, выраженную в процентах. Он вычисляется по формуле:
Коэффициент вариации: · используют для сравнения разброса двух и более признаков, имеющих различные единицы измерения. · он позволяет судить об однородности совокупности: 17% – абсолютно однородная; 17–33% – достаточно однородная; 35–40% – недостаточно однородная; 40–60% – это говорит о большомразбросе совокупности. Т.е. считаем выборку однородной при V% ≤ 33%
Стандартная ошибка средней. Так как среднее значение, как правило, определяется по ограниченной выборке, а не по генеральной совокупности, то оно отличается от истинной (генеральной) средней, то есть имеет определенную ошибку, называемой стандартнойошибкой средней
Мода (Мо) – наиболее часто встречающееся значение случайной величины. Для того, чтобы определить моду все значения выборки выстраиваются в ранжированный ряд (по возрастанию или по убыванию). Может быть несколько значений моды. По ранжированному ряду находим и медиану (Ме) – это значение случайной величины, которое делит выборку на две равные части. Если число объектов выборки четное, то медиана равна среднему двух соседних значений. Нижний квартиль Q25 – это значение случайной величины, ниже которого находится 25% выборки. В ранжированном ряду нижний квартиль находится под номером, определяемым по формуле:
(округлить до ближайшего) Верхний квартиль Q75 – это значение случайной величины, выше которого находится 25% выборки. В ранжированном ряду верхний квартиль находится под номером, определяемым по формуле:
(округлить до ближайшего) Межквартильный (интерквартильный) размах – это разница ΔQ=Q75-Q25. 50 % данных лежит в пределах от нижнего до верхнего квартилей. Пример расчета
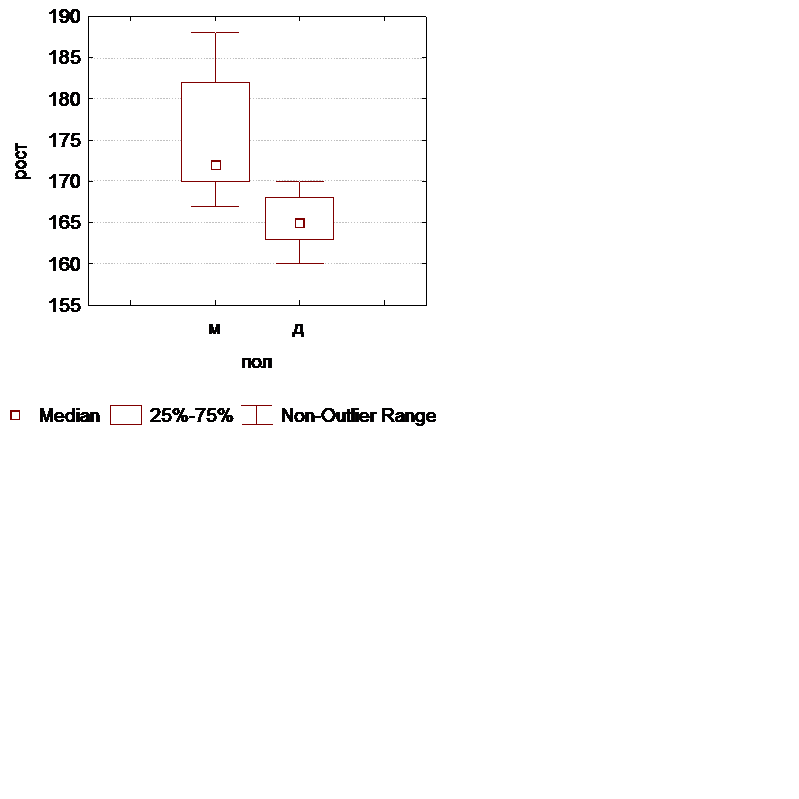
Анализ результатов:
У девочек группа более однородная, т.е. они не сильно различаются по росту.
Контрольные вопросы: Задание к СРСП 2. Работа с преподавателем Работа с преподавателем. Задача. В группе здоровых людей и больных гепатитом было определено содержание белка в сыворотке крови (Таблица 1). Определить, отличаются ли средние значениябелка в двух г енеральных совокупностях, если известно, что белок распределен по нормальному закону и генеральные дисперсии обеих совокупностей равны. Таблица 1.
Решение: Н(0): Н(1):
Вычислим средние значения для двух выборок: Для следующих вычислений составим таблицу
Вычислим среднее квадратическое отклонение для выборок:
Найдем стандартные ошибки:
Рассчитаем t-критерий:
Определим число степеней свободы в двух группах: f = (n+n2- 2 )= Определимпо таблицедвусторонний критерий tкрит для α=0,05 tкрит = Вывод: Сведем результаты расчетов в таблицу и представим графически
Найдем доверительный интервал для разницы средних
СЛУЧАЙ 2. Выборки зависимы. Для сравнения двух зависимых выборок или выборок с попарно связанными вариантами проверяют гипотезу о равенстве нулю среднего значения их попарных разностей. Такая задача возникает, когда имеются данные об изменении интересующего признака у каждого пациента. Например, если группа пациентов получала изучаемый метод лечения и у каждого пациента измерялось значение признака до и после лечения. В данном случае предстоит проверить нулевую гипотезу о равенстве нулю среднего изменения этого признака в результате получения терапии. При подобных исследованиях все наблюдения можно представить в виде n -пар измерений (например, до и после) Для каждой пары вычисляется разность di, i=1, n Для полученного ряда вычисляется среднее
Критерий Стъюдента определяется по формуле
tкрит находится по таблице для заданного α и числа степеней свободы f=n- 1
Если │tвыч │<tкрит то Н(0)
Если │tвыч│≥tкрит то Н(1) и делается заключение о наличии статистически значимых различий между средними значениями «до» и «после» на соответствующем уровне значимости. · Доверительный интервал для разницы генеральных средних двух зависимых групп лежит в пределах от
где t – критическое значение двустороннего t -критерия Стъюдента для заданного α и (п -1) степеней свободы. Работа с преподавателем. В группе из 6 больных гипертонией изучалось влияние лекарственного препарата, снижающего артериальное давление. В результате опыта получилось 2 вариационных ряда систолического давления: первый – до приема препарата, второй – после приема: Таблица 1.
Определить, изменяется лив генеральной совокупностисистолическое артериальное давление после приема препарата и насколько статистически значимы полученные результаты, если известно,что данные имеют нормальное распределение и две генеральные дисперсии равны? Для наглядности представим данные в следующей таблице: Таблица 2.
Н(0): Н(1):
Для разностей давлений:
Определим tвыч:
Определим по таблице Стьюдента tкрит для α=0,05 и числа степеней свободы f=n-1= tкрит= (двусторонний критерий). Вывод:
Сведем результаты расчетов в таблицу
Определим доверительный интервал для средней разницы двух зависимых групп. .
Контрольные вопросы 1. Основные задачи биостатистики 2. Генеральная совокупность и выборка. Какие бывают выборки. 3. Понятие распределения, нормальное распределение и его свойства 4. В каком случае две совокупности считаются не отличающимися по данному признаку 5. При каких условиях две нормально распределенные совокупности не отличаются по данному признаку. 6. Понятие статистических гипотез 7. Как проверяются гипотезы 8. Уровень значимости и достигнутый уровень значимости 9. Виды критериев, как выбрать критерий 10. Какие гипотезы проверяются при помощи критерия Стъюдента 11. Понятие доверительного интервала 12. Интерпретация доверительного интервала
Контрольное задание: СЛУЧАЙ 2. Выборки зависимые В случае попарно связанных выборок применяется Т-критерий Уилкоксона. При этом: · Вычисляются попарные разницы значений до и после · Попарные разницы, кроме нулевых, без учета знака ранжируются в один ряд · Разницам, кроме нулевых, присваиваются ранги, при чем одинаковым по модулю величинам присваивают одинаковый ранг · Отдельно вычисляют сумму рангов положительных (Т+) и отрицательных разностей (Т-), · Меньшую из двух таких сумм без учета знака выбирают в качестве критерия · Если Твыч>Ткритто Н(0) · Если Твыч≤ Ткритто Н(1)
Работа с преподавателем Стояла задача определить влияет ли препарат «Биоконт» на содержание белка в плазме крови. С этой целью препарат был испытан на десяти кроликах. Результаты эксперимента приведены в таблице.
Выдвигаем нулевую гипотезу:
В качестве критерия выбираем меньшее значение Твыч = Табличное значение для уровня значимости 0,05 и числа пар наблюдений п = (двусторонний критерий): Ткрит= Вывод:
Контрольные вопросы 1. Основные задачи биостатистики 2. Генеральная совокупность и выборка. Какие бывают выборки. 3. Понятие распределения, нормальное распределение и его свойства 4. В каком случае две совокупности считаются не отличающимися по данному признаку 5. Понятие статистических гипотез 6. Как проверяются гипотезы 7. Уровень значимости и достигнутый уровень значимости 8. Виды критериев, как выбрать критерий Контрольное задание: В контрольных задачах к Практическому занятию 2 проверить гипотезу о принадлежности двух выборок одной генеральной совокупности с использованием непараметрических критериев. Обосновать выбор критерия. Сформулировать нулевую и альтернативную гипотезы. Сделать выводы на уровне значимости a=0,01 или a=0,05 Задание к СРСП 3 1. Сравните относительную частоту встречаемости признака в двух совокупностях, используя критерий Стъюдента. 2. Сформулируйте нулевую и альтернативную гипотезы. 3. Определите доверительный интервал для доли в каждой группе 4. Определите доверительный интервал для разности этих долей. 5. Дайте интерпретацию доверительного интервала. 6. Сделайте выводы на уровне значимости 0,05 7. Результаты сведите в таблицу
Вариант 1 Исследовалась заболеваемость в сельской и городской местности. Выборочные исследования показали, что в селе из ста жителей обращались к врачу 36 человека, в городе из 100 жителей посетили врача 28 человек. Определить зависит ли обращаемость к врачу от места жительства.
Вариант 2. В случайной выборке из 150 одиноких лиц количество холостых мужчин составило 72, а незамужних женщин –78 человек. На основании этих данных сделайте вывод о теоретической возможности всех незамужних женщин в генеральной совокупности одиноких людей выйти замуж.
Вариант 3 Сравнивалась эффективность двух методов лечения и получены следующие данные
Отличаются ли по эффективности эти два вида лечения? Сформулируйте нулевую гипотезу. Сделайте вывод на уровне значимости 0,05.
Вариант 4 На экзамене по биостатистике билет состоял из вопросов из двух разных разделов. Экзамен сдавало 20 студентов специальности «общая медицина». Оказалось, что из первого раздела попались 22 вопроса, из второго раздела - 18.Соотносятся ли эти данные с предположением, что при проведении экзамена в генеральной совокупности студентов вопросы из обоих разделов попадаются с равной вероятностью. Сформулируйте нулевую гипотезу. Сделайте вывод на уровне значимости 0,05. Вариант 5 1000 человек классифицировали по признаку дальтонизма. По приведенным ниже данным проверить, есть ли зависимость между наличием дальтонизма и полом человека, при α = 0,05. Сформулируйте нулевую гипотезу.
Вариант 6 Во время эпидемии гриппа изучалась эффективность прививок против этого заболевания. Получены следующие результаты:
Указывают ли эти результаты на эффективность прививок? Сформулируйте нулевую гипотезу. Принять α = 0,05. Вариант 7 На предприятии химической промышленности, где работает 1400 человек, заболеваемость составила 37%, в то время как в целом в данном регионе она регистрируется на уровне 23% (в регионе проживает 15000 чел.). Влияют ли условия предприятия на заболеваемость? Сформулируйте нулевую гипотезу. Сделайте вывод на уровне значимости 0,05.
Вариант 8 Данные социологического исследования показали, что среди молодежи спортом занимаются 42 человека из 200 опрошенных, среди лиц старшего возраста – 55 из 325 опрошенных. Определите, есть ли зависимость увлеченности спортом от возраста. Сформулируйте нулевую гипотезу. Сделайте вывод на уровне значимости 0,05.
Вариант9. Среди 84 подземных рабочих хронический бронхит регистрируется у четверти, у строителей он диагностирован у трети из 105 обследованных. Определить влияет ли профессия на риск возникновения хронического бронхита. У кого эта вероятность выше? Сформулируйте нулевую гипотезу. Сделайте вывод на уровне значимости 0,05.
Вариант 10. 500 человек классифицировали по признаку аллергии к полыни. По приведенным ниже данным проверить, есть ли зависимость между наличием аллергии и полом человека, при α = 0,05.
Вариант 11 Сравнивалась эффективность двух антибиотиков и получены следующие данные
Отличаются ли по эффективности эти два антибиотика? Сформулируйте нулевую гипотезу. Сделайте вывод на уровне значимости 0,05. Вариант 12. После первого год
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 и процент случаев относительно общего объема выборки
и процент случаев относительно общего объема выборки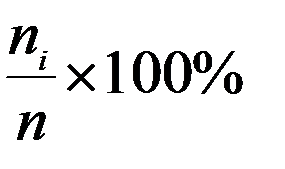




 Среднее значение (
Среднее значение ( ) – характеристика положения значений случайной величины на оси измерений
) – характеристика положения значений случайной величины на оси измерений Дисперсия (D) – характеристика разброса значений случайной величины относительно среднего значения
Дисперсия (D) – характеристика разброса значений случайной величины относительно среднего значения
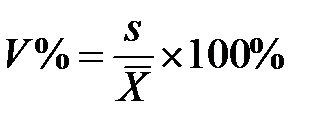







 =165,3
=165,3













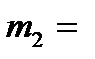

 (г/л)
(г/л)

 и среднеквадратичное отклонение
и среднеквадратичное отклонение  , стандартную ошибку средней
, стандартную ошибку средней 

 до
до 



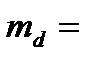

 (мм.рт.ст.)
(мм.рт.ст.)
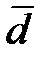 (мм.рт.ст.)
(мм.рт.ст.)



