
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По данным из таблицы построить гистограмму распределения, провести эмпирическую кривую распределения, вычислить коэффициенты ассиметрии и эксцесса, проверить гипотезу о нормальности распределения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Алгоритм подбора критериев при сравнении двух выборок
РАЗДЕЛ 2. ТЕОРИЯ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Практическое занятие 2.Критерий Стьюдента для анализа биомедицинских данных. Доверительный интервал Наиболее распространенным параметрическим критерием оценки различий между сравниваемыми генеральнымисредними значениями является критерий Стьюдента, или t-критерий. Нулевая гипотеза заключается в равенстве генеральных средних или, другими словами, проверяется нулевая гипотеза о принадлежности двух сравниваемых выборок одной и той же генеральной совокупности.
Работа с преподавателем СЛУЧАЙ 1. Выборки независимы. Проверяемый t-критерий вычисляется по формуле
где m1, m2 — стандартные ошибки средних значений сравниваемых выборок.
tкрит находится по таблице для заданного α и числа степеней свободы f =n1 + n2 – 2
Если │tвыч │<tкрит то Н(0)
Если │tвыч│≥tкрит то Н(1) и делается заключение о наличии статистически значимых различий между генеральными средними значениями на соответствующем уровне значимости.
· Доверительный интервал генеральной средней Генеральное среднее значение с вероятностью 95% лежит в пределах
от где t – табличное значение критерия Стъюдента для α =0,05 и f=n-1
· Доверительный интервал для разницы генеральных средних двух независимых групп Чтобы найти доверительный интервал для генеральной разности сначала надо вычислить объединенное среднеквадратичное отклонение:
Тогда доверительный интервал составляет от
где t – критическое значение двустороннего t -критерия Стъюдента для заданного α и f= (п1+п2 - 2) степеней свободы.
Работа с преподавателем. Задача. В группе здоровых людей и больных гепатитом было определено содержание белка в сыворотке крови (Таблица 1). Определить, отличаются ли средние значениябелка в двух г енеральных совокупностях, если известно, что белок распределен по нормальному закону и генеральные дисперсии обеих совокупностей равны. Таблица 1.
Решение: Н(0): Н(1):
Вычислим средние значения для двух выборок: Для следующих вычислений составим таблицу
Вычислим среднее квадратическое отклонение для выборок:
Найдем стандартные ошибки:
Рассчитаем t-критерий:
Определим число степеней свободы в двух группах: f = (n+n2- 2 )= Определимпо таблицедвусторонний критерий tкрит для α=0,05 tкрит = Вывод: Сведем результаты расчетов в таблицу и представим графически
Найдем доверительный интервал для разницы средних
СЛУЧАЙ 2. Выборки зависимы. Для сравнения двух зависимых выборок или выборок с попарно связанными вариантами проверяют гипотезу о равенстве нулю среднего значения их попарных разностей. Такая задача возникает, когда имеются данные об изменении интересующего признака у каждого пациента. Например, если группа пациентов получала изучаемый метод лечения и у каждого пациента измерялось значение признака до и после лечения. В данном случае предстоит проверить нулевую гипотезу о равенстве нулю среднего изменения этого признака в результате получения терапии. При подобных исследованиях все наблюдения можно представить в виде n -пар измерений (например, до и после) Для каждой пары вычисляется разность di, i=1, n Для полученного ряда вычисляется среднее
Критерий Стъюдента определяется по формуле
tкрит находится по таблице для заданного α и числа степеней свободы f=n- 1
Если │tвыч │<tкрит то Н(0)
Если │tвыч│≥tкрит то Н(1) и делается заключение о наличии статистически значимых различий между средними значениями «до» и «после» на соответствующем уровне значимости. · Доверительный интервал для разницы генеральных средних двух зависимых групп лежит в пределах от
где t – критическое значение двустороннего t -критерия Стъюдента для заданного α и (п -1) степеней свободы. Работа с преподавателем. В группе из 6 больных гипертонией изучалось влияние лекарственного препарата, снижающего артериальное давление. В результате опыта получилось 2 вариационных ряда систолического давления: первый – до приема препарата, второй – после приема: Таблица 1.
Определить, изменяется лив генеральной совокупностисистолическое артериальное давление после приема препарата и насколько статистически значимы полученные результаты, если известно,что данные имеют нормальное распределение и две генеральные дисперсии равны? Для наглядности представим данные в следующей таблице: Таблица 2.
Н(0): Н(1):
Для разностей давлений:
Определим tвыч:
Определим по таблице Стьюдента tкрит для α=0,05 и числа степеней свободы f=n-1= tкрит= (двусторонний критерий). Вывод:
Сведем результаты расчетов в таблицу
Определим доверительный интервал для средней разницы двух зависимых групп. .
Контрольные вопросы 1. Основные задачи биостатистики 2. Генеральная совокупность и выборка. Какие бывают выборки. 3. Понятие распределения, нормальное распределение и его свойства 4. В каком случае две совокупности считаются не отличающимися по данному признаку 5. При каких условиях две нормально распределенные совокупности не отличаются по данному признаку. 6. Понятие статистических гипотез 7. Как проверяются гипотезы 8. Уровень значимости и достигнутый уровень значимости 9. Виды критериев, как выбрать критерий 10. Какие гипотезы проверяются при помощи критерия Стъюдента 11. Понятие доверительного интервала 12. Интерпретация доверительного интервала
Контрольное задание:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 832; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 до
до  ,
,
 до
до 













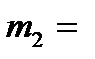

 (г/л)
(г/л)

 и среднеквадратичное отклонение
и среднеквадратичное отклонение  , стандартную ошибку средней
, стандартную ошибку средней 

 до
до 



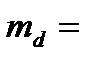

 (мм.рт.ст.)
(мм.рт.ст.)
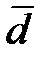 (мм.рт.ст.)
(мм.рт.ст.)



