
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система анализа маркетинговой информацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Система анализа маркетинговой информации представляет набор совершенных методов анализа. В основу любой системы анализа маркетинговой информации положен статистический банк и банк моделей. Статистический банк – совокупность современных методик статистической обработки информации, позволяющих наиболее полно вскрыть взаимозависимости данных и установить степень их статистической надежности. Банк моделей – набор математических моделей, способствующих принятию более оптимальных маркетинговых решений по деятельности рынка. Каждая модель состоит из совокупности взаимосвязанных переменных, представляющих некую реально существующую систему, процесс или результат. Эти модели могут дать ответы на вопросы типа: Система анализа маркетинговой информации представлена в виде схемы (рис.3.4.)
ris 013 Рис. 3.4. Система анализа маркетинговой информации.
Одномерный анализ. Двухмерный анализ
53. Дисперисионный анализ – стат метод анализа м инф, кот исп для изучения разл средних значений зависимых переменных, вызванных влиянием контролируемых и независимых переменных, при условии, что учтено вляиние неконтролир независ переменных. К статистиам, исп в дисп анализе, относ.:1.эта –квадрат ( ) –корреляционное отношение. С его пом выражают степень влияния и силу эффекта Х(независ переменной или переменных) на У (зависимую переменную). Значение лежит в интервале от0до 1.2.F- критерий (F-статистика) – отношение межгрупповой дисперсии к дисперсии ошибки, с помощью которого проверяют равенство категориальных средних в выборочных совокупностях;3.MS, средний квадрат – сумма квадратов отклонений, поделенная на соотв ей число степеней свободы;4. ) –корреляционное отношение. С его пом выражают степень влияния и силу эффекта Х(независ переменной или переменных) на У (зависимую переменную). Значение лежит в интервале от0до 1.2.F- критерий (F-статистика) – отношение межгрупповой дисперсии к дисперсии ошибки, с помощью которого проверяют равенство категориальных средних в выборочных совокупностях;3.MS, средний квадрат – сумма квадратов отклонений, поделенная на соотв ей число степеней свободы;4. 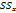 , вариация переменной У, обусловленная различиями между группами;5. , вариация переменной У, обусловленная различиями между группами;5.  ,,вариаця переменной У, обусловленная вариацией внутри каждой группы категорий – вариация переменной у, обусловленная изменением внутри каждой из групп пременной Х;6.общая сумма квадратов ,,вариаця переменной У, обусловленная вариацией внутри каждой группы категорий – вариация переменной у, обусловленная изменением внутри каждой из групп пременной Х;6.общая сумма квадратов  , - полная дисперсия переменной У Процедура выполнения дисперсионного и коварационного анализа:1).определение зависимой и независимой переменной,2).выбор метода разложения дисперсии,3).разложение полной диспеерсии,4).измерение эффектов,5).проверка значимости,6).интерпретеция полученных результатов. 1.пусть У – зависимая переменная, а Хі – независимая переменная, имеющая К – категорий.для каждой руппы Хі – существует n- наблюдеий У. 2.метод разложения дисперсии зависит от количества и типа используемых переменных.1.Зависимая маетрическая переменная (измеренная с помощью интервальной или относительной шкалы) →одновакторный дисперсионный анализ.2.две или более независимые переменные:2.1.две или более категориальные независимые переменные (измеренные с помощью порядковой или номинальной шкалы)→многофакторный дисперсионный анализ.2.2.одна или более категориальные независимые меременные (фаторы) и одна или более метрические независимые переменные (коварианты)→коварационный анализ 3.для изучения различий между средними величинами дисперсионный анализ использует разложение полной вариации, наблюдаемой в зависимой переменной. Полную вариацию (SS) в однофакторном дисперсионном анализе можно разложить на два комонента , - полная дисперсия переменной У Процедура выполнения дисперсионного и коварационного анализа:1).определение зависимой и независимой переменной,2).выбор метода разложения дисперсии,3).разложение полной диспеерсии,4).измерение эффектов,5).проверка значимости,6).интерпретеция полученных результатов. 1.пусть У – зависимая переменная, а Хі – независимая переменная, имеющая К – категорий.для каждой руппы Хі – существует n- наблюдеий У. 2.метод разложения дисперсии зависит от количества и типа используемых переменных.1.Зависимая маетрическая переменная (измеренная с помощью интервальной или относительной шкалы) →одновакторный дисперсионный анализ.2.две или более независимые переменные:2.1.две или более категориальные независимые переменные (измеренные с помощью порядковой или номинальной шкалы)→многофакторный дисперсионный анализ.2.2.одна или более категориальные независимые меременные (фаторы) и одна или более метрические независимые переменные (коварианты)→коварационный анализ 3.для изучения различий между средними величинами дисперсионный анализ использует разложение полной вариации, наблюдаемой в зависимой переменной. Полную вариацию (SS) в однофакторном дисперсионном анализе можно разложить на два комонента  = = 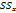 + + 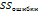 Полная вариация представляет вариацию между категориальной переменной Х. Полная вариация представляет вариацию между категориальной переменной Х. 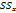 - доля в сумме квадратов переменной У, обусловленная действием независимой переменной или фактором Х. - доля в сумме квадратов переменной У, обусловленная действием независимой переменной или фактором Х. 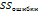 - вариация переменной У, связанная с вариацией внутри каждой группы переменной Х, ее вычисляют, не учитывая фактор Х: - вариация переменной У, связанная с вариацией внутри каждой группы переменной Х, ее вычисляют, не учитывая фактор Х:  4.в однофакторном дисперсионном анализе сила влияния переменной Х на У измеряется с помощью
Значение корреляционного отношения лежит в пределах от0 до 1. Значение =1, когда внутри каждой из групп переменной Х изменчивость отсутствует, но имеется некотороая изменчивость между группами. При многофакторном дисп. Анализе эффект влияния опред с помощью множественной корреляции. Множественная корреляция – степень объединенного вляниядвух или более факторов или полный эффект
5.проверка значимости. В однофакторном дисп анализе проверяют нулевую гипотезу, утверждающую, что групповые средние в рассчитываемой совокупности равны. В соответствии с нулевой гипотезой значения
Нулевую гипотезу можно проверить с помощью F – статистики, рассчитываемой как отношение между этими двумя отношениями дисперсий
В многофакторном дисперсионном анализе проверку значимости осуществляют путем оценки значимости полного эффекта
Если полный эффект статистически значимый, то на след этапе изучают значимость эффекта. Если нулевая гипотеза утверждает, что взаимодействие между фактороамиотсутствует, то соотв F – критерийвычис по формуле
Если окажется, что эффект взаимодействия статистики значисый, то эффект Х1 зависит от Х2 и наоборот. Поскольку эффект одного фактора неоднародный, а зависит от уровня другого фактора, то бессмысленно проверять значимость этих гл эффектов. Однако целесообр проверить значимость гл эффекта каждого фактора, если эффект воздействия статистически незначимый. В таком случае проерка значимости гл эффекта для каждого отд фактора произв след образом: 6.если нулевую гипотезу о равенстве групповых средних не отклоняют, то независисмые переменные не оказывают статистическо значимого влиянияна зависимую переменную.
54. дискриманационный анализ – анализ различий заранее заданных групп объектов исследования. Премепнная, разделяющая совокупности объектов исследования на группы, назыв группирующей. С помощью дискриминационного анализа изуч различия между двумя или более группаи по оперд признакам. Признаки, используемые для выявления различий между двумя и более группами – дискриминационные переменные. Группирующая (зависимая) переменная:
Статистикаи, используемые в дискриминационном анализе: 1)каноническая корреляция – измеряет степень связи между дискриминпционными покахателями и группами. 2)центроид (средняя точка) – среднее занчения для дискриминантных показателей конкретной группы. 3)классификационная матрица (смешанная или матрица предсказаний) – содержит ряд правильно и ошибочно классифицированных случаев. 4)коэф дискриминантной функции – коэф переменных, измеренные в первоначальных единицах; 5)дискриминационные показатели – сумма произведений ненормированных коэф дискриминац функции на значений переменных, добавленная к постоянному члену; 6)собственное (характеристическое) значение – отношение межгурупповой суммы квадратов к внутригрупповой сумме квадратов; 7)F – статистика и ее значимость. Значение F – статистики вычисляет однофакорный дисперсионный анализ, разбивая на группы независимую переменную; 8)средние группы и групповые стандартные отклонения – эти показатели вычисляют для каждого предиктора каждой группы; 9)объединенная межгупповая корреляционная матрица вычисляется устранением отд коварационных матриц для всех групп; 10)нормированные коэф дискриминантных функций. Коэф дискриминантных функций используют как множители для нормированных переменных, тет переменные с нулевым средним и дисперсией равной 1. 11)структурные коэф. корреляции (дискриминантные нагрузки) – линейные коэф корреляции между предикотрами и дискриминаниной функцией; 12)общая коррелционная матрица. Если при вычислении корреляции наблюдения обрабатывают так, как будто они взяты из одной выборки, то в результате получают общую корреляционную матрицу; 13)коэф лямбда (λ) Уилкса (U – статистика) – отношение внутри групповой суммы квадратов к общей сумме квадратов. Его значение варьируется от 0 до 1
Процедура выполнения дискриминационного анализа: 1.определение зависимой и независимой переменных, 2.выбор метода дискриминационного анализа, 3.Опред коэф дискриминационной функции, Функция f (x) наз канонической дискриминационной функцией, а величины Х1, Х2 – дискриминационными переменными
Дискриминантная ф-ция может быть линейной и нелинейной. Выбор зависит от геометрического расположения разделяемых классов в пространстве дискриминационных переменных. Коэф дискр ф-ций опред между собой таким образом, что бы f1 (x),f2(x)имели большие различия между собой. Вектор коэф дискриминнантной ф-ции А опред по формуле
Полученные значения коэф подст в формулу f (x) и для каждого объекта в обоих множествах вычисляют дискриминантные функции, затем наод среднее значение для каждой группы Необх опред границу раздел два множества. Такой величиной может быть значение ф-ции, равноудаленное от f1 и f2
Объекты расположенные над разделяющей поверхностью f (x) =а1х1+а2х2+…. =с, наод ближе к центру множества М1. Если граница между группами будет выбрана выше, то суммарная вероятность ошибочной классификации будет минимальной. 4.опред занчимой дискриминационной функции (с помощью программы SPSS), 5.интерпретация полученных результатов, 6.оценка достоверности дискриминационного анализа.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |


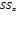 . Эффект влияния переменной Х на У опред по формуле
. Эффект влияния переменной Х на У опред по формуле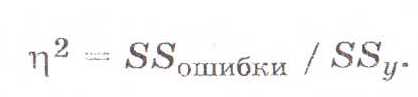
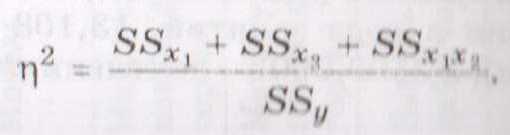
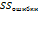 зависят от одного источника вариации. В таком случае оценка дисперсии совокупности У может опредмежгупповой или внутригрупповой вариацией.
зависят от одного источника вариации. В таком случае оценка дисперсии совокупности У может опредмежгупповой или внутригрупповой вариацией.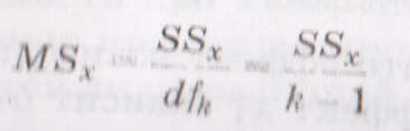 или
или 





 – коэф дискриминац функции;
– коэф дискриминац функции;  - свободный член 9константа);
- свободный член 9константа);  – дискриминационные (независимые) переменные.
– дискриминационные (независимые) переменные.


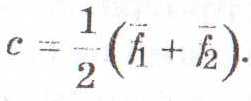 = константа дискриминации
= константа дискриминации


