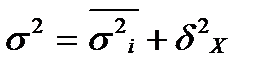Способы формирования выборочной совокупности

Существует 2 вида отбора:
1.Индивидуальный: случайный, механический, стратифицированный
2.Серийный

Помимо этого различают:
1.Комбинированный
2.Ступенчатый
3.Многфазный

Любой из этих видов отбора может быть повторный и бесповторный. По степени охвата единиц изучаемой совокупности выделяют малые и большие выборки. Случайный отбор осуществляется с помощью жеребьевки или по табл. случайных чисел. При механическом отборе выбираются n/N элемента, если единицы совокупности не ранжированы, то 1-й элемент выбирается наугад. Если ранжированный, то из середины 1-й 100-и. Принцип случайного отбора в механической выборке обеспечивается тем, что единицы ген. Совокупности располагаются в том порядке, который не оказывает влияния на поведение изучаемого признака.

 

Этапы формирования выборки

Процесс выборочного обследования включает след. этапы:

1)определение основы построения выборки. Основу для построения выборки составляют списки элементов генеральной совокупности или правила нахождения этих элементов. В качесте примеров правил нахождения элементов генеральной совокупности можно использовать таблицу семизначных чисел, сгенерированных случайным образом для использования при опросе тел номеров.

Способы коррекции:

1.пререраспределение генеральнрой совокупности, которая должна соответствовать основе выборки;

2.отсев лишних элементов выборки на стадии проведения опроса.

3.взвешивание (выравнивание) данных путем задания весовых коэффициентов.

2)устранение различий объектов выборки и генеральной совокупности.

Если основа выборки не совпадает с определеним совокупности, возникают три типа проблем:

1.проблема подмножества, если основа выборки меньше совокупности;

2.проблема супермножества, если основа выборки больше совокупности, однако при этом содержит все ее элементы;

3.проблема пересечения, если некоторые элементы совокупности отсутствуют в основе выборки, а сама основа выборки содержит больше элементов, нежели целевая совоукпность.

3)выбор процедуры формирования выборки. Выборочное обследование можно разделить на два вида: описательное и аналитическое. Цель описательного обследования состоит в получении сведений о некоторых больших группах. При аналитическом обследовании сравниваются различные подгруппы совокупности для того, чтобы установить, существуют ли между ними различия, которые позволили бы нам построить или проверить гипотезы о природе сил, действующих в данной совокупности.

Способы простроения выборки классиф по след основаниям:

1. фиксированные (традиционные) и последовательные (байесовские)

Фиксированные подразумевают априорное определегние их размера и получение информации только от выбранных элементов.

Последовательные – подразумевают возможность принятия дополнительных решений в ходе их формирования.

2.в зависимости от способа отбора единиц:

повторные (с возвращением)- вероятноть попадания каждой отдельной единицы в выборку остается постоянной;

бесповторные (без возвращения) – вероятность попадания отд единиц в выборку все время изменятся.

3. индивидуальные, групповые, комбинированные.

4. вероятностные (случайные) (каждый элемент исходной совокупности имеет изв ненулевую вероятность попадания в сосав выборки); детерминированные (неслучайные)

 

Формирование детеринированных выборок и оценка их репрезентативности.

В случае исп детерминированных выборок нет сопоба оценки вероятности того, что элемент исходной совоупности окажется включенным в состав выборки. Формирование всех невероятносных выборок основывается на личных суждениях. Хотя такие субъективные выборки могут отражать особенности исходной совокупности, ни не позволяют проводить объективную оценку адекватности проведенческого отбора элементов. Когда элементы совокупности выбираются с заранее изв вероятностью, появл возможность оценить точность результатов этого процесса.

 

Формирование простой случайной выборки.

Каждый элемент исследуемой совокупности имеет известную, одинаковую вероятность попадания в выборку. Изветсна и одинакова вреоятность того, что в результате отбора будет получен любой конкретный вариант выборки данного размера. Элементы извлекаются из основы выборки случайным оразом, независимо друг отдруга

 

Формирование стратифицированных выборок.

Стратифицированная или типическая выборка предст собой двухстаадийный процесс, в ходе которого множество элемнтов, образующих исследуемую совокупность, разделяется на подмножества, или мтраты, и каждый ее элемент входит тлько в одну страту. Затем в каждой страте отбир нужное число элементов. Формально для отбора в стратах должна исп процедура случайного отбора (SRS). На практике применяют систематический отбор ли др вероятностные процедуры. Основная цель стратификации – повысить точность без увеличения цены.

 

Формирование кластерных выборок.

При кластерной, генздовой или серийной выборке множество элементов, образующих, исследуемую совокупность, разделяются на попределенное число нерпесекающихся подмножеств, называемых кластерами. При использовании метода стратификации в выборку обязательно попадают представители всех страт. В данном случае производится случайный выбор кластеров, чьи элементызатем будут включатся в выборку. Если в выборку попадают все элементы выделенных кластеров, процедура наз одностадийной. Если из каждого кластера случайным образом извлекаются и включаются в выборку некотрые элементы, процедураназ двустадийной. Когда перед отбором отд элементов внутири выбранных из первой стадии кластеровсначала выделяют более мелкие, определенное число которых вновь отбирается случайными методами, то это трех- или более стадийная процедура. Кластеризация направлегна на экономию затрат без существенного снижения точности. Преимущества кластеризации: гибкость и невысокая стоимость.

 

Понятие дисперсии и среднего квадратического отклонения: генеральной совокупности, выбрки, выборочного среднего.

Дисперсия - средний квадрат отклонений индивидуальных значений признака от их средней величины.

Свойства дисперсии:

1. Дисперсия постоянной величины равна нулю.

2. Уменьшение всех значений признака на одну и ту же величину А не меняет величины дисперсии. Значит средний квадрат отклонений можно вычислить не по заданным значениям признака, а по отклонениям их от какого-то постоянного числа.

3. Уменьшение всех значений признака в k раз уменьшает дисперсию в k2 раз, а среднее квадратическое отклонение - к раз. Значит, все значения признака можно разделить на какое-то постоянное число (скажем, на величину интервала ряда), исчислить среднее квадратическое отклонение, а затем умножить его на постоянное число.

4. Если исчислить средний квадрат отклонений от любой величины А, то в той или иной степени отличающейся от средней арифметической (X~), то он всегда будет больше среднего квадрата отклонений, исчисленного от средней арифметической. Средний квадрат отклонений при этом будет больше на вполне определенную величину - на квадрат разности средней и этой условно взятой величины.

 

Внутригрупповая и межгрупповая дисперсия.

Выделяют дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия s2 измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

Межгрупповая дисперсия (s2x) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.

Внутригрупповая дисперсия (s2i) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.

 

Правило сложения дисперсий.

Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.

Правило сложения дисперсий широко применяется при исчислении показателей тесноты связей, в дисперсионном анализе, при оценке точности типической выборки и в ряде других случаев.

 

Среднее квадратическое отклонение определяется как корень из дисперсии.