Интервальные оценки случайной величины

Интервальной оценкой случайной величины называется множество точечных оценок, которые накрывают неизвестный параметр. Такой интервал называют доверительным интервалом (Рис. 1.10). Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака в нем. Величина интервала представляет собой разность между верхней и нижней границами интервала.

А б

Рис. 1.10

Если интервал расположен симметрично относительно центра нормального распределения (относительно математического ожидания а), так что влево и вправо взяты одинаковые отрезки ∆x (Рис. 1.10.б), то ширина интервала будет 2∆x. Иногда в решении задач доверительным интервалом называют полуширину ∆x. Границы интервала можно обозначить как α и β. Каждому доверительному интервалу ставится в соответствие доверительная вероятность Р или надежность. Эта оценка позволяет ответить на вопрос, какой вероятностью находится неизвестное значение оцениваемого параметра генеральной совокупности внутри заданного интервала.

И пусть мы не сможем точно указать, где на числовой оси находится неизвестный параметр, но мы можем указать доверительный интервал 2∆x, в котором он находится с доверительной вероятностью Р.

Функция Лапласа.

Для решения задачи интервального оценивания перейдем от переменной x к переменной t в функции Гаусса. Пусть (х–а) фактическое отклонение отдельного значения случайной величины от математического ожидания. Разделим его на стандартное отклонение σ. Обозначим результат деления как . Таким образом мы нормализуем или стандартизируем все значения переменной х. Данный параметр имеет следующий смысл: он показывает, во сколько раз фактическое отклонение отличается от стандартного. Поэтому параметр t называют относительным отклонением. Его принято называть статистическим критерием стандартного нормального распределения. При проверке статистических гипотез его значения позволяют или принять или отклонить выдвинутые гипотезы.

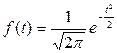Используя параметр t, можно произвести замену переменной в функции Гаусса . От этого выражение становится проще, а график сдвигается в начало координат в точку с координатой t=0 (с математическим ожиданием равным нулю и σ =1) с границами интервала – t и + t (Рис. 1.11). С таким графиком удобнее работать, так как множество различных случайных величин с нормальным распределением могут быть представлены однообразным графиком и появляется возможность создать единый алгоритм решения задач для самых разных СВ. Как уже было сказано выше, вероятность попадания значения случайных величин в заданный интервал равна площади под кривой функции плотности вероятности над данным интервалом. На Рис. 1.11 эта площадь заштрихована. В математике площадь, лежащая под графиком некоторой функции, равна интегралу от этой функции. Тогда для нахождения вероятности попадания значения случайных величин в интервал от – t до + t, проинтегрируем функцию плотности вероятности в данных пределах. 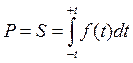. Учитывая симметричность интервала, найдем площадь от 0 до t и умножим на два. 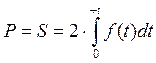. Подставим в данное выражение функцию Гаусса. .

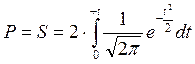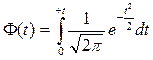Значения данного интеграла для разных t вычислил Лаплас и представил их в виде таблицы. Эту таблицу можно найти в любом математическом справочнике. Поскольку значения этого интеграла зависят от предела t, то интеграл от функции Гаусса стали называть функцией Лапласа и обозначать как . Таким образом, вероятность нахождения неизвестного значения оцениваемого параметра генеральной совокупности можно найти по формуле: Р=2Ф(t). Если интервал несимметричен P=Ф(t₂) – Ф(t₁)

Замечание. Иногда в таблицах нормального распределения вместо функции Лапласа указывается сама вероятность Р или уровень значимости α, параметр t может иметь обозначение z.

 

Рис. 1.11

 

Доверительный интервал для отдельных значений изучаемого признака при известном параметре σ

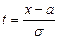Пусть генеральная совокупность Х распределена по нормальному закону N(a,σ), причем, параметр σ известен. Необходимо оценить доверительный интервал для самих значений измеряемого признака. В этом случае из формулы или 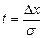выводим формулу доверительного интервала для отдельных значений СВ. Полуширина доверительного интервала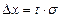

Его центр находится в точке a, левая граница имеет значение , правая граница 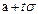, а длина интервала 2tσ.