
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целесообразность введения корреляционной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математическое ожидание и дисперсия характеризуют случайную функцию далеко не полно. Можно привести примеры двух случайных функций, которые имеют одинаковые математические ожидания и дисперсии, но поведение которых различно. Зная лишь эти две характеристики, в частности, ничего нельзя сказать о степени зависимости двух сечений. Для оценки этой зависимости вводят новую характеристику—корреляционную функцию. Далее покажем, что, зная корреляционную функцию, можно найти и дисперсию; поэтому знать закон распределения для отыскания дисперсии нет необходимости. Уже это обстоятельство указывает на целесообразность введения корреляционной функции. Прежде чем перейти к дальнейшему изложению, введем понятие центрированной случайной функции по аналогии с понятием центрированной случайной величины (центрированной случайной величиной называют разность между случайной величиной и ее математическим ожиданием: Центрированной случайной функцией называют разность между случайной функцией и ее математическим ожиданием:
Корреляционная функция случайной функции Рассмотрим случайную функцию Х (t). При двух фиксированных значениях аргумента, например при t= t 1и t= t 2, получим два сечения—систему двух случайных величин Х (t 1) и Х (t 2) с корреляционным моментом M [
Таким образом, каждая пара чисел t 1 и t 2 определяет систему двух случайных величин, а каждой такой системе соответствует ее корреляционный момент. Отсюда следует, что каждой паре фиксированных значений t 1 и t 2соответствует определенный корреляционный момент; это означает, что корреляционный момент случайной функции есть функция (неслучайная) двух независимых аргументов t 1 и t 2, ее обозначают через Кх (t 1, t 2). В частном случае значения обоих аргументов могут быть равны между собой. Приведем теперь определение корреляционной функции. Корреляционной функцией случайной функции Х (t)называют неслучайную функцию Кх (t 1, t 2) двух независимых аргументов t 1 и t 2, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов: Кх (t 1, t 2)= M [ Замечание. При равных между собой значенияхаргументов t 1= t 2 =t корреляционная функция случайной функцииравна дисперсии этой функции: Кх (t, t)= Dx (t) Действительно, учитывая, что Dx(t)=M[X(t)-mx(t)]2=M[ получим Кх (t, t)= M [ Таким образом, достаточно знать корреляционную функцию, чтобы найти дисперсию случайной функции. Пример. Задана случайная функция X (t) =Ut, где U —случайная величина, причем М (U)=4, D (U) = 10. Найти: а) корреляционную функцию; б) дисперсию заданной случайной функции. Р е ш е н и е. а) Найдем математическое ожидание: mx (t)= M [ X (t)]= M (Ut) =tM (U)=4 t Найдем центрированную функцию:
Отсюда
Найдем корреляционную функцию: Кх (t 1, t 2)= M [ Итак, искомая корреляционная функция Кх (t 1, t 2)= 10 t 1 t 2 б) Найдем дисперсию, для чего положим t 1 =t 2 =t; Dx (t) =Кх (t, t) = 10 tt. Итак, искомая дисперсия Dx(t)=10t2. Свойства корреляционной функции Свойство 1.При перестановке аргументов корреляционная функция не изменяется (свойство симметрии): Кх (t 1, t 2)= Кх (t 2, t 1). Доказательство. По определению корреляционной функции, Кх (t 1, t 2)= M [ Кх (t 2, t 1)= M [ Правые части этих равенств равны (математическое ожидание произведения не зависит от порядка сомножителей), следовательно, равны и левые части. Итак, Кх (t 1, t 2)= Кх (t 2, t 1). Замечание 1. Прибавление к случайной функции X (t} неслучайного слагаемого φ (t) не изменяет ее центрированной функции: Если Y (t) =Х (t) +φ (t), то
Действительно, математическое ожидание функции Y (t) my (t) =mx (t) +φ (t). Следовательно,
Итак,
Свойство 2.Прибавление к случайной функции Х (t) неслучайного слагаемого φ (t) не изменяет ее корреляционной функции: если Y (t) =X (t) +φ (t), то Кy (t 1, t 2)= Кх (t 1, t 2). Доказательство. В силу замечания 1
Отсюда M [ Итак, Кy (t 1, t 2)= Кх (t 1, t 2). Замечание 2. При умножении случайной функции Х (t) на неслучайный множитель φ (t) ее центрированная функция умножается на этот же множитель: если Y(t)=Х(t)+φ(t), то
Действительно, математическое ожидание функции Y (t) ту(t)=М[Х(t)φ(t)]=φ(t)mx(t). Следовательно,
Итак,
Свойство 3. Приумножении случайной функции Х (t) нанеслучайный множитель φ (t)еекорреляционная функция умножается на произведение φ (t 1) φ (t 2): Если
то Кy (t 1, t 2)= Кх (t 1, t 2) φ (t 1) φ (t 2). Доказательство. В силу замечания 2
Следовательно, Кy (t 1, t 2)= M [ Вынесем неслучайные множители за знак математического ожидания: Кy (t 1, t 2)= φ (t 1) φ (t 2) M [ Итак, Кy (t 1, t 2)= Kx (t 1, t 2) φ (t 1) φ (t 2) Свойство 4. Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений:
Доказательство. Известно, что для модуля корреляционного момента двух случайных величин справедливо неравенство (см. гл. XIV, § 17, теорема 2)
При фиксированных значениях аргументов t 1 и t 2 значение корреляционной функции равно корреляционному моменту соответствующих сечений—случайных величин Х (t 1) и Х (t 2). Поэтому неравенство (*) можно записать так:
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.180 (0.008 с.) |

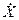 = Х - mx.
= Х - mx.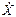 (t)]2,
(t)]2, (t)=
(t)= 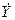 (t)=
(t)= 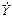 (t) =
(t) = 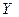 (t)=
(t)= 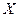 (t)φ(t).
(t)φ(t). .
.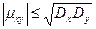 .
.


