
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия теорем сложения и умноженияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема сложения вероятностей совместных событий
Была рассмотрена теорема сложения для несовместных событий. Здесь будет изложена теорема сложения для совместных событий. Два события называют совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Пример 1. А — появление четырех очков при бросании игральной кости; В — появление четного числа очков. События А и В — совместные. Пусть события А и В совместны, причем даны вероятности этих событий и вероятность их совместного появления. Как найти вероятность события А + В, состоящего в том, что появится хотя бы одно из событий А и В? Ответ на этот вопрос дает теорема сложения вероятностей совместных событий. Теорема. Вероятность появления хотя бы одного из двухсовместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р (А + В) = Р (А) + Р (В) — Р (АВ). Доказательство. Поскольку события А и В, по условию, совместны, то событие А + В наступит, если наступит одно из следующих трех несовместных событий: A P (A+B) =P (A Событие А произойдет, если наступит одно из двух несовместных событий: Р (A) = Р (A Отсюда Р ( Аналогично имеем P (B) =P ( Отсюда Р ( Подставив (**) и (***) в (*), окончательно получим P (A+B) =P (A) +P (B) -P (AB). (****) Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий Р (А + B) = Р (А) + Р (В) -Р (А) Р (В); для зависимых событий Р (А + B) = Р (А) + Р (В) -Р (А) РA (В); Замечание 2. Если события А и В несовместны, то их совмещение есть невозможное событие и, следовательно, Р (АВ) =О. Формула (****) для несовместных событий принимает вид Р (А + B) = Р (А) + Р (В). Мы вновь получили теорему сложения для несовместных событий. Таким образом, формула (****) справедлива как для совместных, так и для несовместных событий. Пример 2. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: p 1= 0,7; p 2 = 0, 8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание) Р (АВ) =Р (А) Р (В) = 0, 7 * 0, 8 = 0, 56. Искомая вероятность Р (А+В) =Р (А) + Р (В) —Р (АВ) = 0, 7 + 0, 8 — 0, 56 = 0, 94. Замечание 3. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой Р== 1 —q 1 q 2(см. гл.III, §5). В самом деле, вероятности событий, противоположных событиям А и В, т. е. вероятности промахов, таковы: q 1 = 1 -p 1 = 1 — 0, 7 = 0, 3; q 2 = 1 —р 2 = 1 — 0, 8 = 0, 2. Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна P= 1 - q 1 q 2 = 1 - 0, 3 • 0. 2 = 0, 94. Как и следовало ожидать, получен тот же результат.
Формула полной вероятности Пусть событие А может наступить при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р (A) = Р (B 1) Эту формулу называют «формулой полной вероятности». Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий B 1 ,В 2 ,..., Вп. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В 1 А, В 2 А,..., ВпА, Пользуясь для вычисления вероятности события А теоремой сложения, получим P (A) =P (В 1 А) +P (В 2 А) +…+P (ВпА). (*) Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем Р (В 1 А) = Р (В 1) Р (ВnА) = Р (Вn) Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности P (A) = Р (В 1) Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго—0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) — стандартная.
Решение. Обозначим через А событие «извлеченная деталь стандартна». Деталь может быть извлечена либо из первого набора (событие В 1), либо из второго (событие В 2). Вероятность того, что деталь вынута из первого набора, Р (В 1) = 1 / 2. Вероятность того, что деталь вынута из второго набора, Р (В 2) = 1 / 2. Условная вероятность того, что из первого набора будет извлечена стандартная деталь, Условная вероятность того, что из второго набора будет извлечена стандартная деталь Искомая вероятность того, что извлеченная наудачу деталь — стандартная, по формуле полной вероятности равна Р (А) = Р (В 1) Пример 2. Впервой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке—10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной. Решение. Обозначим через А событие «из первой коробки извлечена стандартная лампа». Из второй коробки могла быть извлечена либо стандартная лампа (событие B 1), либо нестандартная (событие В 2). Вероятность того, что из второй коробки извлечена стандартная лампа, Р (В 1) = 9 / 10. Вероятность того, что из второй коробки извлечена нестандартная лампа, Р (В 2) = 1 / 10. Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа, равна Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа, равна Искомая вероятность того, что из первой коробки будет извлечена стандартная лампа, по формуле полной вероятности равна P (A) = Р (В 1)
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.91.245 (0.011 с.) |

 ,
, 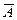 B или АВ. По теореме сложения вероятностей несовместных событий,
B или АВ. По теореме сложения вероятностей несовместных событий, (А),
(А),  (А) ,...,
(А) ,...,  (А)события А. Как найти вероятность события A? Ответ на этот вопрос дает следующая теорема.
(А)события А. Как найти вероятность события A? Ответ на этот вопрос дает следующая теорема. (А) +... +Р (Вп)
(А) +... +Р (Вп)  (А).
(А).


