
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка истинного значения измеряемой величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть производится п независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины Xl, Х 2,…, Хn. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии σ2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в двух предыдущих параграфах, выполняются, и, следовательно, мы вправе использовать полученные в них формулы. Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов. Поскольку обычно σ неизвестно, следует пользоваться формулами, приведенными в § 16. Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметической результатов отдельных измерений Решение. Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном σ) при помощи доверительного интервала
покрывающего а с заданной надежностью γ = 0,95. Пользуясь таблицей приложения 3, по γ = 0,95 и n = 9 находим tγ = 2,31. Найдем точность оценки:
Найдем доверительные границы:
Итак, с надежностью 0,95 истинное значение измеряемой величины заключено в доверительном интервале 38,469 < а < 46,169.
§ 18. Доверительные интервалы для оценки среднего квадратического отклонения σ нормального распределения
Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение σ по «исправленному» выборочному среднему квадратическому отклонению s. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр σ с заданной надежностью γ. Потребуем, чтобы выполнялось соотношение Р (|σ-s|<δ) = γ, или P (s-δ<σ<s+δ)= γ. Для того чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство s-δ<σ<s+δ в равносильное неравенство s (1 -δ/s) <σ<s (1 +δ/s). Положив δ/s = q, получим s (1 -q) <σ<s (1 +q). (*) Остается найти q. С этой целью введем в рассмотрение случайную величину «хи»:
где п - объем выборки. Как было указано [см. § 16, пояснение, соотношение (***)], величина S 2(n— 1) /σ 2распределена по закону χ2 с п- 1степенями свободы, поэтому квадратный корень из нее обозначают через χ.
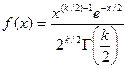
Плотность распределения χ имеет вид (см. пояснение в конце параграфа)
Это распределение не зависит от оцениваемого параметра σ, а зависит лишь от объема выборки п. Преобразуем неравенство (*) так, чтобы оно приняло вид χ1< χ< χ2. Вероятность этого неравенства (см. гл. XI, § 2) равна заданной вероятности γ, т.е.
Предполагая, что q < 1, перепишем неравенство (*) так:
Умножив все члены неравенства на
Вероятность того, что это неравенство, а следовательно, и равносильное ему неравенство (*) будет осуществлено, равна
Из этого уравнения можно по заданным п и γнайти q. Практически для отыскания q пользуются таблицей приложения 4. Вычислив по выборке s и найдя по таблице q, получим искомый доверительный интервал (*), покрывающий σ с заданной надежностью γ, т. е. интервал s (1 -q) <σ<s (1 +q). Пример 1. Количественный признак X генеральной совокупности распределен нормально. По выборке объема п = 25 найдено «исправленное» среднее квадратическое отклонение s = 0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,95.
Решение. По таблице приложения 4 по данным γ = 0,95 и n = 25 найдем q = 0, 32. Искомый доверительный интервал (*) таков: 0,8 (1—0,32) < σ < 0,8 (1+0,32), или 0,544 < σ < 1,056. Замечание. Выше предполагалось, что q < 1. Если q > 1, то неравенство (*) примет вид (учитывая, что σ> 0) 0 < σ< s (1 +q), или (после преобразований, аналогичных случаю q < 1)
Следовательно, значения q > 1 могут быть найдены из уравнения
Практически для отыскания значений q > 1, соответствующих различным заданным n и γ, пользуются таблицей приложения 4. Пример 2. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n =10 найдено «исправленное» среднее квадратическое отклонение s =0,16. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,999. Решение. По таблице приложения 4 по данным γ=0,999 и n =10 найдем q =1,80 (q> 1). Искомый доверительный интервал таков: 0 < σ < 0,16(1 + 1,80), или 0 < σ < 0,448.
Пояснение. Покажем, что плотность распределения χ имеет вид (**). Если случайная величина X распределена по закону χ2 с k = n- 1 степенями свободы, то ее плотность распределения (см. гл. XII, § 13)
или после подстановки k= n- 1
Воспользуемся формулой (см. гл. XII, § 10)
чтобы найти распределение функции
Так как χ > 0, то
Выполнив элементарные преобразования и изменив обозначения (g (χ),заменим на R (χ, n)), окончательно получим
Оценка точности измерений
В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения σ случайных ошибок измерений. Для оценки σ используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то теория, изложенная в предыдущем параграфе, применима для оценки точности измерений. Пример. По 15 равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s = 0,12. Найти точность измерений с надежностью 0,99. Решение. Точность измерений характеризуется средним квадратическим отклонением σ случайных ошибок, поэтому задача сводится к отысканию доверительного интервала (*), покрывающего σ с заданной надежностью 0,99 (см. § 18). По таблице приложения 4 по γ = 0,99 и n =15 найдем q = 0,73. Искомый доверительный интервал 0,12(1—0,73) < σ < 0,12(1+0,73), или 0,03 < σ < 0,21.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.238.6 (0.007 с.) |

 =42,319 и «исправленное» среднее квадратическое отклонение s=5,0. Требуется оценить истинное значение измеряемой величины с надежностью γ=0,95.
=42,319 и «исправленное» среднее квадратическое отклонение s=5,0. Требуется оценить истинное значение измеряемой величины с надежностью γ=0,95.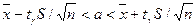 ,
, .
. = 42,319 - 3,85 = 38,469;
= 42,319 - 3,85 = 38,469;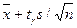 = 42,319+3,85 = 46,169.
= 42,319+3,85 = 46,169.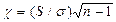
 . (**)
. (**) .
. .
. , получим
, получим , или
, или 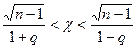 .
. .
.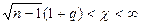

 ,
, .
. ,
,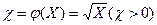 . Отсюда обратная функция
. Отсюда обратная функция и
и  .
. , следовательно,
, следовательно, .
. .
.


