
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отыскание параметров выборочного уравнения прямой линии среднеквадратичной регрессии по не сгруппированным даннымСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть изучается система количественных признаков (X, Y). В результате n независимых опытов получены и пар чисел (х1, у1), (х2, y2),..., (хn, yn). Найдем по данным наблюдений выборочное уравнение прямой линии среднеквадратичной регрессии (см. гл. XIV, § 20). Для определенности будем искать уравнение
регрессии Y на X. Поскольку различные значения x признака Х и соответствующие им значения у признака Y наблюдались по одному разу, то группировать данные нет необходимости. Также нет надобности использовать понятие условной средней, поэтому искомое уравнение можно записать так: У = kх + b. Угловой коэффициент прямой линии регрессии Y на Х называют выборочным коэффициентом регрессии Y на Х и обозначают через ρyx; он является оценкой коэффициента регрессии β (см. гл. XIV, § 20). Итак, будем искать выборочное уравнение прямой линии регрессии Y на Х вида Y = ρyxx + b. (*)
Подберем параметры ρyx и b так, чтобы точки (х1, у1), (х2, y2),..., (хn, yn), построенные по данным наблюдений, на плоскости хОу лежали как можно ближе к прямой (*). Уточним смысл этого требования. Назовем отклонением разность Yi - yi (i = 1, 2..... n), где Yi—вычисленная по уравнению (*) ордината, соответствующая наблюдаемому значению хi; уi—наблюдаемая ордината, соответствующая хi. Подберем параметры ρyx и b так, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция F этих параметров (временно вместо ρyx будем писать ρ):
или
Для отыскания минимума приравняем нулю соответствующие частные производные:
Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно ρ и b*):
Решив эту систему, найдем искомые параметры:
Аналогично можно найти выборочное уравнение прямой линии регрессии Х на Y:
где ρxy —выборочный коэффициент регрессии Х на Y. Пример. Найти выборочное уравнение прямой линии регрессии Y на Х по данным n = 5 наблюдений: х 1,00 1,50 3,00 4,50 5,00 у 1,25 1,40 1,50 1,75 2,25 Решение. Составим расчетную табл. 11. Найдем искомые параметры, для чего подставим вычисленные по таблице суммы в соотношения (***): ρxy = (5·26,975— 15·8,15)/(5·57,5—152) ==0,202; Ь= (57,5·8,15—15·26,975)/62,5= 1,024. (Для простоты записи вместо
Таблица 11
Напишем искомое уравнение регрессии:
Y = 0,202x + 1,024.
Для того чтобы получить представление, насколько хорошо вычисленные по этому уравнению значения Yi согласуются с наблюдаемыми значениями уi найдем отклонения Yi—уi. Результаты вычислений приведены в табл. 12.
Таблица 12
Как видно из таблицы, не все отклонения достаточно малы. Это объясняется малым числом наблюдений.
§ 5. Корреляционная таблица При большом числе наблюдений одно и то же значение х может встретиться nx раз, одно и то же значение у — ny раз, одна и та же пара чисел (х, у) может наблюдаться nxy раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты nx, ny, nxy. Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной. Поясним устройство корреляционной таблицы на примере табл. 13.
Таблица 13
В первой строке таблицы указаны наблюдаемые значения (10; 20; 30; 40) признака X, а в первом столбце— наблюдаемые значения (0,4; 0,6; 0,8) признака Y. На пересечении строк и столбцов находятся частоты nxy наблюдаемых пар значений признаков. Например, частота 5 указывает, что пара чисел (10; 0,4) наблюдалась 5 раз. Все частоты помещены в прямоугольнике, стороны которого проведены жирными отрезками. Черточка означает, что соответственная пара чисел, например (20; 0,4), не наблюдалась. В последнем столбце записаны суммы частот строк. Например, сумма частот первой строки «жирного» прямоугольника равна ny = 5+7+ 14 = 26; это число указывает, что значение признака Y, равное 0,4 (в сочетании с различными значениями признака X), наблюдалось 26 раз. В последней строке записаны суммы частот столбцов. Например, число 8 указывает, что значение признака X, равное 10 (в сочетании с различными значениями признака Y), наблюдалось 8 раз. В клетке, расположенной в нижнем правом углу таблицы, помещена сумма всех частот (общее число всех наблюдений n). Очевидно,
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 888; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.44.46 (0.008 с.) |

 =kx+b
=kx+b ,
, .
.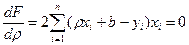 ;
; .
. ;
;  . (**)
. (**) ;
; . (***)
. (***) = ρxy x + C,
= ρxy x + C, условимся писать
условимся писать  .
.



 . В нашем примере
. В нашем примере = 8+21+13+18=60 и
= 8+21+13+18=60 и  = 26+12+22 = 60.
= 26+12+22 = 60.


