
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет теоретической линии регрессииСодержание книги Поиск на нашем сайте
Теоретическая линия регрессии представляет собой такую математически правильную кривую (либо прямую) линию, которая проходит наиболее близко к точкам эмпирической линии регрессии, выражает общую закономерность средних изменений признака в связи со средними изменениями фактора. В нашем случае характер размещения точек на корреляционном поле делает весьма вероятной гипотезу о линейной связи у от х: у = a0 + a1x. Параметры уравнения найдем из системы по способу наименьших квадратов: naꞌ0 + aꞌ1∑ xꞌ = ∑ yꞌ aꞌ0∑xꞌ + aꞌ1∑(xꞌ)2 = ∑ xꞌyꞌ Исходную информацию для решения данной системы получаем из таблицы 1.7., которая основана на результатах таблицы 1.6. Примем условный нуль в пятом интервале по оси Ох, тогдаС
Таблица 1.7.
В качестве проверки правильности данной таблицы должно соблюдаться равенство итогов четвертой строки и второго столбца. Если это условие не соблюдается, то в расчетах допущена ошибка, которая может привести к существенным искажениям величины параметров теоретической линии регрессии. В систему уравнений, данную выше, и получим: 11*a0’-12*a1’= -1 -12*a0’+148*a1’=-17 В качестве метода решения системы принимаем метод Гаусса, который позволяет находить решение последовательно, исключая неизвестные. Для этого первое уравнение умножаем на -12, а второе на 11 и вычтем: -1772*а1’=-199 a1’=0.11 Затем в первое уравнение системы подставим значение a1’ и находим величину a0’: 11*a0’-12*0.11= -1
a0’=0.03 Параметры a0’и a1’ необходимо преобразовать исходя из фактических значений х и у. Формулы перевода из упрощенных в реальные координаты: a1=a1’* где iy- интервал группировки по функции ix- интервал группировки по аргументу cy-новое начало отсчета по функции cx-новое начало отсчета по аргументу По этим формулам получаем, что a0=5290.54, a1= 17.79 Уравнение теоретической линии регрессии в реальных коэффициентах имеет вид y=5290.54+17.79х. В уравнении регрессии первое слагаемой носит название свободного члена, второе слагаемое называется коэффициентом регрессии. Он показывает, на сколько натуральных единиц изменяется в среднем результативный признак при изменении факторного признака на единицу. В нашем примере из уравнения теоретической линии регрессии видно, что выработка на 1 рабочего повышаются на 17.79 % при увеличении уровня сборности 1 %. Выработка на 1 рабочего, не зависящие от рассматриваемых фактов, равен 5290,54 тыс. руб. Для графического изображения линии регрессии, рассчитанной по линейной гипотезе, достаточно определить две точки, через которые можно провести прямую. В нашем примере по х1=60 и х2=70,у1=6357,94 и у2=6535,84 проводим на поле корреляции прямую линию. Вывод: Графическое изображение теоретической линии регрессии в виде уравнения прямой еще раз подтверждает наличие корреляционной связи между изучаемыми признаками.
Измерение тесноты связи Коэффициент корреляции ry/x является одним из наиболее совершенных методов измерения тесноты связи. Коэффициент корреляции отвечает на вопрос, в какой мере соблюдается строгая пропорциональность в изменениях функционального и факториального признаков. Коэффициент корреляции может принимать как положительные, так и отрицательные значения, т.е. -1≤r≤1. При выполнении корреляционных расчетов, когда связь между признаками х и у выражается прямой линией, соблюдается условие, при котором знак при коэффициенте корреляции ry/x должен совпадать со знаком при коэффициенте регрессии а1. Для расчета коэффициента корреляции существует формула, представленная в упрощенных координатах признаков х и у. ry/x= В нашем случае исходную информацию для нахождения ry/x принимаем из таблицы 1.7. ry/x= Вывод: выполненные расчеты показывают, что между выработкой на 1 рабочего и уровнем сборности существует положительная корреляция, которая говорит о том, что с увеличением факторного признака х функциональный признак у увеличивается. Знак при коэффициенте корреляции совпадает со знаком регрессии а1, что свидетельствует о правильности произведенных вычислений. Имеем слабую связь между изучаемыми явлениями.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.143 (0.009 с.) |

 =61,9%; i = 1,46 %.
=61,9%; i = 1,46 %. y x
y x
 a0=cy+iya0’-a1’*
a0=cy+iya0’-a1’* 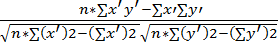
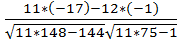 = 0,16
= 0,16


