
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение рядов распределения по факторному и результативному признакамСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
a) интервальный ряд распределения: Для корреляционного анализа зависимости результативного признака у от факторного признака х необходима статистическая обработка данных. Первоначально систематизация статистического материала производится по величине изучаемого признака в порядке убывания или возрастания, то есть необходимо произвести ранжирование рядов распределения. При построении интервального ряда распределения определяем величину интервала i, которую вычисляем по формуле: i = где Rmax-максимальное значение переменной; Rmin-минимальное значение переменной; n- число интервалов. Ориентировочно число интервалов определяется по формуле n= 1+3,32lgN В нашем случае получаем n=10. Итак, подставим значения из таблицы 1.1. в формулу (1) и получим длину интервала по выработке на 1 рабочего в год по объему работ собственными силами: iy = ix = Начальная граница первого интервального ряда равна Для выработки на 1 рабочего: 1/2*224,8=112,4, тогда Нижняя граница 1 интервала: 5234-112,4=5121,6 т. руб. Верхняя граница 1 интервала: 5121,6+224,8=5346, 4 т. руб. Для объема работ собственными силами: 1/2*1,46=0,73, тогда Нижняя граница 1 интервала: 54,6-0,73=53,87% Верхняя граница 1 интервала: 53,87+1,46=55,33 % Интервальные ряды по функциональному признаку (по выработке на 1 рабочего) и по факторному признаку (объем работ собственными силами): Таблица 1.2.
б) дискретные ряды распределения: С помощью таблицы 1.2. построим дискретные ряды распределения по y и x. Для выполнения корреляционных расчетов интервальные ряды распределения необходимо представить в дискретной форме. В связи с этим вместо размерности интервалов принимаем их центральные значения, которые рассчитываются как средние арифметические величины начала и конца интервалов. Результаты расчетов приведем в табличной форме: Дискретный ряд распределения по у (по выработке на 1 рабочего) Таблица 1.3.
Плотность распределения определяется по формуле: ρ= Таким образом, ряд распределения по выработке на 1 рабочего показывает, что наиболее характерным является группа с центральным значением интервала 6133,2, 6582,8, 6807,6 тыс. руб., так как они составляют 18,18 % от всего количества выработки на 1 рабочего. Дискретный ряд распределения по х (по уровню сборности) Таблица 1.4.
Таким образом, ряд распределения по уровню сборности показывает, что наиболее характерным является группа центральным значением интервала 57,52%, так как она составляет по 27,27 %. Построение корреляционной таблицы Для построения корреляционной таблицы на поле корреляции накладывается сетка, соответствующая интервальным рядам распределения по факторному и функциональному признакам. Затем подсчитывается число точек (частот) в каждой клетке координатной сетки. Таблица 1.5
Результаты расчетов, выполненные в таблице 1.5, позволяют сделать вывод о том, что при переходе слева направо в сторону больших значений факторного признака х соответствующие ряды распределения функционального признака у смещаются сверху вниз, т.е. в сторону меньших значений функций. Следовательно, выработка на 1 рабочего в год находится в корреляционной зависимости от уровня сборности.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.60.29 (0.008 с.) |

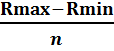
 =
= 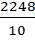 = 224,8 т. руб.
= 224,8 т. руб.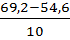 =
= 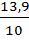 =1,46 %
=1,46 % i.
i.



