
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение показателей вариацииСодержание книги Поиск на нашем сайте
Корреляционный анализ 1.1. Построение рядов распределения по факторному и результативному признакам: А) дискретный ряд распределения; Б) интервальный ряд распределения; 1.2. Построение поля корреляции; 1.3. Построение корреляционной таблицы; 1.4. Расчет и построение эмпирической линии регрессии; 1.5. Расчет и построение теоретической линии регрессии; 1.6. Измерение тесноты связи; 1.7. Проверка правильности гипотезы о прямолинейной форме корреляционной связи; 1.8. Анализ выполненных расчетов и вывод. 1.9. Общий вывод по разделу «Корреляционный анализ» Определение показателей вариации 2.1. Вычисление групповой дисперсии; 2.2. Вычисление средней из групповых; 2.3. Вычисление межгрупповой дисперсии 2.4. Вычисление общей дисперсии 2.5. Вычисление среднеквадратического отклонения 2.6. Вычисление показателей вариации; 2.7. Вычисление эмпирического коэффициента детерминации; 2.8. Вычисление эмпирического корреляционного отношения. 2.9. Общий вывод по разделу «Определение показателей вариации». Анализ динамических рядов. 3.1. Определение данных для 3-ого динамического ряда по двум исходным данным; 3.2. Установление вида ряда динамики; 3.3. Определение среднего уровня динамики; 3.4. Определение показателей изменения уровня ряда динамики: базисные и цепные абсолютные приросты, темпы роста и прироста, абсолютное значение прироста; 3.5. Вычисление средний абсолютный прирост; 3.6. Вычисление среднегодовых темпов роста и прироста; 3.7. Графическое изображение (линейный график) показателей динамических рядов: базисные и цепные темпы роста по трем динамическим рядам; 3.8. Выявление основной тенденции развития одного из динамических рядов методом скользящей средней (трехчленной); 3.9. Провести аналитическое выравнивание динамического ряда 3.10. Анализ полученных показателей динамических рядов. 3.11. Графическое изображение скользящей прямой, прямой по исходным данным, выровненной прямой. 3.12. Общий вывод по разделу «Анализ динамических рядов»
Корреляционный анализ Вариант I. Таблица 1.1.
Построение рядов распределения по факторному и результативному признакам a) интервальный ряд распределения: Для корреляционного анализа зависимости результативного признака у от факторного признака х необходима статистическая обработка данных. Первоначально систематизация статистического материала производится по величине изучаемого признака в порядке убывания или возрастания, то есть необходимо произвести ранжирование рядов распределения. При построении интервального ряда распределения определяем величину интервала i, которую вычисляем по формуле: i = где Rmax-максимальное значение переменной; Rmin-минимальное значение переменной; n- число интервалов. Ориентировочно число интервалов определяется по формуле n= 1+3,32lgN В нашем случае получаем n=10. Итак, подставим значения из таблицы 1.1. в формулу (1) и получим длину интервала по выработке на 1 рабочего в год по объему работ собственными силами: iy = ix = Начальная граница первого интервального ряда равна Для выработки на 1 рабочего: 1/2*224,8=112,4, тогда Нижняя граница 1 интервала: 5234-112,4=5121,6 т. руб. Верхняя граница 1 интервала: 5121,6+224,8=5346, 4 т. руб. Для объема работ собственными силами: 1/2*1,46=0,73, тогда Нижняя граница 1 интервала: 54,6-0,73=53,87% Верхняя граница 1 интервала: 53,87+1,46=55,33 % Интервальные ряды по функциональному признаку (по выработке на 1 рабочего) и по факторному признаку (объем работ собственными силами): Таблица 1.2.
б) дискретные ряды распределения: С помощью таблицы 1.2. построим дискретные ряды распределения по y и x. Для выполнения корреляционных расчетов интервальные ряды распределения необходимо представить в дискретной форме. В связи с этим вместо размерности интервалов принимаем их центральные значения, которые рассчитываются как средние арифметические величины начала и конца интервалов. Результаты расчетов приведем в табличной форме: Измерение тесноты связи Коэффициент корреляции ry/x является одним из наиболее совершенных методов измерения тесноты связи. Коэффициент корреляции отвечает на вопрос, в какой мере соблюдается строгая пропорциональность в изменениях функционального и факториального признаков. Коэффициент корреляции может принимать как положительные, так и отрицательные значения, т.е. -1≤r≤1. При выполнении корреляционных расчетов, когда связь между признаками х и у выражается прямой линией, соблюдается условие, при котором знак при коэффициенте корреляции ry/x должен совпадать со знаком при коэффициенте регрессии а1. Для расчета коэффициента корреляции существует формула, представленная в упрощенных координатах признаков х и у. ry/x= В нашем случае исходную информацию для нахождения ry/x принимаем из таблицы 1.7. ry/x= Вывод: выполненные расчеты показывают, что между выработкой на 1 рабочего и уровнем сборности существует положительная корреляция, которая говорит о том, что с увеличением факторного признака х функциональный признак у увеличивается. Знак при коэффициенте корреляции совпадает со знаком регрессии а1, что свидетельствует о правильности произведенных вычислений. Имеем слабую связь между изучаемыми явлениями.
Вычисление общей дисперсии Зная среднюю из групповых дисперсий и межгрупповую, дисперсию, можно определить по правилу сложения общую дисперсию исследуемой совокупности. Общая дисперсия тоже не имеет единицы измерения. Она вычисляется по формуле: σ2=σi2+δ2=75031+243024= 318055 тыс. руб. Сделаем проверку правильности вычислений. Для этого сделаем соответствующие вычисления по формуле общей дисперсии: σi2= σi2= В нашем случае используем формулу для не сгруппированных данных, где: yi - значения признака ȳi -общее среднее значение признака по всем группам n - количество значений σ2= Т.о. мы получили, что значения совпали, т.е. все проделанные выше вычисления верны. Вывод: в дальнейшем при помощи общей дисперсии мы сможем вычислить эмпирический коэффициент детерминации, который поможет определить долю межгрупповой дисперсии в общей.
Заключение по разделу «Определение показателей вариации» В первом пункте данного раздела мы вычислили групповую дисперсию для каждой полученной группы и сделали соответствующий вывод: групповые дисперсии, вычисленные по трем группам, отражают действие всех факторов влияющих на величину накладных расходов. Затем вычисляем среднюю из групповых дисперсий. Данная величина показала зависимость всех рядов совокупности от неучтенных факторов, которые могут воздействовать на эту совокупность. Следующими действиями были вычисление межгрупповой дисперсии. Мы увидели, что чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние факторного признака на результативный признак, т.е. на выработку на 1 рабочего. Затем вычислили общую дисперсию правилом сложения и проверили наши получившиеся значения. Вычисленное далее эмпирический коэффициент детерминации показал, что связь между факторным и результативным признаком весьма тесная. Среднее квадратическое отклонение выявило, что накладные расходы отклоняется от средней величины на 564 тыс. руб. В пункте вычисления показателя вариации мы получили, что измеряемая совокупность является однородной, т.к. коэффициент вариации не превышает 33 %. Здесь это условие выполняется, значит, средняя величина характерна для данной совокупности. С помощью вычисленных общей и межгрупповой дисперсии мы вычислили коэффициент детерминации, который показал, что величина выработки на 1 рабочего на 76% зависит от уровня сборности и на 24 % зависит от всех остальных факторов. И в заключении, вычислили эмпирическое корреляционное отношение, указывающее на тесную связь выработкой на 1 рабочего и уровнем сборности.
АНАЛИЗ ДИНАМИЧЕСКИХ РЯДОВ. Исходные данные для выполнения данной задачи: Вариант №6
Заключение по разделу «Анализ динамических рядов» В самом начале раздела мы определили название третьего ряда. Для этого мы значения стоимости активной части ОПФ поделили на среднесписочную численность работников и получили механовооруженность. Далее мы определили, что у нас моментный ряд динамики. Затем нашли значения среднего уровня моментного ряда с равноотстоящими датами, по соответствующей формуле. В третьем пункте рассмотрели по отдельности показания изменения уровня динамики, такие как базисный и цепной абсолютные приросты, темпы роста и прироста, абсолютные значения прироста. Для каждого динамического ряда составили соответствующие таблицы. По таблице 3.3. можно сделать вывод, что: 1. с каждым годом абсолютные базисные темпы прироста увеличивались; 2. в цепных абсолютных темпах роста наблюдается неровное уменьшение, в 1994 году наблюдается спад, но в 1995 начинает увеличиваться и в 1996 достигает 4%. Но в 1998 наблюдается спад до -3%; 3. базисные темпы роста тоже с каждым годом увеличивались, лишь в 1998 году понижается на 2.7%. А в тенденции цепного темпа роста наблюдаются скачки такого же рода, что в абсолютных приростах; 4. базисные и цепные темпы прироста аналогичны случаю базисному и цепному темпу роста; 5. абсолютное значение 1% прироста в периоде с 1991 до 1998 года только увеличивается.
По таблице 3.4. можно сделать вывод, что: 1. базисный абсолютный прирост стабильно возрастает, в отличие от цепного, где происходит резкое понижение с 1997 года; 2. в базисном темпе роста наблюдается стабильное увеличение, а в цепном развитие скачкообразное(понижение и увеличение) только с 1996 года наблюдается стабильный спад; 3. в базисном и цепном темпах прироста наблюдается аналогичность ситуации базисного и цепного темпа роста; 4. абсолютное значение 1% прироста в периоде с 1991 до 1998 только увеличивается. По таблице 3.5. можно сделать вывод, что: 1. в базисном абсолютном приросте наблюдается стабильный подъем, а в цепном наблюдается уменьшение до 1995 года, а с1996 стабильный рост; 2. базисный темп роста стабильно уменьшается, а в цепном идет чередование роста и спада; 3. тенденция, прослеживаемая в базисном и цепном темпах прироста аналогична темпу их роста; 4. абсолютное значение 1% прироста в периоде с 1991 до 1998 только увеличивается. По вычислениям среднего абсолютного прироста можно сделать вывод, что каждый ряд имеет положительный прирост. Если рассматривать связь между данными абсолютного прироста, то можно сказать, что из-за того, что объем СМР и среднегодовая стоимость ОПФ имеют положительный абсолютный прирост, у фондоотдачи он тоже положителен. Фондоотдача напрямую зависит от первых двух показателей, так как исходные данные третьего ряда основаны на исходных данных первых двух рядов. Далее мы вычисляем средние темпы роста и прироста, который приводят нас к следующим выводам: 1. Среднегодовые темпы роста для объема СМР составляют 134%, т.е. в каждом последующем году, по сравнению с предыдущим годом происходит увеличение объема СМР на 34%. 2. Среднегодовые темпы роста для среднегодовой стоимости ОПФ составляют 103%, т.е. в каждом последующем году, по сравнению с предыдущим годом происходит увеличение среднегодовой стоимости на 3%. 3. Среднегодовые темпы роста для фондоотдачи составляют 102%, т.е. в каждом последующем году, по сравнению с предыдущим годом происходит увеличение среднегодовой стоимости на 2%.
Список литературы: 1. Гусаров В.М. Теория статистики. М. «Аудит», Издательское объединение «ЮНИТИ»,1998. 2. Спирин А.А., Башина О.Э. Общая теория статистики, М.: «Финансы и статистика», 1994. 3. Полисюк Г.Б. Экономико-математические методы планирования строительства М.: «Стройиздат», 1986 г. 4. Харисова Г.М. Методические указания к выполнении. Курсовой работы по курсу «Статистика» для студентов специальности 060800, 29150. Казань: КГАСА, 2004.-23с.
Корреляционный анализ 1.1. Построение рядов распределения по факторному и результативному признакам: А) дискретный ряд распределения; Б) интервальный ряд распределения; 1.2. Построение поля корреляции; 1.3. Построение корреляционной таблицы; 1.4. Расчет и построение эмпирической линии регрессии; 1.5. Расчет и построение теоретической линии регрессии; 1.6. Измерение тесноты связи; 1.7. Проверка правильности гипотезы о прямолинейной форме корреляционной связи; 1.8. Анализ выполненных расчетов и вывод. 1.9. Общий вывод по разделу «Корреляционный анализ» Определение показателей вариации 2.1. Вычисление групповой дисперсии; 2.2. Вычисление средней из групповых; 2.3. Вычисление межгрупповой дисперсии 2.4. Вычисление общей дисперсии 2.5. Вычисление среднеквадратического отклонения 2.6. Вычисление показателей вариации; 2.7. Вычисление эмпирического коэффициента детерминации; 2.8. Вычисление эмпирического корреляционного отношения. 2.9. Общий вывод по разделу «Определение показателей вариации». Анализ динамических рядов. 3.1. Определение данных для 3-ого динамического ряда по двум исходным данным; 3.2. Установление вида ряда динамики; 3.3. Определение среднего уровня динамики; 3.4. Определение показателей изменения уровня ряда динамики: базисные и цепные абсолютные приросты, темпы роста и прироста, абсолютное значение прироста; 3.5. Вычисление средний абсолютный прирост; 3.6. Вычисление среднегодовых темпов роста и прироста; 3.7. Графическое изображение (линейный график) показателей динамических рядов: базисные и цепные темпы роста по трем динамическим рядам; 3.8. Выявление основной тенденции развития одного из динамических рядов методом скользящей средней (трехчленной); 3.9. Провести аналитическое выравнивание динамического ряда 3.10. Анализ полученных показателей динамических рядов. 3.11. Графическое изображение скользящей прямой, прямой по исходным данным, выровненной прямой. 3.12. Общий вывод по разделу «Анализ динамических рядов»
Корреляционный анализ Вариант I. Таблица 1.1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.214.16 (0.007 с.) |

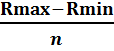
 =
= 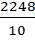 = 224,8 т. руб.
= 224,8 т. руб.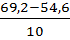 =
= 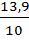 =1,46 %
=1,46 % i.
i.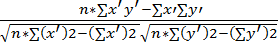
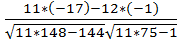 = 0,16
= 0,16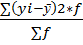 - для сгруппированных данных
- для сгруппированных данных - для несгруппированных данных
- для несгруппированных данных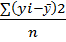 =
= 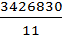 = 318055 тыс. руб.
= 318055 тыс. руб.


