
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий вывод по разделу «корреляционный анализ»Содержание книги Поиск на нашем сайте
По данным таблицы 1.1 мы построили интервальные и дискретные ряды. При помощи таблицы 1.2. сделали вывод, что ряд распределения по выработке на 1 рабочего показывает, что наиболее характерным является группа с центральным значением интервала 6133,2, 6582,8, 6807,6 тыс. руб., так как они составляют 18,18 % от всего количества выработки на 1 рабочего. Ряд распределения по уровню сборности показывает, что наиболее характерным является группа с центральным значением интервала 61,9, так как составляет 27,27%. Затем мы строим корреляционную таблицу, которая показывает, что при переходе слева направо в сторону больших значений факторного признака х соответствующие ряды распределения функционального признака у смещаются сверху вниз, т.е. в сторону меньших значений функций. Следовательно, выработка на 1 рабочего в год находится в корреляционной зависимости от уровня сборности Далее считаем эмпирическую линию регрессии. После всех расчетов можно было сделать вывод о том, что расчет эмпирической линии регрессии вновь подтвердил наличие корреляционной зависимости между выработкой на 1 рабочего и уровнем сборности. При расчете теоретической линии регрессии из уравнения теоретической линии регрессии видно, что выработка на 1 рабочего увеличивается на 17,79% при увеличении численности на 1 %. Уровень сборности, не зависящая от рассматриваемых факторов равна 5290,54 Затем просчитываем коэффициент корреляции, который помогает определить тесноту связи между результативным и факторным признаком и сделали вывод, что выполненные расчеты показывают, что между выработкой на 1 рабочего в год и объемом работ собственными силами существует положительная корреляция, которая говорит о том, что с увеличением факторного признака х функциональный признак у увеличивается. Знак при коэффициенте корреляции совпадает со знаком регрессии а1, что свидетельствует о правильности произведенных вычислений. Случайные факторы оказывают большое влияние на функцию, т.к. r=0,16, следовательно, имеем слабую связь между изучаемыми явлениями. В заключении, мы выяснили при помощи расчета коэффициента детерминации, что имеется кое какое отклонение, однако оно не существенно и доказали это утверждение нахождением показателя t.
Определение показателей вариации Вариация- это различия в значении какого-либо признака у разных единиц изучаемой совокупности в один и тот же момент времени. Из исходных данных, которые мы взяли из первого раздела (корреляционный анализ) выделить три группы по результативному признаку у: Исходные данные: Таблица 2.1.
Таблица 2.2.
Для каждой группы просчитаем ȳi= В статистике очень часто используется показатель, который называется дисперсия, представляющая собой среднеквадратическое отклонение индивидуальных значений признака от средней величины. Дисперсия – неименованная величина, т.е. она не имеет единиц измерения. Она рассчитывается как для сгруппированных данных, когда имеет частота признака f, так и для не сгруппированных данных.
Вычисление групповой дисперсии Групповая дисперсия отражает случайную вариацию, обусловленную влиянием неучтенных факторов и независящую от признака фактора положенного в основание группировки. Она рассчитывается как для сгруппированных, когда имеет частоту признака, так и для не сгруппированных данных. Для сгруппированных данных: σi2= σi2= где: yi – значение признака; ȳi – среднее значение в выборке; n - число наблюдений в выборке; f – частоты признака В данном случае вычисляем групповую дисперсию по формуле для не сгруппированных данных, т.к. у нас не имеется частоты признака f. Подставив данные в таблице 2.2., найдем дисперсию каждой из трех групп: σ12 = σ22 = σ32 = Вывод: групповые дисперсии, вычисленные по трем группам, отражают действие всех факторов влияющих на величину выработки на 1 рабочего.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.238.6 (0.006 с.) |

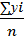 . По данной формуле определим средние значения результативного признака для каждой из данных групп и запишем их в таблицу.
. По данной формуле определим средние значения результативного признака для каждой из данных групп и запишем их в таблицу.

 =95393
=95393


