
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное разыгрывание нормальной случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Напомним предварительно, что если случайная величина R распределена равномерно в интервале (0,1), то ее математическое ожидание и дисперсия соответственно равны (см. гл. XII, § 1, замечание 3): M (R) = 1/2, (*) D (R) = 1/2. (**) Составим сумму п независимых, распределенных равномерно в интервале (0,1) случайных величин Rj (j =1, 2,...,n):
Для нормирования этой суммы найдем предварительно ее математическое ожидание и дисперсию. Известно, что математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Сумма (***) содержит п слагаемых, математическое ожидание каждого из которых в силу (*) равно 1/2; следовательно, математическое ожидание суммы (***)
Известно, что дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых. Сумма (***) содержит n независимых слагаемых, дисперсия каждого из которых в силу (**) равна 1/12; следовательно, дисперсия суммы (***)
Отсюда среднее квадратическое отклонение суммы (***)
Пронормируем рассматриваемую сумму, для чего вычтем математическое ожидание и разделим результат на среднее квадратическое отклонение:
В силу центральной предельной теоремы при п→∞ распределение этой нормированной случайной величины стремится к нормальному с параметрами а= 0 и σ=1. При конечном п распределение приближенно нормальное. В частности, при п = 12 получим достаточно хорошее и удобное для расчета приближение
Правило. Для того чтобы разыграть возможное значение xi нормальной случайной величины Х с параметрами а=0 и σ=1, надо сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:
Пример, а) Разыграть 100 возможных значений нормальной величины Х с параметрами а=0 и σ=1; б) оценить параметры разыгранной величины. Решение. а) Выберем 12 случайных чисел из первой строки таблицы *), сложимих и из полученной суммы вычтем 6; в итоге имеем xi =(0,10+0,09+...+0,67) - 6= - 0,99. Аналогично, выбирая из каждой следующей строки таблицы первые 12 чисел, найдем остальные возможные значения X. б) Выполнив расчеты, получим искомые оценки:
Оценки удовлетворительные: а* близко к нулю, σ* мало отличается от единицы. Замечание. Если требуется разыграть возможное значение zi, нормальной случайной величины Z с математическим ожиданием а и средним квадратическим отклонением σ, то, разыграв по правилу настоящего параграфа возможное значение xi, находят искомое возможное значение по формуле
zi=σxi+a. Эта формула получена из соотношения (zi-a) /σ=xi. Задачи 1. Разыграть 6 значений дискретной случайной величины X, закон распределения которой задан в виде таблицы
Указание. Для определенности принять, что выбраны случайные числа: 0,73; 0,75; 0,54; 0,08; 0,28; 0,53. Отв. 10; 10; 10; 2; 3; 22; 10. 2. Разыграть 4 испытания, в каждом из которых вероятность появления события А равна 0,52. Указание. Для определенности принять, что выбраны случайные числа: 0;28; 0,53; 0,91; 0,89. Отв. А, 3. Заданы вероятности трех событий, образующих полную группу: Р (А 1)=0,20, Р (А 2)=0,32, Р (А3) = 0,48. Разыграть 6 испытаний, в каждом из которых появляется одно из заданных событий. Указание. Для определенности принять, что выбраны случайные числа: 0,77; 0,19; 0,21; 0,51; 0,99; 0,33. Отв. А3, А 1, А 2, А 2, А3, А 2. 4. События А и В независимы и совместны. Разыграть 5 испытаний, в каждом из которых вероятность появления события А равна 0,5, а события В— 0,8. Указание. Составить полную группу событий: А 1= АВ, Отв. А 1, А 2, А 2, А 1, А3. 5. События А, В, С независимы и совместны. Разыграть 4 испытания в каждом из которых вероятности появления событий заданы: Р (А) = 0,4, Р (В) = 0,6, Р (С) = 0,5. Указание. Составить полную группу событий: Отв.А 1, А8, А4, А4. 6. События А и В зависимы и совместны. Разыграть 4 испытания, в каждом из которых заданы вероятности: Р (А)=0,7, Р (В)=0,6, Р (АВ)=0,4. Указание. Составить полную группу событий: А 1= АВ, Отв. А 1, А 2, А4, А3. 7. Разыграть 3 возможных значения непрерывной случайной величины X, которая распределена по показательному закону и задана функцией распределения F (х) = 1 - е-10x. Указание. Для определенности принять, что выбраны случайные числа: 0,67; 0,79; 0,91. Отв. 0,04; 0,02; 0,009. 8. Разыграть 4 возможных значения непрерывной случайной величины X, распределенной равномерно в интервале (6,14). Указание. Для определенности принять, что выбраны случайные числа: 0,11: 0,04; 0,61; 0,93.
Отв. 6,88; 6,32; 10,88; 13,44. 9. Найти методом суперпозиции явные формулы для разыгрывания непрерывной случайной величины X, заданной функцией распределения F (x)=1- (1/3)(2е-2x+е-3x:), 0< х <∞. Отв. х= - (1/2) 1п r 2, если r 1 < 2/3; х = - (1/3) 1п r 2, если r 1≥2/3. 10. Найти явную формулу для разыгрывания непрерывной случайной величины X, заданной плотностью вероятности f (х)= b /(1 + ax)2 в интервале 0≤ x ≤1/(b-a); вне этого интервала f(x)=0. Отв. хi = - ri /(b - ari). 11. Разыграть 2 возможных значения нормальной случайной величины с параметрами: а) а =0, σ =1; б) а =2, σ =3. Указание. Для определенности принять случайные числа (далее указано число сотых долей; например, числу 74 соответствует случайное число r 1=0,74): 74. 10, 88, 82. 22, 88, 57, 07, 40, 15, 25, 70; 62, 88, 08, 78, 73, 95, 16, 05, 92, 21, 22, 30. Отв. а) x 1= - 0,22, x 2= - 0.10; 6) z 1=1,34, z 2=2,70. Глава двадцать вторая
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.122 (0.011 с.) |

 (***)
(***)










 для определенности принять случайные числа: 0,34; 0,41; 0,48; 0,21; 0,57.
для определенности принять случайные числа: 0,34; 0,41; 0,48; 0,21; 0,57.
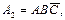





 для определенности принять, что выбраны случайные числа: 0,075; 0,907; 0,401; 0,344.
для определенности принять, что выбраны случайные числа: 0,075; 0,907; 0,401; 0,344.


