
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Начальные и центральные теоретические моментыСодержание книги
Поиск на нашем сайте
Рассмотрим дискретную случайную величину X, заданную законом распределения:
Найдем математическое ожидание X: М (Х) = 1 * 0, 6 + 2 * 0, 2 + 5 * 0, 19 + 100 * 0, 01 = 2, 95. Напишем закон распределения X 2:
Найдем математическое ожидание Х 2: М (Х 2) = 1 * 0, 6 + 4 * 0, 2 + 25 * 0, 19 + 10000 * 0, 01 = 106, 15. Видим, что М (X 2) значительно больше М (X). Это объясняется тем, что после возведения в квадрат возможное значение величины X 2, соответствующее значению x =100 величины X, стало равным 10 000, т. е. значительно увеличилось; вероятность же этого значения мала (0,01). Таким образом, переход от М (X)к М (X 2)позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина X имела несколько больших и маловероятных значений, то переход к величине X 2, а тем более к величинам X 3, X 4 и т. д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной). Начальным моментом порядка k случайной величины X называют математическое ожидание величины Xk: vk = M (X). В частности, v 1 = M (X), v 2 = M (X 2). Пользуясь этими моментами, формулу для вычисления дисперсии D (X) = M (X 2)— [ М (X)]2 можно записать так: D (X) = v 2 – Кроме моментов случайной величины X целесообразно рассматривать моменты отклонения X—М (X). Центральным моментом порядка k случайной величины X называют математическое ожидание величины (Х-М (Х)) k:
В частности,
Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая (*) и (***), получим m2= v 2 – Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы: m3= v 3 – 3 v 2 v 1 + 2 m4= v 4 – 4 v 3 v 1 + 6 v 2 Моменты более высоких порядков применяются редко. Замечание. Моменты, рассмотренные здесь, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими. Определения эмпирических моментов даны далее (см. гл. XVII, § 2).
Задачи
1. Известны дисперсии двух независимых случайных величин: D (X) = 4, D (Y)=3. Найти дисперсию суммы этих величин. Отв. 7. 2. Дисперсия случайной величины X равна 5. Найти дисперсию следующих величин: а) X —1; б) —2 Х; в) ЗХ + 6. Отв. а) 5; б) 20; в) 45. 3. Случайная величина X принимает только два значения: +С и —С, каждое с вероятностью 0,5. Найти дисперсию этой величины. Отв. С 2. 4. Найти дисперсию случайной величины, зная закон ее распределения
Отв. 67,6404. 5. Случайная величина X может принимать два возможных значения: х 1с вероятностью 0,3 и x 2 с вероятностью 0,7, причем х 2 > х 1. Найти x 1и x 2, зная, что М (Х) = 2, 7и D (X) =0,21. Отв. x 1 = 2, x 2 = 3. 6. Найти дисперсию случайной величины X —числа появлений событий А в двух независимых испытаниях, если М (Х) = 0, 8. Указание. Написать биномиальный закон распределения вероятностей числа появлений события А в двух независимых испытаниях. Отв. 0, 48. 7. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов таковы: р 1 = 0,3; р 2 = 0,4; p 3 = 0,5; р 4 = 0,6. Найти математическое ожидание и дисперсию числа отказавших приборов. Отв. 1,8; 0,94. 8. Найти дисперсию случайной величины X — числа появлений события в 100 независимых испытаниях, в каждом из которых вероятность наступления события равна 0,7. Отв. 21. 9. Дисперсия случайной величины D (Х) = 6,25. Найти среднее квадратическое отклонение s(X). Отв. 2, 5. 10. Случайная величина задана законом распределения
Найти среднее квадратическое отклонение этой величины. Отв. 2, 2. 11. Дсперсия каждой из 9 одинаково распределенных взаимно независимых случайных величин равна 36. Найти дисперсию среднего арифметического этих величин. Отв. 4. 12. Среднее квадратическое отклонение каждой из 16 одинаково распределенных взаимно независимых случайных величин равно 10. Найти среднее квадратическое отклонение среднего арифметического этих величин. Отв. 2,5.
Глава девятая ЗАКОН БОЛЬШИХ ЧИСЕЛ
Предварительные замечания
Как уже известно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.
Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли (имеются и другие теоремы, которые здесь не рассматриваются). Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли—простейшим. Для доказательства этих теорем мы воспользуемся неравенством Чебышева.
Неравенство Чебышева Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин. Для простоты ограничимся доказательством этого неравенства для дискретных величин. Рассмотрим дискретную случайную величину X, заданную таблицей распределения:
Поставим перед собой задачу оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа e. Если e достаточно мало, то мы оценим, таким образом, вероятность того, что X примет значения, достаточно близкие к своему математическому ожиданию. П. Л. Чебышев доказал неравенство, позволяющее дать интересующую нас оценку. Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше, чем 1 —D (Х) / e 2: Р (|Х —М (Х) |< e) Доказательство. Так как события, состоящие в осуществлении неравенств |Х—М (Х) |<e и |Х—М (Х) | Р (|Х —М (Х) |< e) + Р (|Х —М (Х) | Отсюда интересующая нас вероятность Р (|Х —М (Х) |< e) = 1- Р (|Х —М (Х) | Таким образом, задача сводится к вычислению вероятности Р (| Х—М (Х) | Напишем выражение дисперсии случайной величины X: D (X) = [ x 1 -M (X)]2 p 1 + [ x 2 -M (X)]2 p 2 +…+ [ xn -M (X)]2 pn. Очевидно, все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у которых | xi — M (Х)|< e (для оставшихся слагаемых | xj — M (Х)| D (X) Заметим, что обе части неравенства | xj — М (Х)| D (X) По теореме сложения, сумма вероятностей рк+ 1 + pk+ 2 + … + рn есть вероятность того, что X примет одно, безразлично какое, из значений xk+ 1, хк+ 2,.... хп, а при любом из них отклонение удовлетворяет неравенству | xj — М (Х)|
P (| X — М (Х)| Это соображение позволяет переписать неравенство (**) так: D (X) или P (| X — М (Х)| Подставляя (***) в (*), окончательно получим P (| X — М (Х)| < e) что и требовалось доказать. Замечание. Неравенство Чебышева имеет для практики ограниченное значение поскольку часто дает грубую, а иногда и тривиальную (не представляющую интереса) оценку. Например, если D (X) > e 2 и, следовательно, D (X) / e 2 > 1, то 1 — D (Х) / e 2 < 0; таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения неотрицательна, а это и без того очевидно, так как любая вероятность выражается неотрицательным числом. Теоретическое же значение неравенства Чебышева весьма велико. Ниже мы воспользуемся этим неравенством для вывода теоремы Чебышева.
Теорема Чебышева Теорема Чебышева. Если Х 1, Х 2 ,…, Хn,... — попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число е, вероятность неравенства
будет как угодно близка к единице, если число случайных величин достаточно велико. Другими словами, в условиях теоремы
Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым. Доказательство. Введем в рассмотрение новую случайную величину — среднее арифметическое случайных величин
Найдем математическое ожидание M Применяя к величине
или, учитывая соотношение (*),
Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим
По условию дисперсии всех случайных величин ограничены постоянным числом С, т. е. имеют место неравенства: D (X 1)
(D (X 1) + D (X 2) +…+D (Xn)) /n 2 Итак,
Подставляя правую часть (***) в неравенство (**) (отчего последнее может быть лишь усилено), имеем
Отсюда, переходя к пределу при
Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать
Теорема доказана. Выше, формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева. Обозначим математическое ожидание каждой из случайных величин через а; в рассматриваемом случае среднее арифметическое математических ожиданий, как легко видеть, также равно а. Мы можем сформулировать теорему Чебышева для рассматриваемого частного случая. Если Х 1, Х 2,..., Хп,... — попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число e > О, вероятность неравенства
будет как угодно близка к единице, если число случайных величин достаточно велико. Другими словами, в условиях теоремы будет иметь место равенство
Сущность теоремы Чебышева
Сущность доказанной теоремы такова: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу (М (X 1)+ М (Х 2) +...+М (Хп)) /п (или к числу а в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало. Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое. Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются. Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин; она является ярким примером, подтверждающим справедливость учения диалектического материализма о связи между случайностью и необходимостью.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1088; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.224.236 (0.014 с.) |

 . (*)
. (*)
 (**)
(**) (***)
(***) ,
, + 3
+ 3  .
. 1 —D (X) / e 2.
1 —D (X) / e 2. D (X) / e 2 (***)
D (X) / e 2 (***)
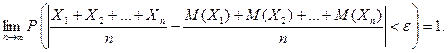
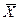 =(X 1 +X 2 +…+Xn) /n.
=(X 1 +X 2 +…+Xn) /n.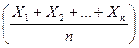 =
=  . (*)
. (*)
 (**)
(**) .
. . (***)
. (***)
 , получим
, получим






