
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции. Корреляционным моментом μху случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: μху={M[X-M (X) ][Y-M (Y) ]}, Для вычисления корреляционного момента дискретных величин используют формулу
а для непрерывных величин - формулу
Корреляционный момент служит для характеристики связи между величинами X и Y. Как будет показано ниже, корреляционный момент равен нулю, если X и Y независимы; следовательно, если корреляционный момент не равен нулю, то X и Y - зависимые случайные величины. Замечание 1. Учитывая, что отклонения есть центрированные случайные величины (см. гл. VIII, § 2), корреляционный момент можно определить как математическое ожидание произведения центрированных случайных величин: μху=M[ 3амечание 2. Легко убедиться, что корреляционный момент можно записать в виде μху=M (XY) -M (X) M (Y). Теорема 1. Корреляционный момент двух независимых случайных величин X и Y равен нулю. Доказательство. Так как X и Y - независимые случайные величины, то их отклонения X - М (X)и Y - М (Y)также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим μху= М {[Х - М (X) ][Y - M (Y) ]} = М [Х-М (X) ]M[Y - M (Y) ]= 0. Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины. Пусть, например, X и Y были измерены в сантиметрах и μху = 2 см2; если измерить X и Y в миллиметрах, то μху = 200мм. Такая особенность корреляционного момента является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того чтобы устранить этот недостаток, вводят новую числовую характеристику - коэффициент корреляции.
Коэффициентом корреляции rху случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин: rху= μху/ (σx σy). (*) Так как размерность μху равна произведению размерностей величин X и Y, σх имеет размерность величины X, σy имеет размерность величины Y (см. гл. VIII, § 7), то rху - безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом. Очевидно, коэффициент корреляции независимых случайных величин равен нулю (так как μху = 0). Замечание 3. Во многих вопросах теории вероятностей целесообразно вместо случайной величины X рассматривать нормированную случайную величину X’, которую определяют как отношение отклонения к среднему квадратическому отклонению: X’= (X-M (X)) / σx. Нормированная величина имеет математическое ожидание, равное нулю, и дисперсию, равную единице. Действительно, используя свойства математического ожидания и дисперсии, имеем:
Легко убедиться, что коэффициент корреляции rху равен корреляционному моменту нормированных величин X’ и Y’:
Теорема 2. Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий:
Доказательство. Введем в рассмотрение случайную величину Z 1 =σyX—σxY и найдем ее дисперсию D (Z 1) = M[Z 1 —mz] 2. Выполнив выкладки, получим D (Z 1) = 2 Любая дисперсия неотрицательна, поэтому 2 Отсюда μху ≤ σx σy. (**) Введя случайную величину Z 1 =σvX +σxY, аналогично найдем μху≥ - σx σy. (***) Объединим (**) и (***): - σx σy≤ μху ≤ σx σy, (****) или
Итак,
Теорема 3. Абсолютная величина коэффициента корреляции не превышает единицы: rху ≤1. Доказательство: Разделим обе части двойного неравенства (****) на произведение положительных чисел σx σy - 1 ≤ rху ≤ 1. Итак, rху≤ 1.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.131.35 (0.011 с.) |

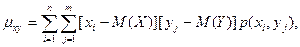

 ].
].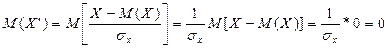 ;
; .
.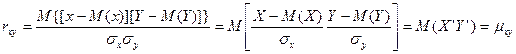 .
.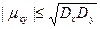
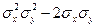 μху.
μху. .
.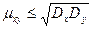 .
.


