
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционная функция производной стационарной случайной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Теорема. Корреляционная функция производной X' (t) =
Доказательство. Известно, что корреляционная функция производной любой дифференцируемой случайной функции равна второй смешанной производной от ее корреляционной функции (см. гл. XXIII, § 16, теорема 2):
По условию, X (t) — стационарная функция, поэтому ее корреляционная функция зависит только от разности аргументов:
Из соотношения τ = t 2- t 1 следует,что
Учитывая равенства (*), получим
Видим, что искомая корреляционная функциязависиттолько от τ, поэтому
Итак,
Пример. Задана, корреляционная функция kx (τ) = Решение, а) Продифференцировав дважды заданную корреляционную функцию и изменив знак результата на противоположный, найдем искомую корреляционную функцию:
б) Положив τ =0, получим искомую дисперсию:
Взаимная корреляционная функция стационарной случайной функции и ее производной Теорема. Взаимная корреляционная функция дифференцируемой стационарной случайной функции Х′ (t) и ее производной X' (t) =x равна первой производной от корреляционной функции kx (τ), взятой со своим (противоположным) знаком, если индекс а) Предполагается, что τ = t 2- t 1 Доказательство. а) По Определениювзаимнойкорреляционной функции,
Операции нахождения математического ожидания и дифференцирования можно переставить (см. гл. XXIII, § 16, замечание 1), поэтому
Так как X (t) — стационарная функция, то ее корреляционная функция зависит только от разности аргументов:
Правая часть равенства зависит только от τ; следовательно, и левая часть есть функция от τ. Обозначив ее через
б) Доказывается аналогично. Заметим, что поскольку взаимная корреляционная функция Пример. Задана корреляционная функция Решение. Воспользуемся формулой
а) Пусть τ ≥0. Тогда | τ |= τ,
б) Пусть τ<0. Тогда |τ|=-τ,
Итак, искомая взаимная корреляционная функция
Корреляционная функция интеграла от стационарной случайной функции Теорема. Корреляционная функция интеграла
Доказательство. Известно, что корреляционная функция интеграла
Принимая во внимание, что корреляционная функция стационарной случайной функции зависит только от разности аргументов, т. е.
Вычисление этого интеграла весьма громоздко, поэтому ограничимся указаниями: перейти к новым переменным τ = s 2 – s 1, ξ= s 2+ s 1;
начертить новую область интегрирования, ограниченную прямыми τ =ξ, τ =-ξ, τ =ξ-2 t 1, τ =-ξ+2 t 1и выполнить интегрирование по ξ. Двойной интеграл по области OABD можно вычислить как разность двойных интегралов по областям ОАС и BDC. При интегрировании по области ODE переставить пределы интегрирования по τ и перейтик новой переменной τ ' =- τ (рис. 28). Следствие. Дисперсия интеграла
Действительно, положив t 1= t 2= t в формуле (*), получим
После приведения подобных членов окончательно имеем
Пример. Задана корреляционная функция kx (t)=l/(1+τ2) стационарной случайной функции Х (t). Найти дисперсию интеграла Решение. Воспользуемся формулой (**);
Выполнив интегрирование, получим искомую дисперсию: Dy (t)=2 t arc t g t — ln(1 + t 2)• Заметим, что функция Y (t) не стационарна, так как ее дисперсия не постоянна, а зависит от аргумента t.
Определение характеристик аргодическях стационарных случайных Функций из опыта Среди стационарных случайных функций можно выделить класс функций, оценка характеристик которых путем усреднения множества реализации равносильна усреднению по времени только одной реализации достаточно большой длительности. Стационарную случайную функцию X (t) называют аргодической, если ее характеристики, найденные усреднением множества реализации, совпадают с соответствующими характеристиками, полученными усреднением по времени одной реализации x (t), которая наблюдалась на интервале (0, Т) достаточно большой длительности. Достаточное условие эргодичности стационарной случайной функции Х (t) относительно математического ожидания состоит в том, что ее корреляционная функция kx (τ) при τ→∞ стремится к нулю:
Достаточное условие эргодичности стационарной случайной функции Х (t) относительно корреляционной функции состоит в том, что корреляционная функция ky (τ) при τ→∞ стремится к нулю:
где В качестве оценки математического ожидания эргодической стационарной случайной функции Х (t) по наблюдавшейся на интервале (0, T) реализации x (t) принимают среднее по времени ее значение:
Известно, что корреляционная функция стационарной случайной функции
Таким образом, оценить kx (τ) означает оценить математическое ожидание функции Итак, в качестве оценки корреляционной функции эргодической стационарной случайной функции принимают
либо,что равносильно,
Практически интегралы вычисляют приближенно, например по формуле прямоугольников. С этой целью делят интервал (0, Т) на п частичных интервалов длиной Δ t = Т/п; в каждом частичном i -м интервале выбирают одну точку, например его середину ti. В итоге оценка (*) принимает вид
Учитывая, что Δ t=T/n, окончательно получим
Аналогично приближенно вычисляют интеграл (**), полагая, что τ принимает значения Δ t, 2Δ t,…,(n -1) Δ t, или, что то же, T/n,2 T/n, 3T/n, …,(n- 1) T/n. В итоге оценки корреляционной функции (**) и (***) принимают соответственно вид:
где l= 1, 2,..., n—1. Замечание. Можно показать, что оценка (*)—несмещенная, т.е. М [ mx *]= mx; оценка (**)—асимптотически несмещенная, т.е.
Задачи 1. Является ли стационарной случайная функция Х (t)= t 3 U, где U —случайная величина, причем: а) ти≠ 0, б) ти =0? Отв. а) Нет: тх (t)≠cons t; б) Нет: корреляционная функция зависит не от разности аргументов, а от каждого из них. 2. Стационарна ли случайная функция Х (t)=sin(t + φ), где φ —случайная величина, распределенная равномерно в интервале (0,2π)? Отв. Да: тх(t)=0=const. K.x(t1,t2)=0,5cos(t2 - t1). 3. Известно, что если φ —случайная величина, распределенная равномерно в интервале (0,2 π), то случайная функция Х (t) =s in(t + φ)—стационарная. Можно ли отсюда непосредственно заключить, что случайная функция Y (t)=cos(t + φ) также стационарна? Отв. Можно: изменив начало отсчета аргумента, напримерна π /2, стационарной функции Х (t), получим функцию Y (t). 4. Задана случайная функция Х (t)= t+U sin t+Vcost, где U и V— случайные величины, причем М (U) =M (V)=0, D (U) =D (V)=5, M (UV) =0. Доказать, что: а) Х (t) — нестационарная функция; б) X (t)—стационарная функция. Отв. а) тх (t)≠cons t; б) 5. Известна корреляционная функция kx (τ)= Отв. 6. Задана корреляционная функция kx (τ)= Отв. 7. Заданы две стационарные случайные функции Х (t) =cos (2 t + φ) и Y(t)=sin(2 t + φ), где φ —случайная величина, распределенная равномерно в интервале (0, 2 π). Доказать, что заданные функции стационарно связаны. Отв. Rxy(t1,t2)=0,5sin2(t2 – t1). 8. Задана корреляционная функция Отв. a) 9. Задана корреляционная функция Отв.. 10. Задана корреляционная функция Отв. D у(t)=2(t +е- t - 1).
Глава двадцать пятая
|
|||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 дифференцируемой стационарной случайной функции Х (t) равна второй производной от ее корреляционной функции, взятой со знаком минус:
дифференцируемой стационарной случайной функции Х (t) равна второй производной от ее корреляционной функции, взятой со знаком минус: .
. 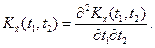 '
'
 и
и 



 стационарной случайной функции Х (t). Найти: а) корреляционную функцию; б) дисперсию производной X' (t) =
стационарной случайной функции Х (t). Найти: а) корреляционную функцию; б) дисперсию производной X' (t) =  .
.

 б)
б) 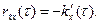


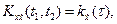 где τ = t 2- t 1 и, следовательно,
где τ = t 2- t 1 и, следовательно,  Таким образом,
Таким образом,
 окончательно получим
окончательно получим
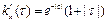 стационарной случайной функции X (t). Найти взаимную корреляционную функцию
стационарной случайной функции X (t). Найти взаимную корреляционную функцию  заданной случайной функции и ее производной.
заданной случайной функции и ее производной.

 Таким образом,при τ≥ 0
Таким образом,при τ≥ 0

 . Таким образом, при τ<0
. Таким образом, при τ<0

 от стационарной случайной функции равна
от стационарной случайной функции равна
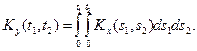
 получим
получим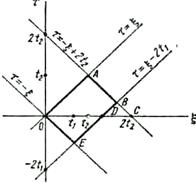

 (**)
(**)


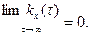


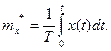 (*)
(*)
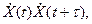 поэтому можно воспользоваться соотношением (*), учитывая, что функция
поэтому можно воспользоваться соотношением (*), учитывая, что функция  определена при t+τ≤T и, следовательно, t≤T - τ.
определена при t+τ≤T и, следовательно, t≤T - τ. (**)
(**) (***)
(***)
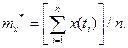
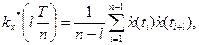

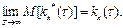
 Kx (t 1, t 2)=5cos(t 2 - t 1).
Kx (t 1, t 2)=5cos(t 2 - t 1).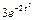 стационарной случайной функции Х (t). Найти корреляционную функцию случайной функции Y (t) = 5 X (t).
стационарной случайной функции Х (t). Найти корреляционную функцию случайной функции Y (t) = 5 X (t). .
. стационарной случайной функции Х (t). Найти нормированную корреляционную функцию.
стационарной случайной функции Х (t). Найти нормированную корреляционную функцию.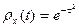 .
. стационарной случайной функции Х (t). Найти: а) корреляционную функцию; б) дисперсию производной X ′(t) =
стационарной случайной функции Х (t). Найти: а) корреляционную функцию; б) дисперсию производной X ′(t) =  ; б)
; б) 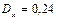 .
. стационарной случайной функции Х (t). Найти взаимные корреляционные функции случайной функции Х (t) и ее производной.
стационарной случайной функции Х (t). Найти взаимные корреляционные функции случайной функции Х (t) и ее производной. ;
; 
 стационарной случайной функции Х (t). Найти дисперсию интеграла
стационарной случайной функции Х (t). Найти дисперсию интеграла 


