
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплексные случайные функции и их характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Комплексной слуюйной функцией называютфункцию Z (t) =X (t) +Y (t) i, где Х (t) и Y (t)—действительные случайные функции действительного аргумента t. Обобщим определения математического ожидания и дисперсии на комплексные случайные функции так, чтобы, в частности, при Y=0 эти характеристики совпали с ранее введенными характеристиками для действительных случайных функций, т. е. чтобы выполнялись требования: mz (t) =mx (t)(*) Dz (t) =Dx (t)(**) Математическим, ожиданием, комплексной случайной функции Z (t)= Х (t) +Y (t) i называют комплексную функцию (неслучайную) mz (t) =mx (t) +my (t) i. В частности, при Y=0 получим тz (t) =тx (t),т.е. требование (*) выполняется. Дисперсией комплексной случайной функции Z (t) называют математическое ожидание квадрата модуля центрированной функции Z (t): Dz (t) =M [| В частности, при Y==0 получим Dz(t) = M [| Учитывая, что математическое ожидание суммы равно сумме математических ожиданий слагаемых, имеем Dz (t) =M [| Итак, дисперсия комплексной случайной функции равна сумме дисперсий ее действительной и мнимой частей: Dz (t) =Dx (t) +Dy (t). Известно, что корреляционная функция действительной случайной функции Х (t) при разных значениях аргументов равна дисперсии Dx (t). Обобщим определение корреляционной функции на комплексные случайные функции Z (t) так, чтобы при равных значениях аргументов t 1 =t 2 =t корреляционная функция Kz (t, t) была равна дисперсии Dz (t), т. е. чтобы выполнялось требование Kz (t, t) =Dz (t). (***) Корреляционной функцией комплексной случайной функции Z (t) называют корреляционный момент сечений Kz (t 1, t 2) = M [ В частности, при равных значениях аргументов Kz (t, t) = M [
т. е. требование (***) выполняется. Если действительные случайные функции Х (t) и Y (t)коррелированы, то Kz (t 1, t 2) = Kx (t 1, t 2) +Ky (t 1, t 2) + [ Rxy (t 2, t 1)] + [ Rxy (t 1, t 1)]. если Х (t) и Y (t) не коррелированы, то Kz (t 1, t 2) = Kx (t 1, t 2) +Ky (t 1, t 2). Рекомендуем убедиться в справедливости этих формул, используя соотношение (****) предыдущего параграфа. Обобщим определение взаимной корреляционной функции на комплексные случайные функции Z 1(t)= Х 1(t)+ Y 1(t) i и Z 2(t)= Х 2(t)+ Y 2(t) i так, чтобы, в частности, при Y 1 =Y 2 = 0 выполнялось требование
Взаимной корреляционной функцией двух комплексных случайных функций называют функцию (неслучайную)
В частности, при Y 1 =Y 2=0 получим
т. е. требование (****) выполняется. Взаимная корреляционная функция двух комплексных случайных функций выражается через взаимные корреляционные функции их действительных и мнимых частей следующей формулой:
Рекомендуем вывести эту формулу самостоятельно. Задачи 1. Найти математическое ожидание случайных функций: a) X (t) =Ut 2, где U— случайная величина, причем M (U) =5, б) Х (t) =U cos2 t+Vt, где U и V— случайные величины, причем M (U) =3, M (V) =4. Отв. а) mx(t)=5t2; б) тx(t)=3 cos2t+4t. 2. Задана корреляционная функция Кх (t 1, t 2) случайной функции X (t). Найти корреляционные функции случайных функций: a) Y (t) =X (t) +t; б) Y (t)=(t +1) X (t); в) Y (t) =4X (t). Отв. a) Кy(t1,t2)= Кх(t1,t2); б) Кy(t1,t2)=(t1+1)(t2+1) Кх(t1,t2); в) Кy(t1,t2)=16 Кx(t1,t2)=. 3. Задана дисперсия Dx (t) случайной функции Х (t). Найти дисперсию случайных функций: a) Y (t) =Х (t) +et б) Y (t) =tX (t). Отв. a) Dy (t) =Dx (t); б) Dy (t) =t 2 Dx (t). 4. Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию случайной функции Х (t)= Usin 2 t, где U— случайная величина, причем M (U) =3, D (U) =6. Отв. а) mx (t) =3 sin 2 t; б) Кх (t 1, t 2)= 6 sin 2 t 1 sin 2 t 2; в) Dx (t)=6 sin 22 t. 5. Найти нормированную корреляционную функцию случайной функции X (t), зная ее корреляционную функцию Кх (t 1, t 2)=3 cos (t 2 —t 1). Отв. ρx(t1,t2)=cos(t2-t1). 6. Найти: а) взаимную корреляционную функцию; б) нормированную взаимную корреляционную функцию двух случайных функций X (t)=(t +1) U, и Y(t) = (t 2 + 1) U, где U— случайная величина, причем D (U)=7. Отв. a) Rxy (t 1, t 2)=7(t 1+l)(t 22+l); б) ρxy (t 1, t 2)=1. 7. Заданы случайные функции Х (t) = (t— 1) U и Y (t)= t 2 U, где U и V — некоррелированные случайные величины, причем M (U)=2, M (V) = 3, D (U) =4, D (V) =5. Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию суммы Z (t) =X (t) +Y (t). Указание. Убедиться, что взаимная корреляционная функция заданных случайных функций равна нулю и, следовательно, Х (t) и Y (t) не коррелированы. Отв. а) mz (t)=2(t - 1)+3 t 2; б) Кz (t 1, t 2)=4(t 1 - l)(t 2- 1)+6 t 12 t 22; в) Dz (t)=4(t - 1)2+6 t4. 8. Задано математическое ожидание mx (t)= t 2+1 случайной функции Х (t). Найти математическое ожидание ее производной. Отв. 9. Задано математическое ожидание mx (t) =t 2 +3 случайной функции Х (t). Найти математическое ожидание случайной функции Y (t) =tХ' (t) +t3. Отв. my(t)=t2(t+2). 10. Задана корреляционная функция Кх (t 1, t 2)= Отв. 11. Задана корреляционная функция Кх (t 1, t 2)= a) Отв. a) 12. Задано математическое ожидание mx (t)=4 t3 случайной функции Х (t). Найти математическое ожидание интеграла Отв. my(t)=t4. 13. Задана случайная функция Х (t) =Ucos 2 t, где U— случайная величина, причем M (U) = 2. Найти математическое ожидание случайной функции Отв. ту (t) =(t 2+1)[ t+ (sin 2 t)/2].
14. Задана корреляционная функция Кx (t 1, t 2) =cosωt 1 cosωt 2 случайной функции Х (t). Найти: а) корреляционную функцию; б) дисперсию интеграла Отв. a) 15*. Задана случайная функция Х (t) =Ue3tcos 2 t, где U— случайная величина, причем М (U) = 5, D (U)=1. Найти: а) математическое ожидание, б) корреляционную функцию, в) дисперсию интеграла Отв. а) mx(t)=5е3tcos2t; в) 16. Задана корреляционная функция Кх (t 1, t 2)= t 1 t 22 случайной функции Х (t). Найти взаимные корреляционные функции: a) Rxy (t 1, t 2); б ) Ryx (t 1, t 2) случайных функций Х (t) и Отв. a) Rxy(t1,t2)=t1t23/3; б) Ryx (t1,t2)=t12t22/2. Глава двадцать четвертая
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (t)|2].
(t)|2].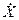 (t)|] 2 =Dx (t), т. е. требование (**) выполняется.
(t)|] 2 =Dx (t), т. е. требование (**) выполняется. (t)2]}= M [
(t)2]}= M [ 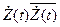 ].
]. (****)
(****)


 .
. случайной функции X (t). Найти корреляционную функцию ее производной.
случайной функции X (t). Найти корреляционную функцию ее производной.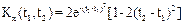 .
. б)
б) 
 б)
б)  .
. .
. .
. Dy(t)=(sin2ωt)/ω2.
Dy(t)=(sin2ωt)/ω2.




