Групповая, внутригрупповая, межгрупповая и общая дисперсии
Похожие статьи вашей тематики
Допустим, что все значения количественного признака X совокупности, безразлично-генеральной или выборочной, разбиты на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти групповую среднюю (см. § 6) и дисперсию значений признака, принадлежащих группе, относительно групповой средней.
Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней
 , ,
где ni - частота значения xi; j - номер группы; 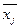 - групповая средняя группы j; - групповая средняя группы j;  - объем группы j. - объем группы j.
Пример 1. Найти групповые дисперсии совокупности, состоящей из следующих двух групп:
| первая группа
|
| вторая группа
| |
| xi
| ni
|
|
| xi
| ni
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| 
| 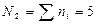
| Решение. Найдем групповые средние:
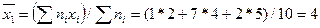 ; ;
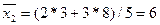 . .
Найдемискомые групповые дисперсии:
 ; ;
 . .
Зная дисперсию каждой группы, можно найти их среднюю арифметическую.
Внутригрупповой дисперсией называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
 , ,
где Nj - объем группы j; п =  - объем всей совокупности. - объем всей совокупности.
Пример 2. Найти внутригрупповую дисперсию по данным примера 1.
Решение. Искомая внутригрупповая дисперсия равна
 
Зная групповые средние и общую среднюю, можно найти дисперсию групповых средних относительно общей средней.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
 , ,
где 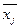 - групповая средняя группы j; Nj - объем группы j; - групповая средняя группы j; Nj - объем группы j;  - общая средняя; n = - общая средняя; n =  - объем всей совокупности. - объем всей совокупности.
Пример 3. Найти межгрупповую дисперсию по данным примера 1.
Решение. Найдем общую среднюю:
 . .
Используя вычисленные выше величины  = 4, = 4,  = 6, найдем искомую межгрупповую дисперсию: = 6, найдем искомую межгрупповую дисперсию:
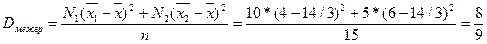 . .
Теперь целесообразно ввести специальный термин для дисперсии всей совокупности.
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:
 , ,
где ni - частота значения xi;  - общая средняя; n - объем всей совокупности. - общая средняя; n - объем всей совокупности.
Пример 4. Найти общую дисперсию по данным примера 1.
Решение. Найдем искомую общую дисперсию, учитывая, что общая средняя равна 14/3:

Замечание. Найденная общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
D общ= 148/45;
D внгр + D межгр= 12/5 + 8/9= 148/45.
В следующем параграфе будет доказано, что такая закономерность справедлива для любой совокупности.
Сложение дисперсий
Теорема. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой имежгрупповой дисперсий:
D общ =D внгр + D межгр.
Доказательство. Для упрощения доказательства предположим, что вся совокупность значений количественного признака X разбита на две следующие группы:
| Группа……………………
| первая
|
| вторая
| | Значение признака………..
| x 1 x 2
| x 1 x 2
| | Частота…………………….
| m 1 m 2
| n 1 n 2
| | Объем группы…………….
| N 1 = m 1 + m 2
| N 2 = n 1 + n 2
| | Групповая средняя……….
| 
| 
| | Групповая дисперсия…….
| 
| 
| | Объем своей совокупности
| n=N 1 +N 2
|
Далее для удобства записи вместо знака суммы  пишется знак пишется знак  . .
Например,  . .
Следует также иметь в виду, что если под знаком суммы стоит постоянная величина, то ее целесообразно выносить за знак суммы.
Например,  . .
Найдем общую дисперсию:
D общ=  . (*) . (*)
Преобразуем первое слагаемое числителя, вычтя и прибавив  : :

 . .
Так как
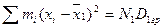
(равенство следует из соотношения 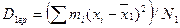 ) и в силу § 7 ) и в силу § 7
 , ,
тo первое слагаемое принимает вид
 . (**) . (**)
Аналогично можно представить второе слагаемое числителя (*) (вычтя и прибавив  ): ):
 . (***) . (***)
Подставим (**) и (***) в (*):
 . .
Итак,
D общ =D внгр + D межгр.
Пример, иллюстрирующий доказанную теорему, приведен в предыдущем параграфе.
Замечание. Теорема имеет не только теоретическое, но и важное практическое значение. Например, если в результате наблюдений получены несколько групп значений признака, то для вычисления общей дисперсии можно группы в единую совокупность не объединять. С другой стороны, если совокупность имеет большой объем, то целесообразно разбить ее на несколько групп. В том и другом случаях непосредственное вычисление общей дисперсии заменяется вычислением дисперсий отдельных групп, что облегчает расчеты.
|