Выборочное корреляционное отношение
Похожие статьи вашей тематики
Для оценки тесноты линейной корреляционной связи между признаками в выборке служит выборочный коэффициент корреляции. Для оценки тесноты нелинейной корреляционной связи вводят новые сводные характеристики:
ηyx — выборочное корреляционное отношение Y к X;
ηxy —выборочное корреляционное отношение Х к Y.
Выборочным корреляционным отношением Y к Х называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:
ηyx = σмежгр/σобщ,
или в других обозначениях
 . .
Здесь
 ; ;
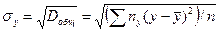 , ,
где n—объем выборки (сумма всех частот); nx—частота значения х признака X; ny—частота значения у признака Y; 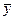 —общая средняя признака Y; —общая средняя признака Y;  —условная средняя признака У. —условная средняя признака У.
Аналогично определяется выборочное корреляционное отношение Х к Y:
 . .
Пример. Найти ηyx по данным корреляционной табл. 18. Таблица 18
| у
| X
| |
|
|
| ny
| |
|
|
|
|
| |
|
| —
|
|
| | nx
|
|
|
| n=50
| 
|
|
|
|
| Решение. Найдем общую среднюю:
 = (38·15+12·25)/50= 17,4. = (38·15+12·25)/50= 17,4.
Найдем общее среднее квадратическое отклонение:
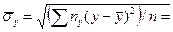
 . .
Найдем межгрупповое среднее квадратическое отклонение:

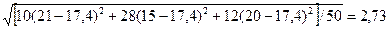 . .
Искомое корреляционное отношение
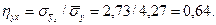
Свойства выборочного корреляционного отношения
Поскольку ηxy обладает теми же свойствами, что и ηyx, перечислим свойства только выборочного корреляционного отношения ηyx, которое далее для упрощения записи будем обозначать через η и для простоты речи называть «корреляционным отношением».
Свойство 1. Корреляционное отношение удовлетворяет двойному неравенству
0≤ η ≤1.
Доказательство. Неравенство η≥0 следует из того, что η есть отношение неотрицательных чисел— средних квадратических отклонений (межгруппового к общему).
Для доказательства неравенства η≤1 воспользуемся формулой
Dобщ = Dвнгр + Dмежгр
Разделив обе части равенства на Dобщ получим
1 = Dвнгр / Dобщ + Dмежгр/ Dобщ,
или
1 = Dвнгр / Dобщ + η2.
Так как оба слагаемых неотрицательны и сумма их равна единице, то каждое из них не превышает единицы; в частности, η2≤1. Приняв во внимание, что η≥0, заключаем:
0≤ η ≤1.
Свойство 2. Если η=0, то признак Н с признаком Х корреляционной зависимостью не связан. Доказательство. По условию,
η = σмежгр/σобщ=0.
Отсюда σмежгр = 0 и, следовательно, Dмежгр = 0.
Межгрупповая дисперсия есть дисперсия условных (групповых) средних  относительно общей средней относительно общей средней 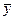 . Равенство нулю межгрупповой дисперсии означает, что при всех значениях Х условные средние сохраняют постоянное значение (равное общей средней). Иными словами, при η=0 условная средняя не является функцией от X, а значит, признак Y не связан корреляционной зависимостью с признаком X. . Равенство нулю межгрупповой дисперсии означает, что при всех значениях Х условные средние сохраняют постоянное значение (равное общей средней). Иными словами, при η=0 условная средняя не является функцией от X, а значит, признак Y не связан корреляционной зависимостью с признаком X.
Замечание 1. Можно доказать и обратное предложение: если признак Y не связан с признаком Х корреляционной зависимостью, η=0.
Свойство 3. Если η=1, то признак Y связан с признаком Х функциональной зависимостью.
Доказательство. По условию,
η = σмежгр/σобщ=1.
Отсюда
σмежгр=σобщ.
Возведя обе части равенства в квадрат, получим
Dобщ = Dмежгр. (*)
Так как Dобщ = Dвнгр + Dмежгр, то в силу (*)
Dвнгр = 0. (**)
Поскольку внутригрупповая дисперсия есть средняя арифметическая групповых дисперсий (взвешенная по объемам групп), то из (**) следует, что дисперсия каждой группы, (значений Y, соответствующих определенному значению X) равна нулю. А это означает, что в группе содержатся равные значения Y, т. е. каждому значению Х соответствует одно значение V. Следовательно, при η=1 признак Y связан с признаком Х функциональной зависимостью.
Замечание 2. Можно доказать и обратное предположение:
если признак Y связан с признаком Х функциональной зависимостью, то η=1.
Приведем еще два свойства, опустив доказательства. Свойство 4. Выборочное корреляционное отношениене меньше абсолютной величины выборочного коэффициента корреляции: η≥|rв|.
Свойство 5. Если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, то имеет место точная линейная корреляционная зависимость.
Другими словами, если η=|rв|, то точки (х1, у1), (x2, y2),..., (xn, yn) лежат на прямой линии регрессии, найденной способом наименьших квадратов.
|