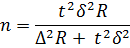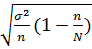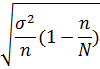Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Выборочное наблюдениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Недостающим элементом в формуле n= σ +σ2 Δ Δ2 (1− n / N) (N-1)
Недостающим элементом в формуле n=
σ σ2 Δ +Δ2 (1− n / N) (N-1)
Недостающим элементом в формуле n=
σ +σ2 Δ Δ2 (1− n / N) (N-1)
Репрезентативность результатов выборочного наблюдения зависит от +вариации признака и объема выборки определения границ объекта исследования Времени проведения наблюдения Продолжительности проведения наблюдения
Для расчета средней ошибки выборки используют формулу наличии высокого уровня вариации признака изучении качественных характеристик явлений +малой выборке уточнении данных сплошного наблюдения
Cредняя ошибка случайной повторной выборки..., если ее объем уве- личить в 4 раза: +уменьшится в 2 раза Увеличится в 4 раза Уменьшится в 4 раза Не изменится
Недостающим элементом формулы предельной ошибки случайной выборки при бесповторном отборе является: + t t2 n2 n N
Средняя ошибка выборки (μ) для средней величины характеризует вариацию признака тес ноту связи между двумя факторами +среднюю величину всех возможных расхождений выборочной и гене- ральной средней Среднее значение признака темп роста
Под выборочным наблюдением понимают: сплошное наблюдение всех единиц совокупности несплошное наблюдение части единиц совокупности +несплошное наблюдение части единиц совокупности, отобранных слу- чайным способом наблюдение за единицами совокупности в определенные моменты времени обследование наиболее крупных единиц изучаемой совокупности
Недостающим элементом в формуле дисперсии доли для генеральной совокупности является р m M +W
Пропорция отбора в выборочную совокупность при механической вы- борке определяется: +соотношением объемов выборочной и генеральной совокупностей уровнем вероятности методом отбора
Способ собственно-случайного отбора в выборочную совокупность за- ключается в отборе из генеральной совокупности: каждой десятой единицы совокупности +без какой либо системности в зависимости от уровня вероятности
Необходимая численность серийной выборки при бесповторном отбо- ре определяется по формуле:
Для оценки результатов малой выборки пользуются: критерием Фишера +критерием Стъюдента ничем не пользуются
Недостающим элементов в формуле предельной ошибки выборки для доли при бесповторном отборе является: +n N W σ
Для получения предельной ошибки выборки необходимо умножить среднюю ошибку выборки на: +коэффициент доверия численность выборочной совокупности численность генеральной совокупности
По формуле определяется ошибка выборки: средняя повторная +средняя бесповторная предельная повторная предельная бесповторная
При случайном бесповторном отборе средняя ошибка выборки опре- деляется по формуле:
Выборка называется малой, если ее объем составляет менее: 40 единиц +30 единиц 100 единиц 150 единиц
Выборка заключающаяся в отборе единиц из общего списка единиц генеральной совокупности через равные интервалы в соответствии с установленным процентом отбора называется: типической +механической случайной повторной
Для использования выборочной совокупности для дальнейшего анали- за развития социально-экономического явления необходимо, чтобы разница между средним значением генеральной совокупности и сред- ним значением выборочной совокупности была не более ошибки вы- борки: средней индивидуальной +предельной генеральной
Тема 6. Методы изучения взаимосвязи социально-экономических яв- Лений Между различными явлениями и их признаками выделяют два типа связей: функциональная и жестко детерминированная +функциональная и статистическая стохастически детерминированная и вероятностная
Функциональной называется связь, при которой: +каждому значению признака-фактора соответствует вполне определенное значение результативного признака каждому значению признака-фактора соответствует распределение значений результативного признака
В зависимости от направления действия функциональные и статисти- ческие связи могут быть: прямолинейные и криволинейные +прямые и обратные однофакторные и многофакторные
По аналитическому выражению функциональные и статистические связи могут быть: +прямолинейные и криволинейные прямые и обратные однофакторные и многофакторные
По количеству факторов, действующих на результативный признак статистические связи могут быть: прямолинейные и криволинейные прямые и обратные +однофакторные и многофакторные
Линейный коэффициент корреляции может быть: +как положительной, так и отрицательной величиной только положительной величиной только отрицательной величиной
В линейном уравнении коэффициент регрессии (а) показывает: тесноту связи долю дисперсии «у», зависимую от «х» +на сколько в среднем изменится «у» при изменении «х» на одну едини- цу ошибку коэффициента корреляции на сколько % изменится «у» при изменении «х» на 1 %
С помощью корреляционного анализа можно: +измерить тесноту связи между варьирующими признаками установить степень влияния независимых переменных на зависимую
С помощью регрессионного анализа можно: измерить тесноту связи между варьирующими признаками +установить степень влияния независимых переменных на зависимую
С помощью коэффициентов ассоциации и контингенции устанавли- вается связь между признаками: только количественными +только качественными количественными и качественными
Коэффициенты ассоциации и контингенции изменяются: от 0 до 1 +от -1 до +1 от -1 до 0
Коэффициенты взаимной сопряжённости Пирсона и Чупрова изме- няются: +от 0 до 1 от -1 до +1 от -1 до 0
Коэффициенты корреляции рангов Фехнера и Спирмена изменяются: от 0 до 1 +от -1 до +1 от -1 до 0
Коэффициент эластичности показывает: тесноту связи долю дисперсии «у», зависимую от «х» на сколько в среднем изменится «у» при изменении «х» на одну едини- цу ошибку коэффициента корреляции +на сколько % изменится «у» при изменении «х» на 1 %
Коэффициент корреляциирангов Кендалла изменяется: от 0 до 1 +от -1 до +1 от -1 до 0
Тесноту связи между альтернативными признаками можно оценить непараметрическими методами через: +коэффициенты ассоциации и контингенции показатели взаимной сопряженности Пирсона и Чупрова коэффициент корреляции рангов Кендалла
Для аналитического выражения нелинейной связи между факторами используется формула:
Наиболее тесную связь показывает коэффициент корреляции… rxy= 0,982 +rxy=- -0,991 rxy= 0,870
Обратную связь между признаками показывает коэффициент корреляции… rxy= 0,982 +rxy=- -0,991 rxy= 0,870
Эмпирическое корреляционное отношение представляет собой корень квадратный из отношения... дисперсии(й) средней из групповых дисперсий к общей +межгрупповой дисперсии к общей межгрупповой дисперсии к средней из групповых средней из групповых дисперсий к межгрупповой
Теснота связи двух признаков при нелинейной зависимости определя- ется по формуле
Корреляционный анализ используется для изучения +взаимосвязи явлений развития явления во времени структуры явлений
Тесноту связи между двумя альтернативными признаками можно из- мерить с помощью коэффициентов знаков Фехнера корреляции рангов Спирмена +ассоциации и контингенции
Парный коэффициент корреляции показывает тесноту +линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель связи между результативным признаком и остальными, включенными в модель нелинейной зависимости между двумя признаками
Парный коэффициент корреляции может принимать значения от 0 до 1 от -1 до 0 +от -1 до +1
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 2006; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.15.124 (0.007 с.) |


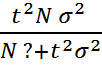
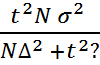
 при
при
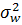 =.... (1− W)
=.... (1− W)