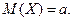Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события

 

Пусть по достаточно большому числу n независимых испытаний, в каждом из которых вероятность р появления события постоянна, но неизвестна, найдена относительная частота т/п. Пусть имеются основания предполагать, что неизвестная вероятность равна гипотетическому значению р_o. Требуется при заданном уровне значимости а проверить нулевую гипотезу, состоящую в том, что неизвестная вероятность р равна гипотетической вероятности р_а.

Поскольку вероятность оценивается по относительной частоте, рассматриваемую задачу можно сформулировать и так: требуется установить, значимо или незначимо различаются наблюдаемая относительная частота и гипотетическая вероятность.

В качестве критерия проверки нулевой гипотезы примем случайную величину

,

где q_o= 1— р_o.

Величина U при справедливости нулевой гипотезы распределена приближенно нормально с параметрами M (U) = 0, σ (U) = 1.

Пояснение. Доказано (теорема Лапласа), что при достаточно больших значениях п относительная частота имеет приближенно нормальное распределение с математическим ожиданием р и средним квадратическим отклонением . Нормируя относительную частоту (вычитая математическое ожидание и деля на среднее квадратическое отклонение), получим

,

причем M (U) = 0, σ (U) = 1.

При справедливости нулевой гипотезы, т. е. при р = р_o,

Замечание 1. Далее наблюдаемая частота обозначается через т/п в отличие от случайной величины М/п.

Поскольку здесь критическая область строится так же, как и в § 10, приведем лишь правила проверки нулевой гипотезы и иллюстрирующий пример.

Правило 1. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу Н_o: р = р_o о равенстве неизвестной вероятности гипотетической вероятности при конкурирующей гипотезе Н ₁ :р ≠ р_o, надо вычислить наблюдаемое значение критерия:

и по таблице функции Лапласа найти критическую точку u _кр по равенству Ф(u _кр) = (1-α)/2.

Если | U _набл | < u _кр - нет оснований отвергнуть нулевую гипотезу.

Если | U _набл | > u _кр - нулевую гипотезу отвергают.

Правило 2. При конкурирующей гипотезе Н ₁: р > р_o находят критическую точку равосторонней критической области по равенству Ф(u _кр) = (1-2α)/2.

Если U _набл < u _кр - нет оснований отвергнуть нулевую гипотезу.

Если U _набл > u _кр - нулевую гипотезу отвергают.

Правило 3. При конкурирующей гипотезе Н ₁: р < р_o находят критическую точку u _кр по правилу 2, а затем полагают границу левосторонней критической области

u _кр^’ = - u _кр -

Если U _набл > - u _кр - нет оснований отвергнуть нулевую гипотезу.

Если U _набл < - u _кр - нулевую гипотезу отвергают.

Замечание 2. Удовлетворительные результаты обеспечивает выполнение неравенства np ₀ q ₀> 9.

Пример. По 100 независимым испытаниям найдена относительная частота 0,08. При уровне значимости 0,05 проверить нулевую гипотезу Н_o: р = р_o = 0,12 при конкурирующей гипотезе Н ₁ :р ≠ 0,12.

Решение. Найдем наблюдаемое значение критерия

По условию, конкурирующая гипотеза имеет вид р ≠ р_o, поэтому критическая область двусторонняя.

Найдем критическую точку u _кр по равенству

Ф(u _кр) = (1—α)/2 = (1—0,05)/2 = 0,475.

По таблице функции Лапласа (см. приложение 2) находим u _кр = 1,96.Так как | U _набл | < u _кр оснований отвергнуть нулевую гипотезу. Другими словами, наблюдаемая относительная частота незначимо отличается от гипотетической вероятности

ЧАСТЬ ЧЕТВЕРТАЯ

МЕТОД МОНТЕ-КАРЛО. ЦЕПИ МАРКОВА

Глава двадцать первая

МОДЕЛИРОВАНИЕ (РАЗЫГРЫВАНИЕ) СЛУЧАЙНЫХ ВЕЛИЧИН МЕТОДОМ МОНТЕ-КАРЛО

Предмет метода Монте-Карло

Датой рождения метода Монте – Карло принято считать 1949 г.. когда американские ученые Н. Метрополис и С. Улам опубликовали статью «Метод Монте-Карло», в которой систематически его изложили. Название метода связано с названием города Монте – Карло, где в игорных домах (казино) играют в рулетку из простейших устройств для получения случайных чисел на использовании которых основан этот метод.

ЭВМ позволяют легко получать так называемые псев­дослучайные числа (при решении задач их применяют вместо случайных чисел); это привело к широкому внедрению метода во многие области науки и техники (статистическая физика, теория массового обслуживания, теория игр и др.). Метод Монте-Карло используют для вычис­ления интегралов, в особенности многомерных для решения систем алгебраических уравнений высокого порядка для исследования различного рода сложных систем (автоматического управления, экологических, биологических и т.д.).

Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую величину X, математическое ожидание которой равно а:

Практически же поступают так: производят п испытаний, в результате которых получают n возможных значении X, вычисляют их среднее арифметическое

и принимают х в качестве оценки (приближенного значе­ния) а* искомого числа а:

Поскольку метод Монте—Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указы­вает, как наиболее целесообразно выбрать случайную величину X, как найти ее возможные значения. В част­ности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*.

Отыскание возможных значений случайной величины X (моделирование) называют «разыгрыванием случайной ве­личины». Изложим лишь некоторые способы разыгрывания случайных величин и укажем, как оценить допускаемую при этом ошибку.