
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод наибольшего правдоподобияСодержание книги
Поиск на нашем сайте
Кроме метода моментов, который изложен в предыдущем параграфе, существуют и другие методы точечной оценки неизвестных параметров распределения. К ним относится метод наибольшего правдоподобия, предложенный Р. Фишером. А. Дискретные случайные величины. Пусть X - дискретная случайная величина, которая в результате n испытаний приняла значения х 1, х 2,..., хп. Допустим, что вид закона распределения величины X задан, но неизвестен параметр θ, которым определяется этот закон. Требуется найти его точечную оценку. Обозначим вероятность того, что в результате испытания величина X примет значение хi (i= 1, 2,..., n), через p (хi; θ). Функцией правдоподобия дискретной случайной величины X называют функцию аргумента θ: L (х 1, х 2 ,..., хп; θ) = p (х 1; θ) р (х 2; θ) ... p (хn; θ), где х 1, х 2,..., хп - фиксированные числа. В качестве точечной оценки параметра θ принимают такое его значение θ * = θ * (х 1, х 2 ,..., хп),при котором функция правдоподобия достигает максимума. Оценку θ * называют оценкой наибольшего правдоподобия. Функции L и ln L достигают максимума при одном и том же значении θ, поэтому вместо отыскания максимума функции L ищут (что удобнее) максимум функции ln L. Логарифмической функцией правдоподобия называют функцию ln L. Как известно, точку максимума функции ln L аргумента θ можно искать, например, так: 1) найти производную 2) приравнять производную нулю и найти критическую точку - корень полученного уравнения (его называют уравнением правдоподобия); 3) найти вторую производную Найденную точку максимума θ * принимают в качестве оценки наибольшего правдоподобия параметра θ. Метод наибольшего правдоподобия имеет ряд достоинств: оценки наибольшего правдоподобия, вообще говоря, состоятельны (но они могут быть смещенными), распределены асимптотически нормально (при больших значениях n приближенно нормальны) и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра θ существует эффективная оценка θ *, то уравнение правдоподобия имеет единственное решение θ *; этот метод наиболее полно использует данные выборки об оцениваемом параметре, поэтому он особенно полезен в случае малых выборок. Недостаток метода состоит в том, что он часто требует сложных вычислений. Замечание 1. Функция правдоподобия - функция от аргумента θ; оценка наибольшего правдоподобия - функция от независимых аргументов х 1, х 2,..., хп. Замечание 2. Оценка наибольшего правдоподобия не всегда совпадает с оценкой, найденной методом моментов.
Пример 1. Найти методом наибольшего правдоподобия оценку параметра λ распределения Пуассона
где m - число произведенных испытаний; xi - число появлений события в i -м (i =1, 2,..., n) опыте (опыт состоит из т испытаний). Решение. Составим функцию правдоподобия, учитывая, что. θ=λ: L =p (х 1; λ:) p (х 2; λ:)... p (хn; λ:),=
Найдем логарифмическую функцию правдоподобия:
Найдем первую производную по λ:
Напишем уравнение правдоподобия, для чего приравняем первую производную нулю:
Найдем критическую точку, для чего решим полученное уравнение относительно λ:
Найдем вторую производную по λ:
Легко видеть, что при λ = Пример 2. Найти методом наибольшего правдоподобия оценку параметра p биномиального распределения
если в n 1 независимых испытаниях событие А появилось х 1= m 1 раз и в п 2независимых испытаниях событие А появилось х 2 = т 2раз. Решение. Составим функцию правдоподобия, учитывая, что θ = p: Найдем логарифмическую функцию правдоподобия:
Найдем первую производную по р:
Напишем уравнение правдоподобия, для чего приравняем первую производную нулю: Найдем критическую точку, для чего решим полученное уравнение относительно p:
Найдем вторую производную по p:
Легко убедиться, что при
Б. Непрерывные случайные величины. Пусть X - непрерывная случайная величина, которая в результате n испытаний приняла значения х 1, х 2,..., xп. Допустим, что вид плотности распределения f (x)задан, но не известен параметр θ, которым определяется эта функция. Функцией правдоподобия непрерывной случайной величины X называют функцию аргумента θ: L (х 1, х 2,..., хп; θ) = f (х 1; θ) f (х 2; θ)... f (xn; θ), где х 1, х 2,..., xп — фиксированные числа. Оценку наибольшего правдоподобия неизвестного параметра распределения непрерывной случайной величины ищут так же, как в случае дискретной величины. Пример 3. Найти методом наибольшего правдоподобия оценку параметра λ, показательного распределения
если в результате n испытаний случайная величина X,распределенная по показательному закону, приняла значения х 1, х 2,..., хп. Решение. Составим функцию правдоподобия, учитывая, что θ= λ: L=f (х 1; λ) f (х 2; λ)... f (хn; λ) = Отсюда
Найдем логарифмическую функцию правдоподобия:
Найдем первую производную по λ:
Напишем уравнение правдоподобия, для чего приравняем первую производную нулю:
Найдем критическую точку, для чего решим полученное уравнение относительно λ:
Найдем вторую производную по λ:
Легко видеть, что при λ = 1/ Замечание. Если плотность распределения f (х)непрерывной случайной величины X определяется двумя неизвестными параметрами θ 1 и θ 2, то функция правдоподобия является функцией двух независимых аргументов θ 1 и θ 2: L=f (х 1; θ 1, θ 2) f (х 2; θ 1, θ 2)... f (хn; θ 1, θ 2), где х 1, х 2,..., хп - наблюдавшиеся значения X. Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют и решают систему
Пример 4. Найти методом наибольшего правдоподобия оценки параметров а и σ нормального распределения
если в результате n испытаний величина X приняла значения х 1, х 2,..., хп. Решение. Составим функцию правдоподобия, учитывая, что θ 1= a и θ 2=σ
Отсюда
Найдем логарифмическую функцию правдоподобия:
Найдем частные производные по а и по σ:
Приравняв частные производные нулю и решив полученную систему двух уравнений относительно а и σ2, получим:
Итак, искомые оценки наибольшего правдоподобия: а * =
§ 23. Другие характеристики вариационного ряда
Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда. Укажем главные из них. Модой М 0называют варианту, которая имеет наибольшую частоту. Например, для ряда варианта....1 4 7 9 частота.... 5 1 20 6 мода равна 7. Медианой те называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n = 2 k+ 1, то m е= xk+ 1 при четном n = 2 k медиана Например, для ряда 23567 медиана равна 5; для ряда 235679 медиана равна (5 + 6)/2 = 5,5. Размахом варьирования R называют разность между наибольшей и наименьшей вариантами: R=x max- x min Например, для ряда 1 3456 10 размах равен 10 — 1 =9. Размах является простейшей характеристикой рассеяния вариационного ряда. Средним абсолютным отклонением θ называют среднее арифметическое абсолютных отклонений:
Например, для ряда хi 1 3 6 16 ni 4 10 5 1 имеем:
Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда. Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней:
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше. Коэффициент вариации — безразмерная величина, поэтому он пригоден для сравнения рассеяний вариационных рядов, варианты которых имеют различную размерность, например если варианты одного ряда выражены в сантиметрах, а другого — в граммах. Замечание. Выше предполагалось, что вариационный ряд составлен по данным выборки, поэтому все описанные характеристики называют выборочными; если вариационный ряд составлен по данным генеральной совокупности, то характеристики называют генеральными. Задачи 1. Найти групповые средние совокупности, состоящей из двух групп: первая группа... Х{ 0,1 0,4 0,6 ni 325 вторая группа... */ 0,1 0,3 0,4 П{ 10 4 6 Отв. 2. Найти общую среднюю по данным задачи 1 двумя способами: а) объединить обе группы в одну совокупность; б) использовать найденные в задаче 1 групповые средние. Отв. 3. Дано распределение статистической совокупности: хi 1 4 5 пi 6 11 3 Убедиться, что сумма произведений отклонений на соответствующие частоты равна нулю. 4. Дано распределение статистической совокупности: xi 4 7 10 15 пi 10 15 20 5 Найти дисперсию совокупности: _а) исходя из определения дисперсии; б) пользуясь формулой D = Отв. D = 9,84. б. Найти внутригрупповую, межгрупповую и общую дисперсии совокупности, состоящей из трех групп: первая группа... Х{ 1 2 8 я/ 30 15 5 вторая группа...*/..! 6 П{ 10 15 третья группа... */ 3 8 я,- 20 5 Отв. D внгр = 4,6; D межгр=1; D общ = 5,6. 6. Найти внутригрупповую, межгрупповую и общую дисперсии совокупности, состоящей из двух групп: первая группа... Х{ 27 П (64 вторая группа... х,- 2 7 л/28 Отв. D внгр =; D межгр=1; D общ = 6. 7. Найти выборочную и исправленную дисперсии вариационного ряда, составленного по данным выборкам: варианта... 1 2 5 8 9 частота... 3 4 6 4 3 Отв: В задачах 8—9 даны среднее квадратическое отклонение, выборочная средняя и объем выборки нормально распределенного признака. Найти доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью. 8. σ = 2, 9. σ = 3, 10. Найти минимальный объем выборки, при котором с надежностью 0,95 точность оценки математического ожидания нормально распределенного признака по выборочной средней будет равна 0,2, если среднее квадратическое отклонение равно 2. Указание. См. замечание 2, § 15. Отв. n = 385. В задачах 11—12 даны «исправленное» среднее квадратическое отклонение, выборочная средняя и объем малой выборки нормально распределенного признака. Найти, пользуясь распределением Стью- дента, доверительные интервалы для оценки неизвестного математического ожидания с заданной надежностью. 11. s = 1,5, 12. s = 2,4, 13. По данным 16 независимых равноточных измерений физической величины найдены Отв. 22,948 < а < 23,374; 0,224 < σ < 0,576. 14. Найти доверительный интервал для оценки неизвестной вероятности р биномиального распределения с надежностью 0,95, если в 60 испытаниях событие появилось 18 раз. Отв. 0,200 < р < 0,424. 15. Найти методом моментов точечную оценку эксцесса Еk =m 4/σ4 - 3 теоретического распределения. Отв. еk = m 4/σ4 – 3. 16. Найти методом моментов точечные оценки параметров α и β гамма-распределения
Указание. Сделать подстановку у = х/β и, используя гаммафункцию
Отв. α* = ( 17. Найти методом наибольшего правдоподобия по выборке х 1, х 2,..., хп точечную оценку неизвестного параметра β гамма-распределения, если параметр α известен. Указание. Использовать плотность гамма-распределения, приведенную в задаче 16. Отв β* = Глава семнадцатая
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 4095; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 ;
; ; если вторая производная при θ = θ * отрицательна, то θ * - точка максимума.
; если вторая производная при θ = θ * отрицательна, то θ * - точка максимума. ,
, .
. .
. .
. .
. .
.
 вторая производная отрицательна; следовательно, λ =
вторая производная отрицательна; следовательно, λ =  ,
, .
. .
. .
. .
. .
. .
. (0< х < ∞),
(0< х < ∞), .
. .
. .
. .
. .
. .
. .
.

 .
. .
.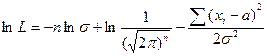 .
. ;
; 
 ;
;  .
.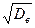 . Заметим, что первая оценка несмещенная, а вторая смещенная.
. Заметим, что первая оценка несмещенная, а вторая смещенная.
 ;
;
 .
. = 0,41;
= 0,41;  = 0,23.
= 0,23. =0,29.
=0,29. — [
— [  = 8,4; s 2 = 8,84.
= 8,4; s 2 = 8,84. .
. , найти сначала М (X)= (α+ 1) β, D (Х) = (α+1) β2, а затем приравнять М (Х) =
, найти сначала М (X)= (α+ 1) β, D (Х) = (α+1) β2, а затем приравнять М (Х) =  / Dв)— 1; β* = Dв /
/ Dв)— 1; β* = Dв / 


