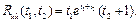Производная случайной функции и ее характеристики

При изучении случайных величин встречалось понятие сходимости по веройтности. Для изучения случайных функций необходимо ввести среднеквадратичную сходимость.

Говорят, что последовательность случайных величин X ₁, X ₂, …, Хn,... сходится в среднеквадратичном к случайной величине X, если математическое ожидание квадрата разности Х_п→Х стремится к нулю при п→∞:

M [(X_n-X)²] = 0.

Случайную величину Х называют пределом в среднеквадратичном последовательности случайных величин X ₁, X ₂, …, Хn,... и пишут

X=l. i. m. X_n.

Заметим, что из среднеквадратичной сходимости следует сходимость по вероятности; обратное утверждение, вообще говоря, неверно.

Случайную функцию Х (t) называют дифференцируемой, если существует такая функция X' (t) (ее называют производной), что

Итак, производной случайной функции Х (t) называют среднеквадратичный предел отношения приращения функции к приращению аргумента Δ t при Δ t →0:

Пусть известны характеристики случайной функции. Как найти характеристики ее производной? Ответ на этот вопрос дают теоремы, приведенные ниже, причем рассматриваются только среднеквадратично дифференцируемые случайные функции.

Теорема 1. Математическое ожидание производной X' (t) = от случайной функции X (t) равно производной от ее математического ожидания:

m (t) =m’_x (t).

Доказательство. По определению производной,

Приравняем математические ожидания обеих частей равенства, а затем изменим порядок нахождения математического ожидания и предела (законность изменения порядка этих операций примем без доказательства):

Используя свойства математического ожидания,получим

Итак, m (t) =m’_x (t).

Замечание 1. По существу доказано, что для среднеквадратически дифференцируемых случайных функций операции нахождения математического ожидания и дифференцирования можно менять местами. Действительно, запишем доказанную теорему так:

М[Х' (t) ] ={М[Х (t) ]}'.

Мы видим, что в левой части равенства сначала находят производную, а затем математическое ожидание; в правой части—наоборот.

Пример 1. Зная математическое ожидание т_x (t) = ² +t случайной функции Х (t), найти математическое ожидание ее производной.

Решение. Искомое математическое ожидание

m (t) =m’_x (t) = [ t ² +t ]`=2 t +1.

Замечание 2. Если первая производная дифференцируема,топроизводную от первой производной называют второй производной и обозначают через X" (t). Аналогично определяют производные более высоких порядков.

Замечание 3. Теорему 1 можно обобщить: математическое ожидание производной порядка n равно производной этого же порядка от математического ожидания случайной функции.

Теорема 2. Корреляционная функция производной от случайной функции Х (t) равна второй смешанной производной от ее корреляционной функции:

.

Доказательство.По определению корреляционой функции,

Представим произведение производных как вторую смешанную частную производную:

Следовательно,

Изменив порядок операций нахождения математического ожидания и дифференцирования (на основании замечания 1), окончательно получим

 

Итак,

Пример 2. Зная корреляционную функцию K_x (t ₁, t ₂) = 2 t ₁ t ₂ +t ₁² t ₂² случайной функции Х (t), найти корреляционную функцию ее производной.

Решение. Найдем частную производную от заданной корреляционной функции по t ₁:

Найдем частную производную от полученного результата по t ₂:

Искомая корреляционная функция

Теорема 3. Взаимная корреляционная функция случайной функции Х (t) и ее производной X' (t) = равна частной производной от корреляционной функции по соответствующему аргументу [ если индекс при R записан на первом (втором) месте, то дифференцируют по первому (второму) аргументу ] :

a)

б)

Доказательство.

а) По определению взаимной корреляционной функции двух функций Х (t) и X' (t) = ,

Изменим порядок операций дифференцирования и нахождения математического ожидания:

Итак, искомая взаимная корреляционная функция

б) Доказывается аналогично.

| Пример 3. Задана корреляционная функция K_x (t ₁, t ₂) =t ₁ t ₂ e^{t 1 +t 2}случайной функции X (t). Найти взаимную корреляционную функцию

Решение. Воспользуемся формулой

Выполнив дифференцирование заданной корреляционной функции по t ₂, получим

Итак, искомая взаимная корреляционная функция