
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная случайного процесса и ее свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В соответствии с классическим определением, производная случайного процесса X(t) должна быть определена как предел разностного отношения
Случайный процесс X(t) называется дифференцируемым, если существует случайный процесс
При этом случайный процесс процесса X(t) и обозначается следующим образом:
Теорема 1. Математическое ожидание производной случайного процесса равно производной от математического ожидания самого слу- чайного процесса:
Следствие. Теорема 2. Корреляционная функция производной случайного процесса X(t) равна второй смешанной производной от его корреляционной функции:
Теорема 3. Взаимная корреляционная функция случайного процесса X(t) и его производной ционной функции по переменной, соответствующей производ- ной:
Интеграл от случайного процесса и его свойства Интегралом от случайного процесса X(t) на отрезке [0, t] называется предел в среднеквадратичном при λ→0 (n→0)
интегральных сумм где si Теорема 4. Математическое ожидание интеграла от случайного процесса равно интегралу от его математического ожидания:
Теорема 5. Корреляционная функция интеграла от случайного процесса X(t) равна двойному интегралу от его корреляционной функции:
Теорема 6. Взаимная корреляционная функция случайного процесса X(t) и его интеграла равна интегралу от корреляционной функции случайного процесса X(t):
Пример 6. Случайный процесс X(t) имеет вид: X(t)=Ae-t (t≥0), где А - произвольно распределенная непрерывная случайная величина, имеющая конечное математическое ожидание m и конечную дисперсию Решение. 1) Математическое ожидание, дисперсия, стандартное отклонение, корреляционная функция и нормированная корреляционная функция случайного процесса X(t) имеют вид (см. Пример 3):
2) Переходим к расчету характеристик случайного процесса
За исключением математического ожидания (которое поменяло знак), все остальные характеристики сохранились полностью. Взаимные корреляционные функции случайного процесса X(t) и его производной
3) В соответствии с Теоремами 41-64
Взаимные корреляционные функции случайного процесса X(t) и его интеграла Y(t):
Глава 4. Канонические разложения случайных процессов Понятие канонического разложения случайного процесса Случайная величина V называется центрированной, если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величины V на неслучайную функцию φφ(t): X(t)=V φ(t). Элементарный центрированный случайный процесс имеет следующие характеристики:
Выражение вида
где φik(t), k=1;2;…-неслучайные функции; Рассмотрим характеристики случайного процесса
Так как по условию
Очевидно, что один и тот же случайный процесс имеет различные виды канонического разложения в зависимости от выбора координатных функций. Более того, даже при состоявшемся выборе координатных функций существует произвол в распределении случайных величин Vк. На практике по итогам экспериментов получают оценки для математического ожидания и корреляционной функции:
получают значения дисперсий
Пример 7. Случайный процесс Х(t) имеет следующее каноническое разложение:
Решение. Из полученных ранее общих формул имеем:
В каждом сечении случайный процесс Х(t) имеет нормальное распределение, так как является линейной комбинацией некоррелированных нормально распределенных случайных величин Vk, при этом одномерная плотность распределения имеет вид:
Двумерный закон распределения также является нормальным и имеет следующую двумерную плотность распределения:
Пример 8. Известныо математическое ожидание mX(t) и корреляционная функция КX(t1;t2)=t1t2 случайного процесса Х(t), где
Решение. Корреляционная функция имеет следующее разложение
следовательно,
Так как то
Плотность распределения случайных величин Vk:
Каноническое разложение случайного процесса Х(t) имеет вид:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

 при h→0 в смысле соответствующей сходимости. Можно показать, что сходимость по вероятности обладает рядом недостатков, которые делают этот подход практически бесполезным.
при h→0 в смысле соответствующей сходимости. Можно показать, что сходимость по вероятности обладает рядом недостатков, которые делают этот подход практически бесполезным. X’(t) такой, что
X’(t) такой, что
 .
.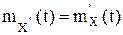 .
.  .
.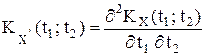 .
. X’(t) равна частной производной его корреля-
X’(t) равна частной производной его корреля- .
.

 ([ti; ti+1+1]); λ=max(ti+1 - ti), i=0,…,n-1.
([ti; ti+1+1]); λ=max(ti+1 - ti), i=0,…,n-1. ,
,  .
. .
.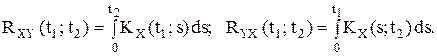
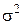 σ2. Найти характеристики случайных процессов X(t),
σ2. Найти характеристики случайных процессов X(t),  X’(t) и
X’(t) и 

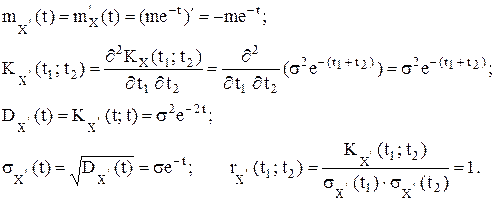

 основные характеристики интеграла от случайного процесса X(t) имеют следующие значения:
основные характеристики интеграла от случайного процесса X(t) имеют следующие значения:
 D (t1;t2)=?????????????
D (t1;t2)=?????????????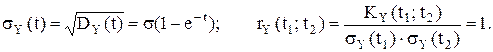


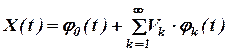 ,
,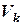 Vi, k=1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X(t), при этом случайные величины
Vi, k=1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X(t), при этом случайные величины 

 то
то
 . После разложения
. После разложения  в двойной ряд Фурье по координатным функциям φк(t):
в двойной ряд Фурье по координатным функциям φк(t):
 DVk случайных величин Vk.
DVk случайных величин Vk. , где Vk-нормально распределенные некоррелированные случайные величины с параметрами (0; σк); m0(t) - неслучайная функция. Найти основные характеристики случайного процесса Х(t), включая плотности распределения.
, где Vk-нормально распределенные некоррелированные случайные величины с параметрами (0; σк); m0(t) - неслучайная функция. Найти основные характеристики случайного процесса Х(t), включая плотности распределения.


 . Найти каноническое разложение Х(t) по координатным функциям
. Найти каноническое разложение Х(t) по координатным функциям  при условии, что коэффициенты разложения Vk - нормально распределенные случайные величины.
при условии, что коэффициенты разложения Vk - нормально распределенные случайные величины. ,
,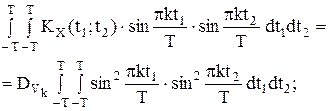 ;
; ;
; ;
; ,
, ;
;  .
.
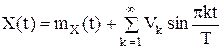 .
.


