
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Агрегат как случайный процессСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Если процесс функционирования реальной сложной системы по своему существу носит характер случайного процесса, для агрегата как математической модели системы используются основные понятия теории случайных процессов. Случайный процесс, протекающий в любой физической системе, представляет собой случайные переходы системы из состояния в состояние. Состояние системы может быть охарактеризовано с помощью численных переменных: в простейшем случае – одной, в более сложных – несколькими. Понятие случайного процесса представляет собой обобщение понятия случайной величины. Случайным процессом Таким образом, можно подвести итог. Существует большое количество форм агрегирования, т.е. объединения частей в целое. Их общность состоит в том, что агрегирование диктуется выбранной моделью описываемой системы. Агрегирование есть установление отношений между агрегируемыми элементами. Наиболее важными видами агрегатов являются агрегаты-структуры, агрегаты-операторы, агрегаты-статистики и случайные процессы. Метод наименьших квадратов Зависимость между случайными величинами полностью определяется совместной функцией распределения. Для системы двух случайных величин совместная функция распределения имеет вид: F(x,y). Восстановление совместных функций распределения в практических задачах весьма затруднительно. Поэтому на практике пользуются условными средними my и условными дисперсиями sy2. Зависимость дисперсии sy2 от параметра x называется скедастической зависимостью. В реальных практических задачах этой зависимостью пользуются редко. Как было отмечено в начале главы, зависимость условного среднего my от x называется регрессией. Запишем зависимость функции отклика y от фактора x в виде функции следующего вида: y=j(x)+e, M(e) = 0. Функция j(x) называется функцией регрессии случайной величины Y от X, а график этой функции – кривой регрессии Y на X. Для описания того, каким образом функцию j(x) можно оценить по имеющимся парам наблюдений (xi, yi) рассмотрим случай, когда j(x) = Модель в этом случае имеет вид: yi = Такая модель называется одномерной линейной регрессией. Восстановить модель, значит, определить ее коэффициенты. Для решения этой задачи будем применять метод наименьших квадратов. Рассмотрим функцию Устремим ее к минимуму. Необходимым условием минимума является равенство нулю первых частных производных данной функции по неизвестным параметрам
После элементарных преобразований получаем
Решая данную систему уравнений, получаем
Разделив в последнем выражении числитель и знаменатель на n, получим следующее выражение для оценки коэффициента b1:
Коэффициент Итак, продемонстрирован способ определения коэффициентов уравнения регрессии в случае одного фактора. Если количество факторов больше одного, процедура оценки аналогичная. Необходимо составлять функцию квадрата отклонения зафиксированных откликов от модели регрессии, определять первые частные производные по оцениваемым параметрам, приравнивать эти производные нулю и решать систему уравнений относительно этих параметров.
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 называется процесс, значение которого при любом фиксированном
называется процесс, значение которого при любом фиксированном  является случайной величиной
является случайной величиной  . Случайная величина
. Случайная величина  , в которую обращается случайный процесс при
, в которую обращается случайный процесс при  , называется сечением случайного процесса, соответствующим данному значению аргумента
, называется сечением случайного процесса, соответствующим данному значению аргумента  . Теория случайных процессов бурно развивается в настоящее время. Ее аппарат изложен в обширной литературе. Имеются частные случаи случайных процессов: марковские, полумарковские, винеровские, кусочно-непрерывные и т.п.
. Теория случайных процессов бурно развивается в настоящее время. Ее аппарат изложен в обширной литературе. Имеются частные случаи случайных процессов: марковские, полумарковские, винеровские, кусочно-непрерывные и т.п. 0 +
0 +  .
. ,
, .
. ,
, .
. 
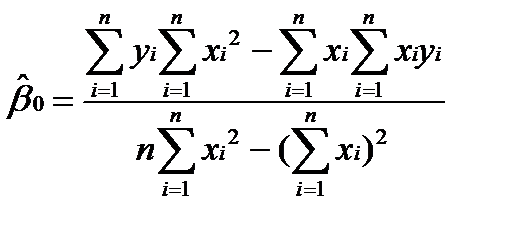 ,
,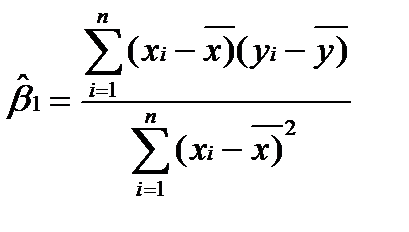 .
.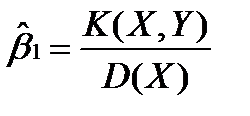 .
. можно найти проще по известному
можно найти проще по известному  , если воспользоваться первым уравнением системы:
, если воспользоваться первым уравнением системы:  .
.


