
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение значимости факторовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
При построении регрессионной модели встает вопрос определения значимости факторов, входящих в уравнение регрессии (1). Определение значимости фактора означает выяснение вопроса о силе влияния фактора на функцию отклика. Если в ходе решения задачи о проверке значимости фактора выясняется, что фактор незначим, то его можно исключить из уравнения. В этом случае считают, что фактор не оказывает существенного влияния на функцию отклика. Если же подтверждается значимость фактора, то его оставляют в модели регрессии. Считается, что в этом случае фактор оказывает влияние на функцию отклика, которым нельзя пренебрегать. Решение вопроса о значимости факторов эквивалентно проверке гипотезы о равенстве нулю коэффициентов регрессии при данных факторах. Таким образом, нулевая гипотеза будет иметь вид: Y = Xb+e,(2) Y – вектор размера n; X - матрица размера (p*n); b - вектор размера p. Уравнение (2) можно переписать в виде:
где X l и X p-l - матрицы размера (n,l) и (n,p-l) соответственно. Тогда гипотеза H0 эквивалентна предположению, что
Определим минимум функции
тогда как при H1 он равен
Для проверки нулевой гипотезы рассчитаем статистику Проверку значимости факторов можно проводить и другим методом, независимо друг от друга. Данный метод основан на исследовании доверительных интервалов для коэффициентов уравнения регрессии. Определим дисперсии коэффициентов
Таким образом, рассмотрена задача проверки значимости факторов и сокращения размерности модели в случае несущественного влияния факторов на функцию отклика. Далее здесь было бы логично рассмотреть вопрос о введении в модель дополнительных факторов, которые, по мнению исследователя, в ходе проведения эксперимента не были учтены, но их воздействие на функцию отклика существенно. Предположим, что уже после того, как подобрана модель регрессии
возникла задача включить в модель дополнительные факторы xj, чтобы модель с введением этих факторов приняла вид:
где X - матрица размера n*p ранга p, Z – матрица размера n*g ранга g и столбцы матрицы Z линейно не зависят от столбцов матрицы X, т.е. матрица W размера n*(p+g) имеет ранг (p+g). В выражении (3) использованы обозначения (X,Z)=W,
Во-вторых, можно уменьшить количество необходимых выкладок, используя те вычисления, которые были проведены в процессе подбора модели. Оценки коэффициентов нового уравнения регрессии можно рассчитать на основе формул:
где Таким образом, рассмотрены вопросы построения модели, позволяющие обоснованно выбирать состав факторов, включаемых в модель. Рассмотренные методы позволяют выводить из модели факторы, не оказывающие существенного влияния на функцию отклика и, с другой стороны, дополнять модель новыми факторами после того, как проведена серия опытов и проведены расчеты коэффициентов уравнения регрессии.
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 2369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.107 (0.01 с.) |

 , где
, где  подвектор вектора
подвектор вектора  размерности (l*1). Перепишем уравнение регрессии в матричном виде:
размерности (l*1). Перепишем уравнение регрессии в матричном виде:
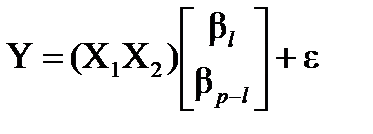 ,
, .
.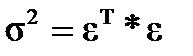 . Так как при соответствующих гипотезах H0 и H1 = 1- H0 оцениваются все параметры некоторой линейной модели, то минимум
. Так как при соответствующих гипотезах H0 и H1 = 1- H0 оцениваются все параметры некоторой линейной модели, то минимум  при гипотезе H0 равен
при гипотезе H0 равен ,
, .
. , которая имеет распределение Фишера с (l,n-p) степенями свободы, и критическая область для H0 образована 100*a процентами наибольших значений величины F. Если F<Fкр - гипотеза принимается, если F>Fкр - гипотеза отвергается.
, которая имеет распределение Фишера с (l,n-p) степенями свободы, и критическая область для H0 образована 100*a процентами наибольших значений величины F. Если F<Fкр - гипотеза принимается, если F>Fкр - гипотеза отвергается. ,
,  Значения
Значения  являются диагональными элементами матрицы
являются диагональными элементами матрицы  . Определив оценки дисперсий коэффициентов, можно построить доверительные интервалы для оценок коэффициентов уравнения регрессии. Доверительный интервал для каждой оценки
. Определив оценки дисперсий коэффициентов, можно построить доверительные интервалы для оценок коэффициентов уравнения регрессии. Доверительный интервал для каждой оценки 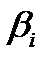 будет равен
будет равен  , где
, где  - табличное значение критерия Стьюдента при числе степеней свободы, с которым определялся элемент
- табличное значение критерия Стьюдента при числе степеней свободы, с которым определялся элемент  . Фактор с номером i значим, если абсолютная величина коэффициента при данном факторе больше величины отклонения, рассчитанного при построении доверительного интервала. Другими словами, фактор с номером i значим, если 0 не будет принадлежать доверительному интервалу, построенному для данной оценки коэффициента
. Фактор с номером i значим, если абсолютная величина коэффициента при данном факторе больше величины отклонения, рассчитанного при построении доверительного интервала. Другими словами, фактор с номером i значим, если 0 не будет принадлежать доверительному интервалу, построенному для данной оценки коэффициента  . На практике, чем уже доверительный интервал при заданном уровне значимости, тем с большей уверенностью можно говорить о значимости фактора. Для проверки значимости фактора по критерию Стьюдента можно воспользоваться формулой
. На практике, чем уже доверительный интервал при заданном уровне значимости, тем с большей уверенностью можно говорить о значимости фактора. Для проверки значимости фактора по критерию Стьюдента можно воспользоваться формулой  . Вычисленное значение t-критерия сравнивается с табличным при заданном уровне значимости
. Вычисленное значение t-критерия сравнивается с табличным при заданном уровне значимости 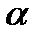 и соответствующем числе степеней свободы. Данным методом проверки значимости факторов можно пользоваться лишь в случае независимости факторов. Если есть основания считать ряд факторов зависимыми друг от друга, то данный метод может использоваться только для ранжирования факторов по степени их влияния на функцию отклика. Проверку значимости в этой ситуации необходимо дополнять методом, основанным на критерии Фишера.
и соответствующем числе степеней свободы. Данным методом проверки значимости факторов можно пользоваться лишь в случае независимости факторов. Если есть основания считать ряд факторов зависимыми друг от друга, то данный метод может использоваться только для ранжирования факторов по степени их влияния на функцию отклика. Проверку значимости в этой ситуации необходимо дополнять методом, основанным на критерии Фишера. ,
,  ,
, , (3)
, (3)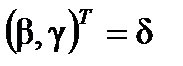 . Имеется две возможности определения оценок вновь введенных коэффициентов модели. Во-первых, можно найти оценку
. Имеется две возможности определения оценок вновь введенных коэффициентов модели. Во-первых, можно найти оценку  и ее дисперсионную матрицу непосредственно из соотношений
и ее дисперсионную матрицу непосредственно из соотношений .
.
 .
.


