
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1. Идентификация агрегатов.Содержание книги
Поиск на нашем сайте
Лабораторная работа 1. ИДЕНТИФИКАЦИЯ АГРЕГАТОВ.
Агрегаты-структуры Важной формой агрегирования является образование структур. Как и любой вид агрегата, структура является моделью системы и определяется совокупностью: объект, цель и средства моделирования. В результате получается многообразие типов структур: сетевые, древовидные, матричные. При синтезе создается структура будущей системы. Если это реальная система, то в ней установятся не только те связи, которые заложены в ходе проектирования, но и те, которые возникают из самой природы сводимых в систему элементов. Вспомним пример с подсистемами системы управления и защиты энергоблока АС. Функциональное дублирование возникает ввиду наличия соответствующих физических процессов, происходящих в установке, существует объективно, получается само собой. Далее, говоря об агрегатах-структурах, следует отметить, что при проектировании системы важно задать ее структуру во всех существенных отношениях. Рассмотрим пример, иллюстрирующий данный тезис. При проектировании радиотехнических приборов требуется разработка нескольких видов структур, а именно, блок-схема, принципиальная и монтажная схемы. Блок-схема определяется выпускаемыми промышленностью радиоэлементами, и прибор, в целом, делится на такие элементы. Принципиальная схема предполагает совершенно иное деление, т. к. она должна объяснять функционирование этого прибора. На ней выделены функциональные единицы - конденсаторы, диоды, транзисторы, которые могут не иметь пространственно локализованных аналогов, т.е. в реальности они выполнены в виде интегральных схем. Далее монтажная схема является результатом представления пространственной геометрии прибора, в пределах которого производится его монтаж. Таким образом, проект любой системы должен содержать разработку стольких структур, на скольких языках эта система описывается. Например, в организационных системах можно выделить иерархическую структуру подчиненности, структуру циркуляции информации, структуру производственного процесса и т.д. Эти структуры могут существенно отличаться топологически, но все они описывают с разных сторон одну и ту же систему и поэтому не могут быть не связаны между собой. Агрегаты-операторы Тип агрегата-оператора имеет место тогда, когда агрегируемые признаки фиксируются в числовых шкалах. В этом случае задается отношение на множестве признаков в виде числовой функции многих переменных, которая и является агрегатом. Основное применение агрегаты-операторы находят при описании динамических свойств системы. Представление зависимости выходных показателей системы в виде функционала от входных переменных есть пример агрегата-оператора. Рассмотрим формализованное определение агрегата-оператора. Пусть Рассмотрим оператор переходов
Аналогично оператор выходов однозначно определяет значения выходных характеристик системы и выражается следующим образом:
Если для системы удается представить зависимость ее выходных и входных параметров, управляющие воздействия и состояния в виде агрегата-оператора, то получается довольно хорошо формализованная математическая модель. Ограничивающим фактором для решения такого рода моделей, как правило, является только лишь большая размерность входящих в нее параметров.
Агрегаты-статистики Процессы функционирования реальных сложных систем во многих случаях носят случайный характер. Выходные характеристики таких систем принимают случайные значения из множества величин, описываемых некоторой функцией распределения Стохастические модели, в основе которых лежат предположения о законе распределения исследуемой случайной величины так же, как и агрегаты-операторы хорошо изучены. Имеется соответствующий математический аппарат, в современных операционных системах представлено обширное прикладное программное обеспечение, позволяющее успешно работать с подобного рода моделями. Метод наименьших квадратов Зависимость между случайными величинами полностью определяется совместной функцией распределения. Для системы двух случайных величин совместная функция распределения имеет вид: F(x,y). Восстановление совместных функций распределения в практических задачах весьма затруднительно. Поэтому на практике пользуются условными средними my и условными дисперсиями sy2. Зависимость дисперсии sy2 от параметра x называется скедастической зависимостью. В реальных практических задачах этой зависимостью пользуются редко. Как было отмечено в начале главы, зависимость условного среднего my от x называется регрессией. Запишем зависимость функции отклика y от фактора x в виде функции следующего вида: y=j(x)+e, M(e) = 0. Функция j(x) называется функцией регрессии случайной величины Y от X, а график этой функции – кривой регрессии Y на X. Для описания того, каким образом функцию j(x) можно оценить по имеющимся парам наблюдений (xi, yi) рассмотрим случай, когда j(x) = Модель в этом случае имеет вид: yi = Такая модель называется одномерной линейной регрессией. Восстановить модель, значит, определить ее коэффициенты. Для решения этой задачи будем применять метод наименьших квадратов. Рассмотрим функцию Устремим ее к минимуму. Необходимым условием минимума является равенство нулю первых частных производных данной функции по неизвестным параметрам
После элементарных преобразований получаем
Решая данную систему уравнений, получаем
Разделив в последнем выражении числитель и знаменатель на n, получим следующее выражение для оценки коэффициента b1:
Коэффициент Итак, продемонстрирован способ определения коэффициентов уравнения регрессии в случае одного фактора. Если количество факторов больше одного, процедура оценки аналогичная. Необходимо составлять функцию квадрата отклонения зафиксированных откликов от модели регрессии, определять первые частные производные по оцениваемым параметрам, приравнивать эти производные нулю и решать систему уравнений относительно этих параметров. Задание по лабораторной работе №1.
На вход агрегата (рисунок 1) поступают физические величины
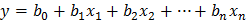 . .
Рисунок 1. Агрегат с входами и выходом Распределение входных величин известно (задано таблицей 2).
На основании заданного закона распределения случайного входа смоделировать по одному значению каждой величины xi1, i =1, n. Используя регрессионную зависимость, найти значение выхода y1. Повторить процедуру k раз. Заполнить таблицу 1
Таблица 1
Методом наименьших квадратов восстановить оператор выхода. Таблица 2. Распределение входных величин
Задание по лабораторной работе№2 На основании результатов моделирования, проведенного при выполнении предыдущей работы провести анализ качества построенной регрессионной модели, а именно: провести интервальное оценивание выходной характеристики, рассчитать значимость параметров модели, и провести проверку адекватности модели. Задание по лабораторной работе №3. На основании полученных ранее результатов провести расчеты нижнего и верхнего значений выходного показателя анализируемого агрегата. Провести анализ чувствительности. Лабораторная работа 1. ИДЕНТИФИКАЦИЯ АГРЕГАТОВ.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.15.22 (0.011 с.) |

 - множество моментов времени,
- множество моментов времени,  - множество входных сигналов,
- множество входных сигналов, 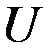 - множество сигналов управления,
- множество сигналов управления, 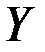 - множество выходных сигналов,
- множество выходных сигналов, 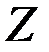 - множество состояний системы. Элементы указанных множеств назовем
- множество состояний системы. Элементы указанных множеств назовем  - моментом времени,
- моментом времени,  - входным сигналом,
- входным сигналом, 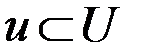 - управляющим сигналом,
- управляющим сигналом,  - выходным сигналом,
- выходным сигналом,  - состоянием системы. Все перечисленные сигналы будем рассматривать как функции времени
- состоянием системы. Все перечисленные сигналы будем рассматривать как функции времени  . Под агрегатом-оператором будем понимать объект, определяемый множествами
. Под агрегатом-оператором будем понимать объект, определяемый множествами 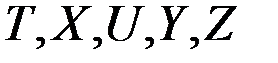 и операторами
и операторами 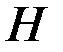 и
и  , которые являются оператором переходов
, которые являются оператором переходов 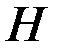 и оператором выходов
и оператором выходов  и
и 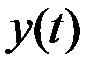 .
.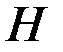 . Пусть даны состояния системы в моменты времени
. Пусть даны состояния системы в моменты времени  и
и 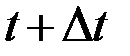 , т.е. предполагается, что система за время
, т.е. предполагается, что система за время  переходит из состояния
переходит из состояния  в состояние
в состояние 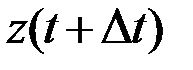 . Если известно, что в момент времени
. Если известно, что в момент времени 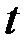 в систему поступают входные сигналы
в систему поступают входные сигналы 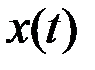 и управление
и управление 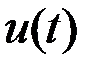 , то оператор переходов однозначно определяет состояние системы в следующий момент времени
, то оператор переходов однозначно определяет состояние системы в следующий момент времени  :
: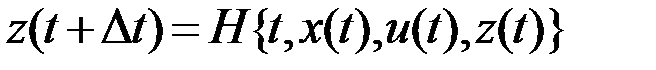 .
.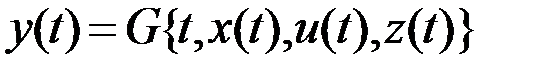 .
. , где
, где 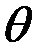 - вектор параметров закона распределения,
- вектор параметров закона распределения, 
 - некоторый момент времени. Если элементы вектора параметров функции распределения выражаются через достаточные статистики, тогда нет необходимости хранить всю информацию о реализованных характеристиках системы. Эту информацию можно заменить оценками параметров, полученными по реализовавшимся результатам наблюдений. Достаточные статистики - это агрегаты, которые извлекают всю полезную информацию об интересующем параметре из совокупности наблюдений. Примерами достаточных статистик являются параметры нормального закона распределения - математическое ожидание и дисперсия, параметр экспоненциального закона распределения -
- некоторый момент времени. Если элементы вектора параметров функции распределения выражаются через достаточные статистики, тогда нет необходимости хранить всю информацию о реализованных характеристиках системы. Эту информацию можно заменить оценками параметров, полученными по реализовавшимся результатам наблюдений. Достаточные статистики - это агрегаты, которые извлекают всю полезную информацию об интересующем параметре из совокупности наблюдений. Примерами достаточных статистик являются параметры нормального закона распределения - математическое ожидание и дисперсия, параметр экспоненциального закона распределения -  - характеристика. Использовать достаточные статистики необходимо с большой осторожностью. Их применение оправдано только в том случае, когда обоснован вид закона распределения, описывающий совокупность выходных величин. Дело в том, что агрегирование в данном случае является необратимым преобразованием, которое может привести к потере информации. Например, по сумме нельзя восстановить совокупность случайных величин слагаемых суммы.
- характеристика. Использовать достаточные статистики необходимо с большой осторожностью. Их применение оправдано только в том случае, когда обоснован вид закона распределения, описывающий совокупность выходных величин. Дело в том, что агрегирование в данном случае является необратимым преобразованием, которое может привести к потере информации. Например, по сумме нельзя восстановить совокупность случайных величин слагаемых суммы. 0 +
0 +  .
. ,
, .
. ,
, .
. 
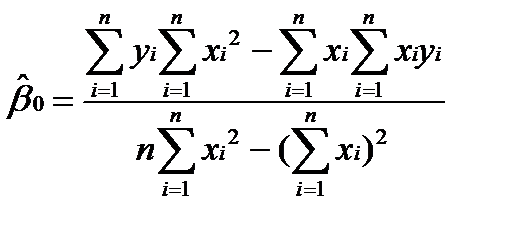 ,
,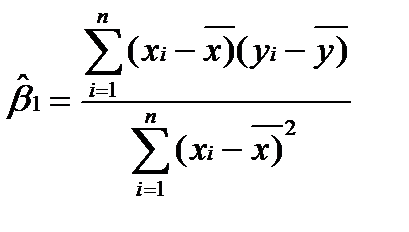 .
.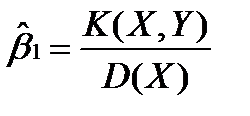 .
. можно найти проще по известному
можно найти проще по известному  , если воспользоваться первым уравнением системы:
, если воспользоваться первым уравнением системы:  .
. , имеющие случайную природу. На выходе наблюдается некоторая величина y, получающаяся в результате преобразования
, имеющие случайную природу. На выходе наблюдается некоторая величина y, получающаяся в результате преобразования 



