Обобщенный случай линейной регрессии

Обобщим рассмотренную задачу построения уравнения регрессии на случай, когда функция отклика зависит от множества факторов (x₁,x₂,…,x_k). Пусть Y – некоторая случайная величина, флуктуирующая вокруг некоторого неизвестного параметра h, т.е. y=h+e, где e - ошибка, y – отклик. Предположим, что h - можно представить в виде:

h = b₀ + b₁x₁ +…+ b_p-1x_p-1, (1)

где x₁, x₂,…, x_p-1 – факторы, которые в процессе опыта находятся под контролем экспериментатора и измеряются с пренебрежимо малой ошибкой, а b_j (j = 0,1,…,p-1) - неизвестные параметры, подлежащие оцениванию. Если значения x_j измеряются и при этом наблюдается n значений Y₁, Y₂,…, Y_n переменной y, то

Y_i = b₀ + b₁X _i1 +…+ b_p-1X _{i p-1} + e_i, ,

где X _ij представляет собой i-е значение фактора x_j. Запишем данное уравнение в матричной форме

= ,

или Y = Xb+e, X₁₀ = X₂₀ = … = X_n0 =1.

Матрица X размера n*p называется регрессионной матрицей, X – регрессоры, а Y – отклик.

Существенная черта моделей состоит в том, что они являются линейными по параметрам b_i. Оценку параметров производят методом наименьших квадратов, аналогично тому, как это было показано в случае однопараметрической модели. Необходимо минимизировать квадратичную ошибку. В матричном виде это

.

При получении данного выражения используется тот факт, что

.

Далее, дифференцируя ε^Тε по β и приравнивая результат нулю, получаем

или .

Откуда оценку для коэффициентов модели можно записать .

Если предположить, что ошибки являются несмещенными, т.е. , а факторы X неслучайными, то и есть несмещенная оценка вектора . Если, кроме того, предположить, что все ε_i некоррелированы и имеют одинаковую дисперсию и . Из данного выражения довольно просто получается следующая формула [8]:

Таким образом, получена оценка вектора параметров и формула для определения дисперсии данной оценки. Полученная оценка вектора параметров коэффициентов уравнения регрессии является оценкой наименьших квадратов, т.е. обладает наименьшей дисперсией.

 

Задание по лабораторной работе №1.

 

На вход агрегата (рисунок 1) поступают физические величины , имеющие случайную природу. На выходе наблюдается некоторая величина y, получающаяся в результате преобразования

Агрегат

x1

x2

…

xn

y

.

 

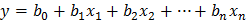Рисунок 1. Агрегат с входами и выходом

Распределение входных величин известно (задано таблицей 2).

 

На основании заданного закона распределения случайного входа смоделировать по одному значению каждой величины x_i1, i =1, n. Используя регрессионную зависимость, найти значение выхода y₁.

Повторить процедуру k раз.

Заполнить таблицу 1

 

 

Таблица 1

Номер опыта	x1	x2	…	xn	y
	x11	x21	…	xn1	y1
	x12	x22	…	xn2	y2
…	…	…	…	…	…
k	x1k	x2k		xnk	yk

 

Методом наименьших квадратов восстановить оператор выхода.

Таблица 2. Распределение входных величин

Вид закона распределения	Параметр 1	Параметр 2
Нормальное	M=(3-7)	Ϭ=(0.1-0.4)М
Равномерное	М-2 Ϭ	М+2 Ϭ
Экспоненциальное	1/М