Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория информационных процессовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ТЕОРИЯ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И СИСТЕМ
Модели информационных процессов
МОСКВА 2006 Разработано В.А. Мельником, канд. техн. наук. Под ред. О.И. Шелухина, д-ра техн. наук, проф., заслуженного деятеля науки РФ
КУРС: ТЕОРИЯ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И СИСТЕМ
Систематизированы основные сведения о типовых информационных процессах и их моделях, а также представлены основы моделирования информационных процессов.
ОГЛАВЛЕНИЕ Стр.
ДИДАКТИЧЕСКИЙ ПЛАН 5 ТЕМАТИЧЕСКИЙ ОБЗОР 7 1. ОСНОВЫ МОДЕЛИРОВАНИЯ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ 8 1.1. Системный подход к моделированию информационных процессов 8 1.1.1.Предмет теории моделирования 8 1.1.2.Роль и место моделирования в исследовании 9 информационных процессов и систем 9 1.1.3.Подходы к исследованию информационных процессов и систем 11 1.1.4.Классификация моделей 13 1.1.4.1.Физические модели 13 1.1.4.2.Математические модели 14 1.1.5.Моделирование систем и языки программирования 18 1.2. Математические схемы моделирования систем 21 1.2.1.Основные подходы к построению математических моделей информационных процессов и систем 21 1.2.1.1.Математические схемы 21 1.2.1.2.Типовые схемы 24 1.2.1.2.1.Непрерывно детерминированные модели (Д - схемы) 25 1.2.1.2.2.Дискретно – детерминированные модели (F-схемы) 26 1.2.1.2.3.Дискретно-стохастические модели (P-схемы) 31 1.2.1.2.4.Непрерывно-стохастические модели (Q - схемы) 32 1.2.1.2.5.Сетевые модели (N-схемы). Сети Петри 41 1.2.1.2.6.Обобщенные модели (А-схемы) 48 1.3. Организация и проведение вычислительного эксперимента 49 1.3.1. Методы планирования эксперимента на модели 49 1.3.2. Стратегическое планирование машинных экспериментов с моделями систем 53 1.3.3. Тактическое планирование машинных экспериментов с моделями систем 54 1.4. Планирование и реализация статистического моделирования информационных процессов на ЭВМ 56 1.4.1. Общая характеристика метода статистического моделирования 56 1.4.2. Псевдослучайные последовательности и процедуры их машинной генерации 57 1.4.3. Проверка и улучшение качества последовательностей псевдослучайных чисел 62 1.4.4. Моделирование случайных воздействий на системы 64 2. ТИПОВЫЕ ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ И ИХ МОДЕЛИ 70 2.1. Эталонная модель открытых систем 70 2.1.1. Основные элементы технологии открытых систем 2.1.1.1. Среда информационных технологий 2.1.1.2. Концепция открытых систем Ошибка! Закладка не определена. 2.1.2. Переносимость и способность к взаимодействию 2.1.3. Основные модели открытых систем и их развитие 2.1.3.1. Классификация моделей 2.1.3.2. Базовые стандартные модели 70 2.1.3.2.1. Модель ISO OSI 70 2.1.3.2.2. МодельPOSIXOSE 72 2.1.3.3. Модели сред открытых систем 74 2.1.3.4. Модели распределённых систем 75 2.2. Базовые информационные процессы и их классификация 80 2.2.1. Концептуальный уровень 81 2.2.2. Логический уровень 84 2.2.3. Физический уровень 87 2.3. Модели процесса передачи данных 89 2.4.1. Потери при информационном взаимодействии 93 2.4.2. Модель дискретного канала связи 99 2.4.3. Модель непрерыного канала связи 104 2.4.4. Информационный предел избыточности для канала с независимыми ошибками 106 2.4.5. Информационный предел избыточности для канала с пакетными ошибками 110 2.5. Модели процесса обработки данных 113 2.5.1. Модели обслуживания вычислительных задач 115 2.5.2. Модели планирования вычислительного процесса 124 2.5.3. Вычислительный граф системы обработки 128 2.6. Модели процесса хранения и накопления данных 130 2.6.1. Инфологическая модель предметной области 130 2.6.2. Информационный граф системы обработки 131 2.6.3. Каноническая структура информационной базы 136 2.6.4. Выбор ключевых реквизитов 139 2.7. Модели процесса формализации знаний 141 2.7.1. Логическая модель представления знаний 143 2.7.2. Алгоритмическая модель представления знаний 146 2.7.3. Семантическая модель представления знаний 148 2.7.4. Фреймовая модель представления знаний 150
ДИДАКТИЧЕСКИЙ ПЛАН Системный подход к моделированию информационных процессов. Методы моделирования информационных процессов и их характеристика. Математические схемы моделирования информационных процессов и систем. Организация и проведение вычислительного эксперимента. Планирование и реализация статистического моделирования информационных процессов на ЭВМ. Эталонная модель открытых систем и ее характеристика. Базовые информационные процессы и их классификация. Модели процесса доставки сообщений. Модели процесса хранения и накопления данных. Модели процесса обработки. Модели процесса формализации знаний. ЛИТЕРАТУРА
Основная *1.Болотова Л.С. Системы искусственного интеллекта: Теоретические основы интеллектуальных информационных систем и формальные модели представления знаний. Учебное пособие. – М.: МИРЭА (технический университет), 2003. *2.Душин В.К. Теоретические основы информационных процессов и систем. Учебник для вузов. – М.: Изд. торг. корп. «Дашков и К», 2003. *3.Острейковский В.А. Теория систем. Учебник для вузов. – М.: Высшая школа. 2003. *4. Шелухин О.И., Теняшев А.М., Осин А.В. Моделирование информационных систем. Учебное пособие. – М.: Сайнс-Пресс, 2005.
Дополнительная *1.Аскеров Т.М., Данчул А.Н., Бородько В.П., Гречишников А.В., Домрачеев А.В., Сафонова Т.Е. Информатика: Учебник. – М.: Изд-во РАГС, 2004. *2.Пранов Б.М. Проектирование АСОИУ: Учебное пособие. – М.: СГА, 2005. *3.Советов Б.Я. Информационная технология. Учебник для вузов. – М.: Высшая школа, 2005. *4.Советов Б.Я., Яковлев С.А. Моделирование систем. Учебник для вузов. – М.: Высшая школа, 2003. *5.Шастова Г.А. Выбор и автоматизация структуры информационных систем. – М.: Радио и связь, 1992.
Примечание. Знаком (*) отмечены работы, на основе которых составлен тематический обзор. ТЕМАТИЧЕСКИЙ ОБЗОР Информационная технология базируется на реализации информационных процессов, разнообразие которых требует выделения базовых, характерных для любой информационной технологии. К ним можно отнести управление, обмен, обработку, накопление данных и формализацию знаний. На логическом уровне должны быть построены математические модели, обеспечивающие объединение процессов в информационную технологию. Модель процесса передачи может быть представлена совокупностью моделей каналов связи и ошибок, являющихся следствием воздействия помех на передаваемые коды сообщений. Модель процесса обработки отображается моделью планирования и моделью реализации вычислений. В ходе обработки на основе входных данных формируются промежуточные и выходные, поэтому существенным становится процесс накопления, в основе которого должны лежать модели, обеспечивающие построение информационной базы. В условиях персонализации вычислений особую роль играют модели представления знаний. Распространение получили логическая, алгоритмическая, семантическая и фреймовая модели, а также их совместное использование. Выделение базовых информационных процессов и систем, характерных для любой информационной технологии определяют содержание данного учебного пособия. Умение моделировать информационные процессы и системы является залогом успешного изучения систем, принятия правильных решений при их проектировании. В данном учебном пособии рассматриваются базовые модели информационных процессов и систем, а также основы их моделирования, что позволит показать принципы их построения, сравнить варианты, дать рекомендации по выбору, а также выявить взаимосвязь информационных процессов и систем, их структурную соподчиненность. Материал данного учебного пособия базируется на теории вероятности и математической статистики, теории систем, теории графов.
ОСНОВЫ МОДЕЛИРОВАНИЯ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ
Системный подход к моделированию информационных процессов
Роль и место моделирования в исследовании Классификация моделей
Физические модели
В основу классификации положена степень абстрагирования модели от оригинала. Предварительно все модели можно подразделить на 2 группы — физические и абстрактные (математические). Физические модели обычно называют систему, эквивалентную или подобную оригиналу, но возможно имеющую другую физическую природу. В настоящее время выделяют следующие виды физических моделей: - натуральные; - квазинатуральные; - масштабные; - аналоговые. Натуральные модели — это реальные исследуемые системы (макеты, опытные образцы). Имеют полную адекватность (соответствия) с системой оригиналом, но дороги. Квазинатуральные модели — совокупность натуральных и математических моделей. Этот вид используется тогда, когда модель части системы не может быть математической из-за сложности её описания (модель человека оператора) или когда часть системы должна быть исследована во взаимодействии с другими частями, но их ещё не существует или их включение очень дорого (вычислительные полигоны, АСУ). Масштабная модель — это система той же физической природы, что и оригинал, но отличается от него масштабами. Методологической основой масштабного моделирования является теория подобия. При проектировании ВС масштабные модели могут использоваться для анализа вариантов компоновочных решений. Аналоговыми моделями называют системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрические системы. Аналоговое моделирование использует при исследовании средства ВТ на уровне логических элементов и электрических цепей, а так же на системном уровне, когда функционирование системы описывается, например, дифференциальными или алгебраическими уравнениями. Математические модели
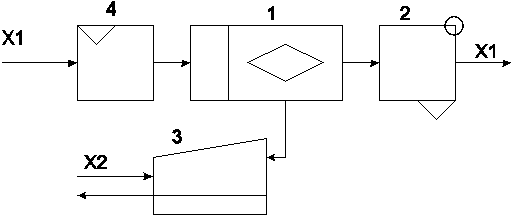
Математические модели представляют собой формализованное представление системы с помощью абстрактного языка, с помощью математических соотношений, отражающих процесс функционирования системы. Для составления математических моделей можно использовать любые математические средства — алгебраическое, дифференциальное, интегральное исчисления, теорию множеств, теорию алгоритмов и т.д. По существу вся математика создана для составления и исследования моделей объектов и процессов. К средствам абстрактного описания систем относятся также языки химических формул, схем, чертежей, карт, диаграмм и т.п. Выбор вида модели определяется особенностями изучаемой системы и целями моделирования, т.к. исследование модели позволяет получить ответы на определённую группу вопросов. Для получения другой информации может потребоваться модель другого вида. Математические модели можно классифицировать как детерминированные и вероятностные, аналитические, численные и имитационные. Детерминированное моделирование отображает процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, т. е. набор однородных реализаций. Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат. Численная модель характеризуется зависимостью такого вида, который допускает только частные решения для конкретных начальных условий и количественных параметров моделей. Имитационная модель — это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают возможности использования имеющихся математических методов аналитического и численного решения, но позволяют имитировать процесс функционирования системы и производить вычисления интересующих характеристик. Имитационные модели могут быть созданы для гораздо более широкого класса объектов и процессов, чем аналитические и численные. Поскольку для реализации имитационных моделей служат ИС, средствами формализованного описания ИМ служат универсальные и специальные алгоритмические языки. ИМ в наибольшей степени подходят для исследования ИС на системном уровне. Процедура имитационного моделирования. Метод ИМ заключается в создании логико-аналитической (математической модели системы и внешних воздействий), имитации функционирования системы, т.е. в определении временных изменений состояния системы под влиянием внешних воздействий и в поучении выборок значений выходных параметров, по которым определяются их основные вероятностные характеристики. Данное определение справедливо для стохастических систем. При исследовании детерминированных систем отпадает необходимость изучения выборок значений выходных параметров. Модель системы со структурным принципом управления представляет собой совокупность моделей элементов и их функциональные взаимосвязи. Модель элемента (агрегата, обслуживающего прибора) - это, в первую очередь, набор правил (алгоритмов) поведения устройства по отношению к выходным воздействиям (заявкам) и правил изменений состояний элемента. Элемент отображает функциональное устройство на том или ином уровне детализации. В простейшем случае устройство может находится в работоспособном состоянии или в состоянии отказа. В работоспособном состоянии устройство может быть занято, например, выполнение операции по обслуживанию заявки или быть свободным. К правилам поведения устройства относятся правила выборки заявок из очереди; реакция устройства на поступление заявки, когда устройство занято или к нему имеется очередь заявок; реакция устройства на возникновение отказа в процессе обслуживания заявки и некоторые другие. Т.о. имитационное моделирование (ИМ) — это метод исследования, который основан на том, что анализируемая динамическая система заменяется имитатором и с ним производятся эксперименты для получения об изучаемой системе. Роль имитатора зачастую выполняет программа ЭВМ. Основная идея метода ИМ состоит в следующем. Пусть необходимо определить функцию распределения случайной величины y. Допустим, что искомая величина y может быть представлена в виде зависимости: y=f(a,b,....,w), где a,b,....,w случайные величины с известными функциями распределения. Для решения задач такого вида применяется следующий алгоритм: 1) по каждой из величин a,b,....,w производится случайное испытание, в результате каждого определяется некоторое конкретное значение случайной величины ai,bi,....,wi; 2) используя найденные величины, определяется одно частное значение yi по выше приведённой зависимости; 3) предыдущие операции повторяются N раз, в результате чего определяется N значений случайной величины y; 4) на основании N значений величины находится её эмпирическая функция распределения. Имитация функционирования системы. Предположим, исследуется вычислительная система (ВС), состоящая из процессора 1 с основной памятью, устройство вода перфокарт 4, АЦПУ 2 и дисплея 3 (рис. 2.).
Рис. 2. Упрощённая схема моделируемой системы. Через устройство 4 поступает поток заданий Х1. Процессор обрабатывает задания и результаты выдаёт на АЦПУ 2. Одновременно с этим ВС используется, например, как информационно-справочная система. Оператор-пользователь, работающий за дисплеем, посылает в систему запросы Х2, которые обрабатываются процессором и ответы выводятся на экран дисплея. Процессор работает в 2-х программном режиме: в одном разделе обрабатываются задания Х1, в другом, с более высоким относительным приоритетом запросы Х2. Представим данную ВС в упрощённом варианте в виде стохастической сети из 4-х СМО. Потоки заданий и запросы будем называть потоками заявок. Считаем потоки Х1 и Х2 независимыми. Известны ф.р. периодов следования заявок t1 и t2 и длительность обслуживания Т1К , T2К заявок в к-ом устройстве. Требуется определить времена загрузки каждого устройства и времена реакции по каждому из потоков. Вначале определяется момент поступления в систему 1-ой заявки потока Х1 по результатам случайного испытания в соответствии с ф.р. периода следования заявок.
Рис. 3. Временная диаграмма функционирования ВС. На рис. 3 это момент времени t1=0+t11 (здесь и далее верхний индекс обозначает порядковый номер заявки данного потока). То же самое делается для потока Х2. На рис. 3 момент поступления 1-ой заявки потока Х2 t2=0+t21. Затем находится минимальное время, т.е. наиболее раннее событие. В примере это время t1. Для 1-ой заявки потока Х1определяется время обслуживания устройством ввода перфокарт Т114 методом случайного испытания и отмечается момент окончания обслуживания t4=t1+ Т114. На рис. показан переход устройства 4 в состояние «занято». Одновременно определяется момент поступления следующей заявки потока Х1: t12=t1+t12. Следующее минимальное время это момент поступления заявки потока Х2 - t2. Для этой заявки находится время обслуживания на дисплее Т123 и отслеживается время окончания обслуживания t3=t2+ Т123. Определяется момент поступления второй заявки потока Х2: t7=t2+t22. Снова выбирается минимальное время — это t3. В этот момент заявка потока Х2 начинает обрабатываться процессором. По результату случайного испытания определяется время её обслуживания T121 и отмечается момент t5=t3+ T121 окончания обслуживания. Следующее минимальное время t4 - момент завершения обслуживания заявки потока Х1 устройством 4. С этого момента заявка может начать обрабатываться процессором, но он занят обслуживанием потока Х2. Тогда заявка потока Х1 переходит в состояние ожидания, становиться в очередь. В следующий момент времени t5 освобождается процессор. С этого момента процессор начинает обрабатывать заявку потока Х1, а заявка потока Х2 переходит на обслуживание дисплеем, т.е. ответ на запрос пользователя передаётся из основной памяти в буферный накопитель дисплея. Далее определяются соответствующие времена обслуживания: T111 и T123 и отмечаются моменты времени t9=t5+ T111 и t6=t5+ T123. В момент t6 полностью завершается обработка первой заявки потока Х2. По разности времени t6 и t2 вычисляется время реакции по этой заявке u12= t6- t2. Следующий минимальный момент t7 - это наступление 2-ой заявки потока Х2. Определяет время поступления очередной заявки этого потока t15= t7+t23. Затем вычисляется время обслуживания 2-ой заявки на дисплее T223 и отмечается момент t8=t7+ T223, после чего заявка становится в очередь, т.к. процессор занят. Эта заявка поступит на обслуживание в процессор только после его освобождения в момент t9. В этот момент заявка потока Х1 начинает обслуживаться в АЦПУ. Определяются времена обслуживания Т221 и Т112 по результатам случайных испытаний и отмечаются моменты окончания обслуживания t11= t9+Т223 и t10= t9+Т112. В момент времени t10 завершается полное обслуживание 1-ой заявки потока Х1. Разность между этим моментом и моментом времени t1 даёт 1-ое значение времени реакции по потоку Х1 u11= t10- t1. Указанные процедуры выполняются до истечения времени моделирования. В результате получается некоторое количество (выборка) случайных значений времени реакции (u1) и (u2) по 1-ому и 2-ому потокам. По этим значениям могут быть определены эмпирические функции распределения и вычислены количественные вероятностные характеристики времени реакции. В процессе моделирования можно суммировать продолжительности занятости каждого устройства обслуживанием всех потоков. Например, на рис. 3 занятость процессора 1 выделена заштрихованными ступеньками. Если результаты суммирования разделить на время моделирования, то получатся коэффициенты загрузки устройств. Можно определить время ожидания заявок в очереди, обслуженных системой, среднюю и максимальную длину очереди заявок к каждому устройству, требуемая ёмкость памяти и др. Имитация даёт возможность учесть надёжностные характеристики ВС. В частности, если известны времена наработки на отказ и восстановления всех входящих в систему устройств, то определяются моменты возникновения отказов устройств в период моделирования и моменты восстановления. Если устройство отказало, то возможны решения: - снятие заявки без возврата; - помещение заявки в очередь и дообслуживание после восстановления; - поступление на повторное обслуживание из очереди.
Математические схемы
Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования. Например, представление процесса функционирования информационно-вычислительной системы коллективного пользования в виде сети схем массового обслуживания дает возможность хорошо описать процессы, происходящие в системе, но при сложных законах распределения входящих потоков и потоков обслуживания не дает возможности получения результатов в явном виде. Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель – математическая схема – математическая [аналитическая или (и) имитационная] модель». Каждая конкретная система S характеризуется набором свойств, под которыми понимаются величины, отражающие поведение моделируемого объекта (реальной системы) и учитывающие условия ее функционирования во взаимодействии с внешней средой (системой) Е. При построении математической модели системы необходимо решить вопрос об ее полноте. Полнота модели регулируется в основном выбором границы «система S – среда Е». Также должна быть решена задача упрощения модели, которая помогает выделить основные свойства системы, отбросив второстепенные. Причем отнесение свойств системы к основным или второстепенным существенно зависит от цели моделирования системы (например, анализ вероятностно-временных характеристик процесса функционирования системы, синтез структуры системы и т. д.). ММ объекта моделирования, т.е. системы S можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества: - совокупность Х - входных воздействий на S хiÎХ, i=1…nx; - совокупность воздействий внешней среды vlÎV, l=1…nv; - совокупность внутренних (собственных) параметров системы hkÎH, k=1…nh; - совокупность выходных характеристик системы yjÎY, j=1…ny. В перечисленных множествах можно выделить управляемые и неуправляемые величины. В общем случае X, V, H, Y не пересекаемые множества, содержат как детерминированные так и стохастические составляющие. Входные воздействия Е и внутренние параметры S являются независимыми (экзогенными) переменными,
где Алгоритм функционирования AS — метод получения выходных характеристик Соотношение (1) является математическим описанием поведения объекта S моделирования во времени t, т.е. отражает его динамические свойства. Выражение для Для статических условий ММ есть отображения X, V, H в Y, т.е.
Соотношения для Также соотношения в ряде случаев могут быть получены через свойства системы в конкретные моменты времени, называемые состояниями. Состояния системы S характеризуются векторами:
где Z1(t), Z2(t)… Zk(t) - это координаты точки в к-мерном фазовом пространстве. Каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний Состояние системы S в интервале времени t0<t£Tl полностью определяется начальными условиями
иначе:
Время в модели S может рассматриваться на интервале моделирования (t0, T) как непрерывное, так и дискретное, т.е. квантованное на отрезке длины Dt. Таким образом под ММ объекта понимаем конечное множество переменных { Моделирование называется детерминированным, если операторы F, Ф детерминированные, т.е. для конкретного входа выход детерминированный. Детерминированное моделирование - частный случай стохастического моделирования. В практике моделирование объектов в области системного анализа на первичных этапах исследования рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания (СМО) и т.д. Не обладая такой степенью общности, как векторные модели, типовые математические схемы имеют преимущество простоты и наглядности, но при существенном сужении возможности применения. В качестве детерминированных моделей, когда при исследовании случайный факт не учитывается, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные и др. уравнения, а для представления систем, функционирующих в дискретном времени — конечные автоматы и конечно разностные схемы. В начале стохастических моделей (при учёте случайного фактора) для представления систем с дискретным временем используются вероятностные автоматы, а для представления систем с непрерывным временем — СМО. Большое практическое значение при исследовании сложных индивидуальных управленческих систем, к которым относятся ИС, имеют так называемые агрегативные модели. Aгрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивая взаимодействие частей.
Типовые схемы
Приведенные математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем. Однако в практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри и т.д. Не обладая такой степенью общности, как рассмотренные модели, типовые математические схемы имеют преимущества простоты и наглядности, но при существенном сужении возможностей применения. В качестве детерминированных моделей, когда при исследовании случайные факторы не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегро-дифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени, – конечные автоматы и конечно-разностные схемы. В качестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а для представления системы с непрерывным временем – системы массового обслуживания и т.д. Перечисленные типовые математические схемы, естественно, не могут претендовать на возможность описания на их базе всех процессов, происходящих в больших информационно-управляющих системах, к которым относятся ИС. Для таких систем в ряде случаев более перспективным является применение агрегативных моделей. Агрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект (система) расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей. Таким образом, при построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывно-детерминированный (например, дифференциальные уравнения); дискретно-детерминированный (конечные автоматы); дискретно-стохастический (вероятностные автоматы); непрерывно-стохастический (системы массового обслуживания); обобщенный, или универсальный (агрегативные системы). Математические схемы, рассматриваемые далее, должны помочь оперировать различными подходами в практической работе при моделировании конкретных систем.
Обобщенные модели (А-схемы) Обобщенный подход базируется на понятии агрегативной системы (от англ, aggregate system), представляющей собой формальную схему общего вида, которую будем называть А-схемой. Этот подход позволяет описывать поведение непрерывных и дискретных, детерминированных и стохастических систем Комплексное решение проблем, возникающих в процессе создания и машинной реализации модели, возможно лишь в случае, если моделирующие системы имеют в своей основе единую формальную математическую схему, т. е. А-схему. А-схема должна выполнять несколько функций: - являться адекватным математическим описанием объекта моделирования; - позволять в упрощенном варианте (для частных случаев) проводить аналитические исследования. Представленные требования несколько противоречивы, но в рамках обобщенного подхода на основе А-схем удается найти между ними компромисс. При агрегативном подходе первоначально дается формальное определение объекта моделирования — агрегативной системы. При агрегативном описании сложный объект (система) разбивается на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие их взаимодействие. В случае сложной организации полученных подсистем, подсистемы декомпозируются до уровней в которых они могут быть удобно математически описаны. В результате сложная система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, объединенных в подсистемы различных уровней. Элементом А-схемы является агрегат. Связь между агрегатами (внутри системы S и с внешней средой E) осуществляется с помощью оператора сопряжения R. Агрегат может рассматриваться как А-схема, т. е. может разбиваться на элементы (агрегаты) следующего уровня. Характеристиками агрегата являются множества моментов времени Т, входных X и выходных Y сигналов, состояний Z в каждый момент времени t. Пусть переход агрегата из состояния z(t1) в состояние В начальный момент времени t0 состояния z имеют значения, равные z°, т. е. z°=z(t0), которые задаются законом распределения L [z(t0)]. Пусть изменение состояния агрегата при входном сигнале хп описывается случайным оператором V. Тогда для момента времени
Если на интервале времени (tn, tn+i) нет поступления сигналов, то для
Так как на оператор U не накладываются ни какие ограничения, то допустимы скачки состояний dz в моменты времени, не являющимися моментами поступления входных сигналов x. Моменты скачков dz называются особыми моментами времени ts, состояния z(ts) — особыми состояниями А-схемы. Для описания скачков состояний dz в особые моменты времени ts используется случайный оператор W, которыйпредставляет собой частный случай оператора U | ||
|
| Поделиться: |

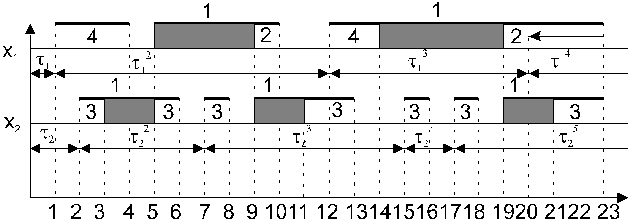
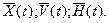 Выходные характеристики - зависимые переменные (эндогенные)
Выходные характеристики - зависимые переменные (эндогенные) 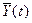 . Процесс функционирования S описывается оператором FS:
. Процесс функционирования S описывается оператором FS: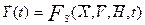
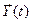 - выходная траектория; FS - закон функционирования S (FS может быть функция, функционал, логические условия, алгоритм, таблица или словесное описание правил).
- выходная траектория; FS - закон функционирования S (FS может быть функция, функционал, логические условия, алгоритм, таблица или словесное описание правил).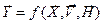
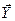 могут быть заданы формулами, таблицами и т.д.
могут быть заданы формулами, таблицами и т.д.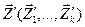 и
и 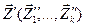 ,
,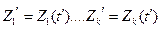 в момент
в момент 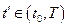 ;
; 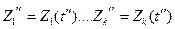 в момент
в момент 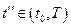 и т.д.
и т.д. 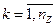 .
.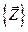 называется пространством состояний объекта моделирования Z, причём zkÎZ.
называется пространством состояний объекта моделирования Z, причём zkÎZ.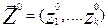 , где
, где 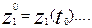 входными
входными 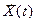 , внутренними параметрами
, внутренними параметрами 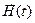 и воздействиями внешней среды
и воздействиями внешней среды 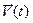 , которые имели место за промежуток времени t* - t0 c помощью 2-х векторных уравнений:
, которые имели место за промежуток времени t* - t0 c помощью 2-х векторных уравнений: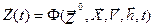 ;
;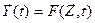 .
.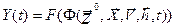 .
.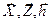 } вместе с математическими связями между ними и характеристиками
} вместе с математическими связями между ними и характеристиками 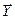 .
. происходит за малый интервал времени dz. Переходы из состояния z(t1) в z(t2) определяются внутренними параметрами агрегата
происходит за малый интервал времени dz. Переходы из состояния z(t1) в z(t2) определяются внутренними параметрами агрегата 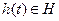 входными сигналами
входными сигналами 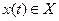 .
.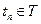 при поступлениивходного сигнала хn состояние определяется как
при поступлениивходного сигнала хn состояние определяется как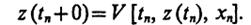
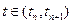 состояние агрегата определяется случайным оператором U, можно записать
состояние агрегата определяется случайным оператором U, можно записать