
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одноканальная СМО с отказами.Содержание книги
Поиск на нашем сайте
Дано: система имеет один канал обслуживания, на который поступает простейший поток заявок с интенсивностью Найти: абсолютную и относительную пропускную способность СМО и вероятность того, что заявка, пришедшая в момент времени t, получит отказ. Система при любом t > 0 может находиться в двух состояниях: S 0 – канал свободен; S 1 – канал занят. Переход из S 0 в S 1 связан с появлением заявки и немедленным началом ее обслуживания. Переход из S 1 в S 0 осуществляется, как только очередное обслуживание завершится (рис.9).
Рис.9. Граф состояний одноканальной СМО с отказами Выходные характеристики (характеристики эффективности) этой и других СМО будут даваться без выводов и доказательств. Абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени):
где Относительная пропускная способность (средняя доля заявок, обслуживаемых системой):
Вероятность отказа (вероятность того, что заявка покинет СМО необслуженной):
Очевидны следующие соотношения: N – канальная СМО с отказами (задача Эрланга). Это одна из первых задач теории массового обслуживания. Она возникла из практических нужд телефонии и была решена в начале 20 века датским математиком Эрлангом. Дано: в системе имеется n – каналов, на которые поступает поток заявок с интенсивностью Найти: абсолютную и относительную пропускную способность СМО; вероятность того, что заявка, пришедшая в момент времени t, получит отказ; среднее число заявок, обслуживаемых одновременно (или, другими словам, среднее число занятых каналов). Решение. Состояние системы S (СМО) нумеруется по максимальному числу заявок, находящихся в системе (оно совпадает с числом занятых каналов): · S 0 – в СМО нет ни одной заявки; · S 1 – в СМО находится одна заявка (один канал занят, остальные свободны); · S 2 – в СМО находится две заявки (два канала заняты, остальные свободны); ·... · S n – в СМО находится n – заявок (все n – каналов заняты). Граф состояний СМО представлен на рис. 10.
Рис.10. Граф состояний для n – канальной СМО с отказами Почему граф состояний размечен именно так? Из состояния S 0 в состояние S 1 систему переводит поток заявок с интенсивностью Почему такие интенсивности у нижних стрелок (дуг графа)? Пусть система находится в состоянии S 1 (работает один канал). Он производит Выходные характеристики (характеристики эффективности) данной СМО определяются следующим образом. Абсолютная пропускная способность:
где n – количество каналов СМО; Для того, чтобы написать формулу для определения
Рис.11. Граф состояний для схемы «гибели и размножения» Граф, представленный на этом рисунке, называют еще графом состояний для схемы «гибели и размножения». Напишем сначала для
Кстати, остальные финальные вероятности состояний СМО запишутся следующим образом. Вероятность того, что СМО находится в состоянии S 1, когда один канал занят:
Вероятность того, что СМО находится в состоянии S 2, т.е. когда два канала заняты:
Вероятность того, что СМО находится в состоянии S n, т.е. когда все каналы заняты.
Теперь для n – канальной СМО с отказами
При этом
Относительная пропускная способность:
Напомним, что это средняя доля заявок, обслуживаемых системой. При этом
Вероятность отказа:
Напомним, что это вероятность того, что заявка покинет СМО необслуженной. Очевидно, что Среднее число занятых каналов (среднее число заявок, обслуживаемых одновременно):
При этом
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.248.17 (0.006 с.) |

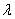 . Поток обслуживаний имеет интенсивность
. Поток обслуживаний имеет интенсивность 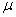 . Заявка, заставшая систему занятой, сразу же покидает ее.
. Заявка, заставшая систему занятой, сразу же покидает ее.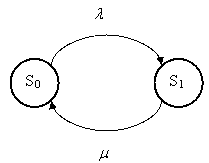
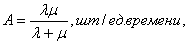
 );
);  ).
).
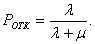
 и
и  .
.
 и т.д.
и т.д.
 – вероятность нахождения СМО в начальном состоянии, когда все каналы свободны (финальная вероятность нахождения СМО в состоянии S 0);
– вероятность нахождения СМО в начальном состоянии, когда все каналы свободны (финальная вероятность нахождения СМО в состоянии S 0);





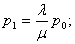



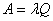 ;
;

 .
.


