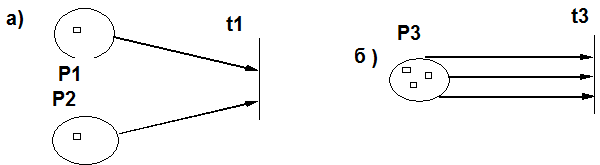Сетевые модели (N-схемы). Сети Петри

 

Теоретические основы сетей Петри: принципы построения, алгоритмы поведения. Сети Петри были разработаны и используются для моделирования систем, которые содержат взаимодействующие параллельные компоненты, например аппаратное и программное обеспечение ЭВМ, гибкие производственные системы, а также социальные и биологические системы. Впервые сети Петри предложил Карл Адам Петри в своей докторской диссертации «Связь автоматов» в 1962 году. Работа Петри привлекла внимание группы исследователей, работавших под руководством Дж. Денниса над проектом МАС в Массачусетском Технологическом институте. Эта группа стала источником значительных исследований и публикаций по сетям Петри. Полная оценка и понимание современной теории сетей Петри требуют хорошей подготовки в области математики, формальных языков и автоматов. Современный инженер - системотехник должен иметь квалификацию, необходимую для проведения исследований с помощью сетей Петри.

Сети Петри - инструмент исследования систем. Сети Петри делают возможным моделирование системы математическим представлением ее в виде сети Петри. Математическим аппаратом сетей Петри является теория комплектов. Теория комплектов представляет собой естественное расширение теории множеств. Как и множество, комплект является набором элементов из некоторой области. Однако в отличие от множества комплекты допускают наличие нескольких экземпляров одного и того же элемента. В отличие от множества, где элемент либо является элементом множества, либо нет, в комплект элемент может входить заданное число раз.

Пусть область представляет собой {a,b,c,d}, тогда комплекты над этой областью будут иметь вид:

B1={a,b,c} B2={a} B3={a,b,c,c}

B4={a,a,a} B5={b,c,b,c} B6={c,c,b,b}

B7={a,a,a,a,a,a,b,b,b,b,b,c,d,d,d,d,d}

Основным понятием теории комплектов является функция числа экземпляров. Обозначение #(x,B) число х в В т.е. число экземпляров элемента х в В. Если ограничить число элементов в комплекте так, что 0 <= #(x,B) <= 1, то получим теорию множеств.

Элемент х является членом комплекта В, если #(x,B) > 0. Аналогично, если #(x,B) = 0 то х не принадлежит В.

Определим пустой комплект 0, не имеющий членов (для всех х: #(x,0) = 0). Под мощностью |В| комплекта В понимается общее число экземпляров в комплекте |B| = S_x #(x,B).

Комплект А является подкомплектом комплекта В (обозначается АÍВ), если каждый элемент А является элементом В по крайней мере не больше число раз, т.е. АÍВ тогда и только тогда, когда #(x,A) <= #(x,B) для всех х.

Два комплекта равны (А = В), если #(x,A) = #(x,B).

Комплект А строго включен в комплект В (АÍВ), если АÍВ и А не равно В. Над комплектами определены 4 операции. Операции для двух комплектов А и В:

1. Объединение АÈВ: #(x,AÈB) = max (#(x,A),#(x,B));

2. Пересечение А ÇВ: #(x,A ÇB) = min (#(x,A),#(x,B));

3. Сумма А + В: #(x,A + B) = #(x,A)+#(x,B);

4. Разность А - В: #(x,A - B) = #(x,A) - #(x,B);

Назовем множество элементов, из которых составляются комплекты, областью D. Пространство комплектов Dⁿ есть множество всех таких комплектов, что элементы их принадлежат D и ни один из элементов не входит в комплект более n раз. Иначе говоря, для любого В Î Dⁿ:

а) из х Î В следует х Î D;

б) для любого х #(x,B) <= n.

Множество D^¥ есть множество всех комплектов над областью D, без какого либо ограничения на число экземпляров элемента в комплекте.

Сеть Петри состоит из 4 компонентов, которые и определяют ее структуру:

- множество позиций Р,

- множество переходов Т,

- входная функция I,

- выходная функция О.

Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход t_j в множество позиций I(t_j), называемых входными позициями перехода. Выходная функция О отображает переход t_j в множество позиций О(t_j), называемых выходными позициями перехода. Т.е.

(I: T -> P^¥)

(O: T -> P^¥).

Определение. Сеть Петри С является четверкой

С = (P,T,I,O)

где Р={p1,p2,...,p_n} конечное множество позиций, n>=0; T={t1,t2,...,t_m} конечное множество переходов, m>=0; I: T -> P^¥ является входной функцией - отображением из переходов в комплекты позиций; O: T -> P^¥ выходная функция - отображение из переходов в комплекты позиций. Множества позиций и переходов не пересекаются.

Мощность множества Р есть число n, а мощность множества Т есть число m. Произвольный элемент Р обозначается символом p_i, i=1...n; а произвольный элемент Т - символом t_j, j=1...m.

Позиция p_i является входной позицией перехода t_j, в том случае, если p_i Î I(t_j); p_i является выходной позицией перехода, если pi Î O(t_j).

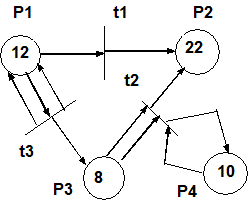
Входы и выходы переходов представляют комплекты позиций. Кратность входной позиции для перехода t_j есть число появлений позиции во входном комплекте перехода #(p_i,I(t_j)). Аналогично, кратность выходной позиции p_i для перехода t_j есть число появлений позиции в выходном комплекте перехода #(p_i,O(t_j)).

Определим, что переход t_j является входом позиции p_i, если p_i есть выход t_j (рис. 2). Переход t_j есть выход позиции p_i, если p_i есть вход t_j (рис. 1).

Определим расширенную входную функцию I и выходную функцию О таким образом, что #(t_j,I(p_i)) = #(p_i,O(t_j)); #(t_j,O(p_i)) = #(p_i,I(t_j)).

Для иллюстрации понятий теории сетей Петри гораздо более удобно графическое представление сети Петри. Теоретико - графовым представлением сети Петри является двудольный ориентированный мультиграф. В соответствии с этим граф сети Петри обладает двумя типами узлов:

кружок O является позицией,

планка | является переходом.

Ориентированные дуги соединяют позиции и переходы. Дуга направленная от позиции p_i к переходу t_j определяет позицию, которая является входом перехода t_j. Кратные входы в переход указываются кратными дугами из входных позиций в переход. Выданая позиция указывается дугой от перехода к позиции. Кратные входы также представлены кратными дугами.

Определение. Граф G сети Петри есть двудольный ориентированный мультиграф G=(V,A), где V = {v1,V2,...,v_s} - множество вершин; А = {a1,a2,...,a_r} - комплект направленных дуг, a_i={v_j,v_k}, где v_j,v_k Î V.

Множество V может быть разбито на 2 непересекающихся подмножества Р и Т, таких что P ÇT = 0, и если a_i = (v_j,v_k), тогда либо v_j Î P и v_k Î T, либо v_j ÎT и v_k Î P.

Сеть Петри есть мультиграф, т.к. он допускает существование кратных дуг от одной вершины к другой. Т.к. дуги направлены, то это ориентированный мультиграф. Граф является двудольным, т.к. он допускает существование вершин двух типов: позиций и переходов.

Маркировка m есть присвоение фишек позициям сети Петри. Фишка - это одна из компонент сети Петри (подобно позициям и переходам). Фишки присваиваются позициям. Их количество при выполнении сети может изменяться. Фишки используются для отображения динамики системы.

Маркированная сеть Петри есть совокупность структуры сети Петри C = (P,T,I,O) и маркировки m и может быть записана в виде M = (P,T,I,O, m). На графе сети Петри фишки изображаются крупными точками в кружке, который представляет позицию сети Петри. Количество фишек (точек) для каждой позиции не ограничено и, следовательно, в целом для сети существует бесконечно много маркировок. Множество всех маркировок сети, имеющей n позиций, является множеством всех n векторов, т.е. Nⁿ. Очевидно, что хотя это множество и бесконечно, но оно счетно. Когда маркировка превышает 4 или 5 фишек, то в кружках удобнее не рисовать фишки, а указывать их количество как на рис.15.

Рис. 15. Сеть Петри.

Маркировка m=(12,22,8,10) - как вектор. Может оказаться, что структура остается неизменной, а маркировка иная, например вектор маркировки будет иметь вид m = (13,22,9,10)

Выполнением сети Петри управляют количество и распределение фишек в сети. Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции.

Переход запускается, если он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число фишек по крайней мере равное числу дуг из позиции в переход. Фишки во входной позиции, которые разрешают переход, называются его разрешающими фишками. Например, если позиции р1 и р2 служат входами для перехода t1, тогда t1 разрешен, если р1 и р2 имеют хотя бы по одной фишке. Для перехода t3 с входным комплектом {p3,p3,p3} позиция р3 должна иметь не менее 3 фишек для разрешения перехода t3 (рис. 16).

 

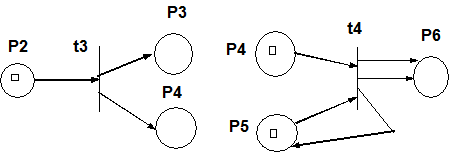
Рис. 16. Обозначение переходов в сетях Петри.

Определение. Переход t_j, Î Т маркированной сети Петри С = (Р,T,I,O,m) с маркировкой m, разрешен, если для всех p_i, Î P, m(p_i)>=#(p_i,I(t_j)).

Переход запускается удалением разрешающих фишек, из всех его выходных позиций (количество удаленных фишек для каждой позиции соответствует числу дуг, идущих из этой позиции в переход), с последующим помещением фишек в каждую из его выходных позиций (количество помещаемых фишек в позицию соответствует количеству дуг входящих в данную позицию из перехода).

Переход t3 I(t3) = {p2} и O(t3) = {p3,p4} разрешен каждый раз, когда в р2 будет хотя бы одна фишка. Переход t3 запускается удалением одной фишки из позиции р2 и помещением одной фишки в позицию р3 и р4 (его выходы). Переход t4, в котором I(t4) = {p4,p5} и O(t4) = {p5,p6,p6} запускается удалением по одной фишке из позиций р4 и р5, при этом одна фишка помещается в р5 и две в р6 (рис.17).

Рис. 17. Запуск переходов в сетях Петри.

Определение. Переход t_j в маркированной сети Петри с маркировкой m может быть запущен всякий раз, когда он разрешен. В результате запуска разрешенного перехода t_j образуется новая маркировка m': m'(p_i) = m (p_j)-#(p_i,I(t_j)+#(p_i,O(t_j)).