
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели обслуживания вычислительных задачСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При наличии плана организации вычислительного процесса основная проблема заключается в обслуживании заявки, которое характеризуется временем пребывания заявки в системе. Это время складывается из времени ожидания в очереди и времени обслуживания, представляющего собой время обработки информации процессором на основе принятой программы. Анализ процесса обслуживания заявки может быть выполнен на основе теории массового обслуживания. Тогда вычислительная система может быть представлена математической моделью системы массового обслуживания, которая характеризуется числом обслуживающих приборов, т. е. ЭВМ, дисциплиной образования очереди, числом вычислительных задач в ИВЗ, дисциплиной обслуживания очереди с помощью диспетчера Д2. В зависимости от того, какое число ЭВМ используется, различают одно- и многолинейные системы. Даже для многолинейной системы может наблюдаться случай, когда все обслуживающие приборы, т. е. ЭВМ, будут заняты. Тогда модель системы может предполагать такой поток заявок, который не ждет обслуживания, и возникает система с потерями. Физически это возможно либо когда очередь не предусматривается, либо когда имеется полное заполнение очереди. Другая модель системы характеризуется тем, что заявка на решение вычислительной задачи, поступившая в вычислительную систему, может ожидать и покидает ее только после полного обслуживания. В реальных вычислительных системах это оказывается возможным благодаря тому, что предусматриваются очереди O1-ОN. Так как очередь не может быть не ограниченной, то данная система характеризуется числом заявок, ожидающих начала обслуживания. Возможны дополнительные ограничения на время ожидания, на время пребывания заявки в вычислительной системе и др. Существенное влияние как на параметры обслуживающей системы, так и на процесс ее анализа оказывает характер входящего потока заявок. Заявки от ИВЗ образуют во времени поток, который может иметь ограниченное или неограниченное число задач. Различными могут быть и правила обслуживания заявок, находящихся в очереди. В соответствии с этим устанавливается некоторая дисциплина обслуживания диспетчером Д2. Естественной дисциплиной является дисциплина «первым пришел — первым обслужен». Возможен инверсный подход: «последним пришел — первым обслужен». Допускаются и случайные дисциплины обслуживания, когда заявки из очереди выбираются в произвольном порядке. В ряде случаев заявки обладают приоритетами. Это наиболее характерно для реальных задач ИС, в которых имеются информационные взаимосвязи. Тогда заявки имеют разную степень важности повремени исполнения и каждой заявке присваивается некоторый приоритетный индекс. Заявка с меньшим индексом имеет наибольший приоритет. Для приоритетного обслуживания различают дисциплины абсолютного, относительного и смешанного приоритетов, абсолютный предполагает прерывание обслуживания заявки при поступлении более приоритетной. При относительном приоритете обслуживание заявки продолжается, а после его завершения на обслуживание принимается поступившая приоритетная заявка, т. е. прерывание обслуживания не допускается. При смешанном приоритете ЭВМ выбирает либо новую заявку, либо продолжает обслуживание предыдущей заявки. Критерием выбора может служить время обслуживания заявки.
В теории массового обслуживания под временем обслуживания понимают время, которое затрачивается на обслуживание одной заявки конкретным обслуживающим прибором (ЭВМ). В общем случае время обслуживания характеризуется определенным законом распределения F(t)=P(to6c<t), где Р(to6c<t) — вероятность того, что время обслуживания to6c<t. При to6c≤0 F(t)=0. В зависимости от закона распределения заявки на решение вычислительные задачи могут быть разделены на типы. В рамках одного и того же закона распределения заявки можно различать по среднему времени обслуживания. Время обслуживания реальной заявки на ЭВМ определяется числом операций, входящих в программу. Существенное влияние на это время оказывает и разветвленность программы. Для слабо разветвленных программ число выполняемых операций практически для каждой задачи одинаково и может быть использована модель с постоянным временем обслуживания. При значительной разветвленной программы в зависимости от типа заявки ее реализация может пойти по разным направлениям, время выполнения программы будет случайной величиной, т. е. реализуется модель с переменным временем обслуживания. Поведение вычислительной системы во времени может быть описано на основе исследования марковского процесса. Тогда удается оценить характеристики системы массового обслуживания аналитическим путем.
Состояние системы массового обслуживания в некоторый момент времени t определяется числом находящихся в ней заявок N(t), где N(t) — это случайная величина, во времени N(t) отображает случайный процесс с дискретными состояниями. Положим, что система находится в состоянии k, если в ней имеется k заявок. Вероятность такого состояния обозначим Pk(t)=P[N(t)=k]. Для любого момента времени t При t2-t1=∆t и ∆t→0 Pij(∆t)»fij∆t, где Тогда
где N — максимальное число заявок в системе. Полагая t1=0, U=t, t2=t+t, t>0, получим
Можно составить систему таких уравнений для определенна вероятностей Рk(t). Процесс обработки может быть описан такими параметрами, как среднее время поступления и обслуживания заявок, характер распределения этих случайных величин относительно средних значений. Типовые варианты анализа системы могут быть получены для отдельных входных потоков заявок и определенных законов времени обслуживания в системе. В большинстве случаев анализ проводят для стационарного режима работы системы массового обслуживания, при котором вероятности нахождения системы в определенных состояниях не зависят от времени. Рассмотрим отдельные наиболее характерные модели обслуживания. Экспоненциальный закон времени обслуживания простейшего потока заявок. Простейшим называют стационарный ординарный поток без последействия. Обозначим параметр потока, т. е. интенсивность заявок, через l, l=const. Простейший поток описывается распределением Пуассона, в соответствии с которым вероятность возникновения k заявок за время t составляет
где l — интенсивность потока заявок, т. е. количество заявок, поступающих за единицу времени.
Среднее число заявок или математическое ожидание числа заявок за время t определяется как
Соответственно дисперсия числа заявок за время t
Особенностью простейшего потока является то, что при объединении независимых простейших потоков с параметрами l1, l2 возникает суммарный простейший поток с параметром (l1+l2). Это обстоятельство позволило широко применять простейший поток в прикладных исследованиях. Такая модель хорошо описывает многие потоки заявок вычислительных задач, которые возникают в реальных условиях эксплуатации. Экспоненциальному закону распределения времени обслуживания соответствует плотность распределения вероятности b(t)=me-mt, где m — интенсивность обслуживания;
Отсутствие заявок соответствует узлу 0, максимальное число заявок отображается узлом N. На дугах графа указаны плотности вероятности перехода системы из одного состояния в другое. При анализе процесса обработки необходимо установить вероятности состояний Рk(t), для этого необходимо составить N+1 линейных дифференциальных уравнений с постоянными коэффициентами. Структура уравнений одинакова: левая часть представляет собой производную вероятности состояния, а правая — включает члены, равные произведению плотности вероятности перехода на вероятность того состояния, из которого совершается переход. Число членов в правой части соответствует числу стрелок, входящих и исходящих из рассматриваемого состояния. Члены, соответствующие исходящим стрелкам, берутся со знаком минус, а соответствующие входящим — со знаком плюс. В общем виде уравнение, описывающее k -е состояние системы, может быть представлено как
В соответствии с рассмотренным графом для однолинейной системы обслуживания с очередью получаем следующую систему дифференциальных уравнений:
Условие нормировки вероятностей имеет вид Для стационарного режима рассмотренная система дифференциальных уравнений превращается в систему алгебраических уравнений вида:
Из полученной системы алгебраических уравнений нетрудно найти вероятность отсутствия заявок на решение вычислительных задач
Вероятность существования в системе k заявок, из которых одна обслуживается ЭВМ, а остальные находятся в очереди, составит
При k>N вероятность k -го состояния Рk=0. Это соответствует случаю переполнения системы, т. е. в очереди имеется N-1 заявок и одна заявка обслуживается ЭВМ (рис. 54). Таким образом, при полной загрузке системы, т. е. наличии в ней N заявок, вновь поступившее требование получает отказ. Поэтому полезно перейти к многолинейному обслуживанию, когда используется N обслуживающих приборов (ЭВМ).
Экспоненциальный закон времени обслуживания с потерями простейшего потока заявок при S обслуживающих приборах. В этом варианте вычислительная система не имеет возможности хранить очередь, поэтому заявки непосредственно через диспетчера Д2 поступают на одну из S ЭВМ. Число заявок не может превышать 5, поэтому в случае загрузки всех ЭВМ вновь поступающее требование теряется, так как очередь не предусмотрена, а на обслуживание оно не может быть принято. Граф переходов S обслуживающей системы представлен на рис. 55, где в узлах графа указаны состояния «0, 1,..., S» — по числу заявок в системе, а дуги размечены плотностями вероятностей переходов из одного состояния в другое.
Исходя из этого графа, для установившегося режима запишем алгебраическую систему уравнений в виде
Условие нормировки вероятностей имеет вид
При анализе процесса обработки весьма важно определить вероятность потери заявки на решение вычислительной задачи. Потеря заявки имеет место, если заявка поступает в вычислительную систему находящуюся в состоянии S,поэтому
Выражение для вероятности Рk известно в литературе как формула потерь Эрланга. Вероятность отсутствия заявок в системе
Отметим, что вероятность потери заявки может быть уменьшена за счет увеличения интенсивности обслуживания m и числа обслуживающих приборов S. Для любой системы весьма важным показателем является загрузка Экспоненциальный закон времени обслуживания простейшего потока заявок при S обслуживающих приборах. В этом варианте обслуживания вычислительная система включает S обслуживающих приборов (ЭВМ) и имеет очередь для поступающих заявок с числом мест L. При наличии хотя бы одной свободной ЭВМ поступившая заявка сразу принимается на обслуживание. Если все ЭВМ заняты, то она становится в очередь. Естественной дисциплиной обслуживания является «первым пришел — первым обслужен». По числу заявок система может иметь состояния: «0,1,.... S+L». Граф переходов системы представлен на рис. 56.
В узлах графа, как и ранее, указаны состояния, дуги графа размечены плотностями вероятностей переходов. На основании представленного графа запишем алгебраическую систему уравнений оценки вероятностей состояний системы для установившегося режима:
Условие нормировки вероятностей имеет вид
Решая систему уравнений, определим вероятность нахождения вычислительной системы в k -м состоянии
Соответственно вероятность состояния (S+n)
где вероятность отсутствия заявок в вычислительной системе
Отказ в приеме на обслуживание заявки возникает в случае, когда заняты все ЭВМ и в очереди находится L заявок, т. е.
Вероятность потерь из-за отказа в обслуживании уменьшается с увеличением длины очереди и особенно сильно с увеличением числа обслуживающих приборов. При
Организация очереди в вычислительной системе требует знания ее средней длины. Установим эту величину из условия, что очередь возникает, когда заняты все обслуживающие приборы и в системе имеет место количество заявок от S+1 до S+L. Поэтому
Подставляя соответствующие значения вероятностей Pk получим
При организации вычислительного процесса существенное значение имеет момент запуска и выпуска решаемой вычислительной задачи, поэтому весьма важно знать время пребывания заявки в очереди (время ожидания T ож). Потери в эффективности решения вычислительной задачи возникают в случае, когда время ожидания превышает заданное время t, следовательно, необходимо оценить вероятность того, что время ожидания в очереди будет больше некоторого фиксированного значения t. Тогда
В этом выражении первая сумма включает вероятности состояний обслуживающей системы от S до S+L, а вторая сумма — вероятности обслуживания от 0 до r заявок с помощью S обслуживающих приборов за время t. Среднее время ожидания
Для процесса обработки критическим может оказаться общее время пребывания заявки в вычислительной системе. Среднее значение времени пребывания требования в системе складывается из среднего значения времени ожидания и среднего значения времени обслуживания:
Из приведенных выше соотношений могут быть получены конечные выражения для однолинейной системы с ограниченной очередью. Подставляя S=1, находим
Потери заявок возникают с вероятностью
Соответственно среднее время пребывания заявки в вычислительной системе составит
Теория массового обслуживания позволяет получить аналитические выражения для оценки характеристик вычислительной системы при различных потоках заявок, отдельных законах обслуживания, наличии абсолютных и относительных приоритетов. Таким образом, модель обработки данных базируется на процессе обслуживания заявок по решению вычислительных задач. Модель обслуживания разрешается аналитическим либо имитационным методом на основе теории массового обслуживания. Однако для реальных задач управления необходимо решение вычислительных задач во временной последовательности, зависящей от требования производственного процесса. Стратегия обработки информации в автоматизированных системах должна исходить из того, что для каждой вычислительной задачи существует наиболее благоприятное время ее решения, что приводит к необходимости определения оптимального плана организации вычислительного процесса. Задача может в виде заявки обращаться в вычислительную систему в произвольный момент времени, однако возможности для ее решения должны определяться в соответствии с разработанным планом вычислительного процесса. Поэтому составной частью модели обработки данных является модель планирования вычислительных работ в системе.
2.5.2. Модели планирования вычислительного процесса
Для решения каждой задачи должен быть выделен определенный ресурс по объему оперативной и внешней памяти, по времени работы процессора, времени ввода-вывода информации. Естественно, что ограниченность вычислительных ресурсов может не позволить решать вычислительные задачи параллельно во времени. Учитывая, что вычислительная система при однолинейном обслуживании зачастую может решать только одну задачу, необходимо составить план последовательного запуска задач. Процесс назначения порядка решения задач во времени называется планированием. Для многолинейной системы планирование предполагает распределение заявок как во времени, так и в пространстве по используемым ЭВМ. В качестве распределяемых ресурсов выступают машинное время процессоров, объемы оперативной памяти и внешних запоминающих устройств, время работы устройств ввода-вывода. Эти ресурсы могут быть реализованы, если вычислительная задача подготовлена к выполнению ее вычислительной системой. Подготовка вычислительной задачи к исполнению осуществляется управляющей программой, называемой планировщиком. Планировщик обеспечивает ввод вычислительных задач в вычислительную систему с предварительным формированием определенных информационно-вычислительных работ на базе заявок вычислительных задач. При возникновении заявки на решение вычислительной задачи необходимо установить программу и набор данных, которые позволят сформировать информационно-вычислительную работу по решению данной задачи. Одновременно следует установить потребность в ресурсах и включить сформированную информационно-вычислительную работу в список работ, готовых для последующего исполнения. В результате планирования по каждой задаче может быть сформирован ряд работ, выполнение которых возможно при реализации управляющей программы, называемой супервизором. Супервизор обеспечивает предоставление каждой сформированной работе определенного ресурса процессора и других устройств вычислительной системы. Супервизор действует по запросу, на который откликается программа управления работами и процессором. При управлении информационно-вычислительными работами супервизор непрерывно инициируется командами, которые задает планировщик. Планировщик в соответствии с планом организации вычислительного процесса из множества заявок на решение вычислительных задач выделяет наиболее приоритетную и требует обеспечения ее соответствующими ресурсами. Для этого он обращается к программе управления вводом и выводом, памятью и т. д. В целом функция планирования реализуется управляющими программами планировщика и супервизора. Критерии, используемые при планировании вычислительного процесса, могут выбираться в зависимости от требований к решаемым вычислительным задачам. Можно идти по пути уменьшения среднего времени решения задач в вычислительной системе или увеличивать производительность. Возможны варианты, когда имеются ограничения на время решения конкретных задач, что особенно важно в системах управления в реальном масштабе времени. Рассмотрим модель планирования вычислительного процесса. Будем считать, что в целом для ряда вычислительных задач необходимым является выполнение определенной номенклатуры типовых вычислительных работ J1 — Jy, для которых необходимо предоставление ресурсов R1 — Rу. Связь между работами и ресурсами можно установить в виде матрицы трудоемкости работ. Элементами этой матрицы служат параметры tij, которые в зависимости от характера требуемого ресурса имеют размерность числа единиц потребной памяти либо единиц времени, необходимых для выполнения соответствующей работы. Тогда вводимая матрица имеет вид
Имея данную матрицу, при составлении плана организации вычислительного процесса необходимо указать очередность выполнения работы отдельными устройствами вычислительной системы, т. е. последовательность использования ресурсов R1 — Rν. Планирование вычислительного процесса осуществляется с целью составления последовательности, т. е. расписания выполнения информационно-вычислительных работ, производимых при решении поступивших вычислительных задач. Учитывая, что при решении вычислительной задачи используются разные устройства вычислительной системы (ВС), можно рассмотреть два крайних случая 1) порядок использования отдельных устройств ВС определяется поступившими вычислительными задачами; 2) порядок использования устройства ВС либо не известен, либо неодинаков для различных информационно-вычислительных работ. Этим крайним постановкам могут соответствовать и разные критерии эффективности составления плана вычислительных работ. Для первой постановки в качестве критерия может быть выбран минимум суммарного времени решения вычислительных задач, для второй — можно избрать в качестве критерия максимум загрузки устройств ВС. Планирование по минимуму суммарного времени решения вычислительных задач возможно, если известна матрица трудоемкостей отдельных работ. Предполагая, что ресурсы вычислительной системы используются последовательно, и, выделяя типовую последовательность прохождения любой вычислительной задачи, можно получить эффективный алгоритм планирования на основе задачи Джонсона, которая относится к теории расписаний и широко используется в календарном планировании. Планирование по критерию минимума времени обработки. При планировании вычислительного процесса необходимо учитывать следующие ограничения: 1) для любого устройства ВС (фазы обработки данных) каждая последующая работа не может начаться до окончания предыдущей; 2) каждое устройство на данной фазе может выполнять только одну информационно-вычислительную работу; 3) начавшаяся информационно-вычислительная работа не должна прерываться до полного ее завершения. Если в процессе обработки выделить g фаз, на каждой из которых используется одно вычислительное устройство, то решение данной задачи путем перебора требует рассмотрения (N!)g вариантов, где N — число заявок на решение вычислительных задач в вычислительной системе. Джонсоном получен эффективный алгоритм для g =2, требующий перебора N(N+1)/2 вариантов. Частное решение задачи Джонсона соответствует случаю g=l. По сути, это однолинейная система обслуживания (S=1), в которой имеется очередь заявок. Требуется установить порядок выборки этих заявок Диспетчером Д2 для обработки в ЭВМ. Критерием может быть минимум времени пребывания заявки в вычислительной системе, включая и время ожидания ее в очереди. Алгоритм выборки заявок из очереди по данному критерию соответствует их расположению в порядке убывания времени пребывания в вычислительной системе. Отметим, что решение задачи Джонсона при g=1 имеет слабое фактическое применение для вычислительной системы. Обычно при обработке данных используется более одного устройства. Отметим, что решение задачи Джонсона при g>2 означает практически сведение этой задачи к двухфазной. В частности, для g=3 получаем матрицу трудоемкостей, содержащую три столбца. Эту матрицу преобразуем в двухстолбцовую матрицу путем попарного сложения элементов трудоемкостей первого и второго, второго и третьего столбцов. Если ограничения, указанные Джонсоном, не выполняются, то точного решения задачи планирования вычислительного процесса не имеется, и переходят к эвристическим алгоритмам планирования информационно-вычислительных работ. В основе эвристических алгоритмов лежит выделение фазы работ с наибольшей суммарной продолжительностью. Данная фаза является приоритетной при запуске работ, которые располагаются в порядке убывания величин трудоемкостей их выполнения. Оценка эффективности эвристических методов планирования осуществляется по степени близости суммарного времени выполнения работ к минимально возможному времени. Планирование по критерию максимума загрузки средств обработки. Если последовательность использования вычислительных устройств в системе при решении задач неизвестна, то планирование ведут на основе критерия максимальной загрузки устройств. В этом случае из J1...Jg отбирается совокупность работ, которые могут выполняться совместно на базе имеющихся ресурсов. По мере окончания хотя бы одной работы из этой совокупности выполнения заеняется одной из работ, находящихся в ожидании. Для определения составов совокупностей работ преобразуем матрицу трудоемкостей в матрицу загрузки устройств. Введенные ранее ресурсы R1...Rg принадлежат некоторым устройствам У1...Уg. Тогда матрица загрузки может быть представлена в виде
где элемент матрицы Зij показывает загрузку j- гo устройства i- й работой; Тогда значение j определит номер потока, к которому будет отнесена работа, соответствующая данной строке матрицы. Число потоков будет равно числу устройств, т. е. g. Если в первой строке наибольшее значение имеет элемент З12, то работу J2, относим к потоку П2. Соответственно если во второй строке наибольшее значение имеет элемент З2g, то работу J2 относим к потоку Пg. При разбиении работ на потоки примем ограничение, что каждая из них может быть отнесена только к одному потоку. Каждый поток включает тогда некоторую последовательность работ. Сформировав g потоков, можно перейти к составлению совокупностей работ. Совокупности работ, поступающих на обработку, образуются путем выборки их из потоков П1...Пg. В начальный момент времени формируется первая совокупность, включающая g работ, взятых по одной из каждого потока. Эти работы поступают на соответствующие устройства при условии, что они не перегружают некоторый общий ресурс. В качестве такого ресурса может выступать емкость оперативной памяти, поэтому для каждого момента формирования совокупности работ должно соблюдаться ограничение: сумма емкостей памяти, занимаемых работами, включенными в совокупность, не должна превышать общей емкости памяти. Пусть в начальный момент совокупность работ имеет вид C1={J3, J1,…,J2}. Эта совокупность содержит g членов, из которых, как раньше приняли, работа J1 принадлежит потоку П2, а работа J2 прянадлежит потоку Пg. Ограничение по оперативной памяти примет вид V3+ V1 +... + Vi+... + V2≤ V, где V — общий объем оперативной памяти; Vi — объем оперативной памяти, необходимый для работы i. Если в некоторый момент времени завершается работа J1, то на ее место в совокупность работ включается следующая работа из того же потока П2. При этом опять проверяется ограничение. Если оно не соблюдается, то выбирается следующая работа из данного потока. При отсутствии работ, соответствующих ограничению, может быть выбрана новая из другого потока. Рассмотренные варианты планирования вычислительных работ при решении вычислительных задач являются классическими. Разработано большое число методов планирования, которые базируются на теории расписаний. Принципы планирования работ широко используются в типовых операционных системах современных ЭВМ.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.176.198 (0.017 с.) |

 . Переход из состояния i в состояние j опишем с помощью вероятности Pij(t1,t2), если в момент t1 система находилась в состоянии i, а к моменту t2 переходит в состояние j.
. Переход из состояния i в состояние j опишем с помощью вероятности Pij(t1,t2), если в момент t1 система находилась в состоянии i, а к моменту t2 переходит в состояние j.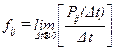 , где fij — плотность вероятности перехода. Рассмотрим последовательность переходов системы из состояния в состояние, пользуясь понятием Марковской цепи. Выберем интервал U в пределах t1<U<t2.
, где fij — плотность вероятности перехода. Рассмотрим последовательность переходов системы из состояния в состояние, пользуясь понятием Марковской цепи. Выберем интервал U в пределах t1<U<t2.
 .
. ,
, .
. .
. здесь Т обс — среднее время обслуживания одной заявки. Для составления уравнений, описывающих поведение системы массового обслуживания, рассмотрим граф переходов цепи Маркова для данной модели. На рис. 53 представлен размеченный граф состояний однолинейной системы обслуживания с очередью.
здесь Т обс — среднее время обслуживания одной заявки. Для составления уравнений, описывающих поведение системы массового обслуживания, рассмотрим граф переходов цепи Маркова для данной модели. На рис. 53 представлен размеченный граф состояний однолинейной системы обслуживания с очередью.

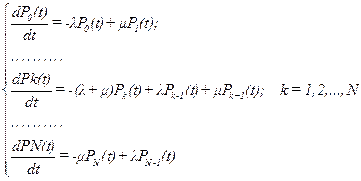 .
.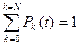
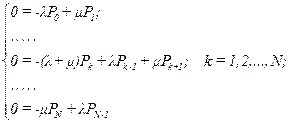 .
. .
. .
.


 . Решая данную систему уравнений, найдем вероятность пребывания вычислительной системы в k -м состоянии:
. Решая данную систему уравнений, найдем вероятность пребывания вычислительной системы в k -м состоянии: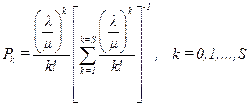
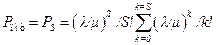 .
.
 , которая показывает среднее число заявок, поступающих в вычислительную систему за среднее время обслуживания одной заявки одной ЭВМ. Стационарный режим имеет место в системе, если r<S. Наиболее распространенным вариантом реализации вычислительной системы является многолинейное обслуживание с очередью, к рассмотрению которого и перейдем.
, которая показывает среднее число заявок, поступающих в вычислительную систему за среднее время обслуживания одной заявки одной ЭВМ. Стационарный режим имеет место в системе, если r<S. Наиболее распространенным вариантом реализации вычислительной системы является многолинейное обслуживание с очередью, к рассмотрению которого и перейдем.
 .
.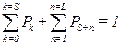
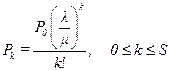 .
.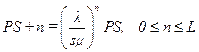 ,
, .
. .
. наблюдается уменьшение вероятности потерь на несколько порядков, с приближением
наблюдается уменьшение вероятности потерь на несколько порядков, с приближением  к единице это снижение становится менее существенным и находится в пределах одного порядка. Наличие очереди в системе позволяет снизить потери из-за отказа в обслуживании, но вызывает необходимость ожидания заявки в очереди перед началом обслуживания.
к единице это снижение становится менее существенным и находится в пределах одного порядка. Наличие очереди в системе позволяет снизить потери из-за отказа в обслуживании, но вызывает необходимость ожидания заявки в очереди перед началом обслуживания. .
. .
. .
.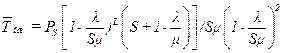 .
. .
.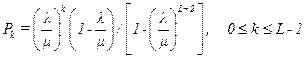 .
. .
.


 ;
;  — потребность i -й работы в использовании j -гo ресурса. В каждой строке матрицы выделим элемент Зij, с наибольшим значением.
— потребность i -й работы в использовании j -гo ресурса. В каждой строке матрицы выделим элемент Зij, с наибольшим значением.


