
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывно-стохастические модели (Q - схемы)Содержание книги
Поиск на нашем сайте
К ним относятся системы массовогообслуживания (англ. queuing system), которые называют Q- схемами. Теория массового обслуживания составляет один из разделов теории вероятностей. В этой теории рассматриваются вероятностные задачи и математические модели (до этого нами рассматривались детерминированные математические модели). Напомним, что: 1.Детерминированная математическая модельотражает поведение объекта (системы, процесса) с позиций полной определенности в настоящем и будущем. 2.Вероятностная математическая модель учитывает влияние случайных факторов на поведение объекта (системы, процесса) и, следовательно, оценивает будущее с позиций вероятности тех или иных событий. Т.е. здесь как, например, в теории игр задачи рассматриваются в условиях неопределенности. Рассмотрим сначала некоторые понятия, которые характеризуют «стохастическую неопределенность», когда неопределенные факторы, входящие в задачу, представляют собой случайные величины (или случайные функции), вероятностные характеристики которых либо известны, либо могут быть получены из опыта. Такую неопределенность называют еще «благоприятной». Понятие случайного процесса. Строго говоря, случайные возмущения присущи любому процессу. Проще привести примеры случайного, чем «неслучайного» процесса. Даже, например, процесс хода часов (вроде бы это строгая выверенная работа – «работает как часы») подвержен случайным изменениям (уход вперед, отставание, остановка). Но до тех пор, пока эти возмущения несущественны, мало влияют на интересующие нас параметры, мы можем ими пренебречь и рассматривать процесс как детерминированный, неслучайный. Пусть имеется некоторая система S (техническое устройство, группа таких устройств, технологическая система – станок, участок, цех, предприятие, отрасль промышленности и т.д.). В системе S протекает случайный процесс, если она с течением времени меняет свое состояние (переходит из одного состояния в другое), причем, заранее неизвестным случайным образом. Марковский случайный процесс. Случайный процесс, протекающий в системе, называется Марковским, если для любого момента времени t 0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t 0 и не зависят от того, когда и как система пришла в это состояние. Пусть в настоящий момент t0 система находится в определенном состоянии S 0. Мы знаем характеристики состояния системы в настоящем На практике Марковские процессы в чистом виде обычно не встречаются. Но имеются процессы, для которых влиянием «предистории» можно пренебречь. И при изучении таких процессов можно применять Марковские модели (в теории массового обслуживания рассматриваются и не Марковские системы массового обслуживания, но математический аппарат, их описывающий, гораздо сложнее). В исследовании операций большое значение имеют Марковские случайные процессы с дискретными состояниями и непрерывным временем. Марковские случайный процесс называется процессом с дискретным состоянием, если его возможные состояния S 1, S 2, … можно заранее определить, и переход системы из состояния в состояние происходит «скачком», практически мгновенно. Марковские случайный процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а неопределенны, случайны и могут произойти в любой момент. При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой – графом состояний. Вершины графа – состояния системы. Дуги графа – возможные переходы из состояния в состояние. Потоки событий. Поток событий – последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. В предыдущем примере – это поток отказов и поток восстановлений. Другие примеры: поток вызовов на телефонной станции, поток покупателей в магазине и т.д. Поток событий можно наглядно изобразить рядом точек на оси времени O t – рис. 7.
Рис.7. Изображение потока событий на оси времени Положение каждой точки случайно, и здесь изображена лишь какая-то одна реализация потока. Интенсивность потока событий ( Рассмотрим некоторые свойства (виды) потоков событий. Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность Поток событий называется потоком без последствий, если для любых двух непересекающихся участков времени Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу. Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: 1) стационарен; 2) ординарен; 3) не имеет последствий. Простейший поток имеет наиболее простое математическое описание. Он играет среди потоков такую же особую роль, как и закон нормального распределения среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему. Для простейшего потока с интенсивностью
где Для случайной величины T, имеющей показательное распределение, математическое ожидание
Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний. Рассматривая Марковские процессы с дискретными состояниями и непрерывным временем, подразумевается, что все переходы системы S из состояния в состояние происходят под действием простейших потоков событий (потоков вызовов, потоков отказов, потоков восстановлений и т.д.). Если все потоки событий, переводящие систему S из состояния в состояние простейшие, то процесс, протекающий в системе, будет Марковским. Итак, на систему, находящуюся в состоянии Для наглядности на графе состояний системы у каждой дуги проставляют интенсивности того потока событий, который переводит систему по данной дуге (стрелке). Пусть рассматриваемая система S имеет
Для нахождения всех вероятностей состояний Что будет происходить с вероятностями состояний при
где Финальные вероятности состояний – это уже не переменные величины (функции времени), а постоянные числа. Очевидно, что
Финальная вероятность состояния Например, система S имеет три состояния S 1, S 2 и S 3. Их финальные вероятности равны соответственно 0,2; 0,3 и 0,5. Это значит, что система в предельном стационарном состоянии в среднем 2/10 времени проводит в состоянии S 1, 3/10 – в состоянии S 2 и 5/10 – в состоянии S 3. Правило составления системы уравнений Колмогорова: в каждом уравнении системы в левой его части стоит финальная вероятность данного состояния Задачи теории массового обслуживания. Примеры систем массового обслуживания (СМО): телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, станочные и другие технологические системы, системы управления гибких производственных систем и т.д. Каждая СМО состоит из какого – то количества обслуживающих единиц, которые называются каналами обслуживания (это станки, транспортные тележки, роботы, линии связи, кассиры, продавцы и т.д.). Всякая СМО предназначена для обслуживания какого – то потока заявок (требований), поступающих в какие – то случайные моменты времени. Обслуживание заявки продолжается какое – то, вообще говоря, случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени обслуживания приводит к тому, что в какие – то периоды времени на входе СМО скапливается излишне большое количество заявок (они либо становятся в очередь, либо покидают СМО необслуженными). В другие же периоды СМО будет работать с недогрузкой или вообще простаивать. Процесс работы СМО – случайный процесс с дискретными состояниями и непрерывным временем. Состояние СМО меняется скачком в моменты появления каких - то событий (прихода новой заявки, окончания обслуживания, момента, когда заявка, которой надоело ждать, покидает очередь). Предмет теории массового обслуживания – построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками – показателями эффективности СМО. Эти показатели описывают способность СМО справляться с потоком заявок. Ими могут быть: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди; среднее время ожидания обслуживания и т.д. Математический анализ работы СМО очень облегчается, если процесс этой работы Марковский, т.е. потоки событий, переводящие систему из состояния в состояние – простейшие. Иначе математическое описание процесса очень усложняется и его редко удается довести до конкретных аналитических зависимостей. На практике не Марковские процессы с приближением приводятся к Марковским. Приведенный далее математический аппарат описывает Марковские процессы. Классификация систем массового обслуживания. Первое деление (по наличию очередей): 1. СМО с отказами. 2. СМО с очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем не обслуживается. В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной. СМО с очередями подразделяются на разные виды в зависимости от того, как организована очередь – ограничена или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания, «дисциплины обслуживания». Итак, например, рассматриваются следующие СМО: · СМО с нетерпеливыми заявками (длина очереди и время обслуживания ограничено); · СМО с обслуживанием с приоритетом, т.е. некоторые заявки обслуживаются вне очереди и т.д. Кроме этого СМО делятся на открытые СМО и замкнутые СМО. В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО – зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже исправно и ждет наладки. Классификация СМО далеко не ограничивается приведенными разновидностями, но этого достаточно. Математические модели простейших систем массового обслуживания. Ниже будут рассмотрены примеры простейших систем массового обслуживания (СМО). Понятие «простейшие» не означает «элементарные». Математические модели этих систем применимы и успешно используются в практических расчетах.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.236 (0.013 с.) |

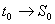 и все, что было при t < t 0 (предысторию процесса). Можем ли мы предугадать (предсказать) будущее, т.е. что будет при t > t 0? В точности – нет, но какие-то вероятностные характеристики процесса в будущем найти можно. Например, вероятность того, что через некоторое время
и все, что было при t < t 0 (предысторию процесса). Можем ли мы предугадать (предсказать) будущее, т.е. что будет при t > t 0? В точности – нет, но какие-то вероятностные характеристики процесса в будущем найти можно. Например, вероятность того, что через некоторое время 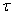 система S окажется в состоянии S 1 или останется в состоянии S 0 и т.д.
система S окажется в состоянии S 1 или останется в состоянии S 0 и т.д.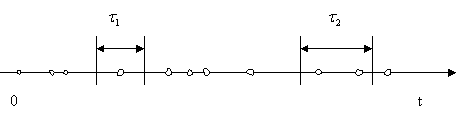
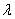 ) – это среднее число событий, приходящееся на единицу времени.
) – это среднее число событий, приходящееся на единицу времени.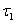 и
и 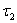 (см. рис.2) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами.
(см. рис.2) число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами.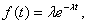
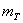 есть величина, обратная параметру, а среднее квадратичное отклонение
есть величина, обратная параметру, а среднее квадратичное отклонение 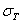 равно математическому ожиданию
равно математическому ожиданию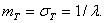
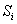 , действует простейший поток событий. Как только появится первое событие этого потока, происходит «перескок» системы из состояния
, действует простейший поток событий. Как только появится первое событие этого потока, происходит «перескок» системы из состояния 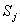 (на графе состояний по стрелке
(на графе состояний по стрелке 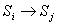 ).
).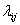 - интенсивность потока событий, переводящий систему из состояния
- интенсивность потока событий, переводящий систему из состояния 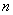 - возможных состояний
- возможных состояний 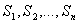 . Вероятность
. Вероятность 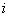 - го состояния
- го состояния 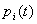 - это вероятность того, что в момент времени
- это вероятность того, что в момент времени 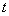 система будет находиться в состоянии
система будет находиться в состоянии 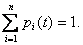
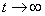 ? Будут ли
? Будут ли 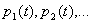 стремиться к каким-либо пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний:
стремиться к каким-либо пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний: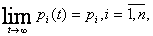
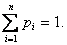
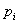 , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а в правой его части – сумма произведений интенсивностей всех потоков, входящих в
, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а в правой его части – сумма произведений интенсивностей всех потоков, входящих в 


