
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логическая модель представления знанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Значительное применение в теории искусственного интеллекта получила также логическая модель представления знаний. Знания, необходимые для решения, и решаемая задача описываются в этой модели определенными утверждениями на некотором логическом языке. Тогда знания составляют множество аксиом, а решаемая задача представляет собой доказываемую теорему. Процесс доказательства теоремы и составляет логическую модель представления знаний. Описание модели основывается на так называемой конструктивной логике. Значительную группу моделей представления знаний составляют процедурные модели. К этим моделям можно отнести языки логического Программирования (прологоподобные) языки, функциональные (лисп-подобные) языки, итеративные (алголоподобные) языки. Процесс формализации знаний хорошо прослеживается в методологии структурного программирования. В структурном программировавши нетрудно выделить языки, которые тождественны И-ИЛИ-структурам взаимосвязей отдельных подзадач. Для формализации знаний могут быть использованы и специальные модели их представления. Сюда можно отнести семантические сети, фрейм-сети, в которых используются графовые способы описания конструктивных процессов. При этом фрейм-сеть может быть рассмотрена как разновидность семантической сети и сводится к обычнному И-ИЛИ-графу. Рассмотрим, как наиболее общую, логическую модель представления знаний. Зададим логическую модель четверкой М=áТ, Р, A, Fñ, где Т— множество базовых элементов модели; Р — множество правил; А — множество истинных выражений (аксиом); F — правило вывода. Логическая модель может быть задана И-ИЛИ-графом, знажия в ней представляются множеством продукций на основе специальных символьных подстановок. В этой модели формулы интуиционистского исчисления высказываний связывают задачи как пропорциональные переменные: A ÇВ означает решить задачи А и В, AÈB означает решить хотя бы одну из этих задач, А→В означает свести решение А к решению В. Логическая модель описания задачи включает в себя язык, аксиомы, правила вывода. Прежде чем перейти к содержанию описания составляющих логической модели, определим концептуально понятие задачи. Будем считать, что задача включает в себя множество подзадач и взаимосвязей между ними. На нижнем уровне иерархии существует некоторая элементарная задача, для которой известна программа, выполняемая вычислительным средством без участия пользователя. Отсюда решение задачи есть нахождение правил, которые задают последовательность решения элементарных задач в зависимости от требуемого результата и исходных данных, имеющихся у пользователя. Исходные данные в нашей терминологии — это входные, а результаты решения задачи — это выходные данные. По существу, для задачи известными являются исходные данные и результаты решения совокупностей элементарных задач, входящих в состав данной задачи. В процессе решения необходимо получить значение выходных данных по значениям исходных данных, что осуществляется на основе выполнения программ их решений. Так как задачи пользователя являются не элементарными задачами, то это возможно путем поиска решений на базе использования логических моделей описания задач. На основе концептуального представления понятий «задача», «поиск решения» определим язык системы. Перечень символов системы составляет ее алфавит Т=Т1ÈТ2ÈТ3ÈТ4ÈТ5, где множество Т1 включает в себя имена задач и подзадач, т. е. T1 = {И1, И2,...,}; Т2 определяет структуру взаимосвязей подзадач, Т2={&, g}; T3 включает в себя символ сведения задачи к подзадачам, Тз={→}; Т4 включает вспомогательные символы, Т4={(,)}; Т5 включает символы истинности и ложности результатов решения задачи, Т5= {t,f}. На основе символов алфавита строятся формулы логической модели, т. е. множество правил Р. К правилам относят следующие: 1. Имя задачи есть ее описание. 2. Обозначим описание задач А, В, тогда А&В есть описание задачи, при котором необходимо решить задачу с описанием А и задачу с описанием В. AÈВ — это описание задачи, для решения которой достаточно решить задачу с описанием А либо задачу с описанием В. 3. Если описанием задачи является ее имя, то эта задача называется элементарной. Если задача с именем И сводится к задаче с описанием А, то И→А. При этом элементы описания А являются описаниями подзадач, входящих в задачу с именем И. 4. Символы 1, 0 означают описание задач с результатами их решения, символ 1 означает A=t, символ Æ означает A=f. Поиск решения задачи на основе логической модели представления знаний базируется на использовании ряда аксиом. Аксиома 1: AÈB=BÈA. Этой аксиомой определяется решение задачи, состоящей из двух подзадач: А, В. Исходная задача будет решена, если решена одна из этих подзадач. Таким образом, аксиома 1 утверждает, что подзадачи могут решаться в любой последовательности. Аксиома 2: (AÈB)ÈC=AÈ(BÈC). Эта аксиома формализует путь решения задачи, состоящей из трех подзадач: А, В, С. Исходная задача является решенной, если решена одна из этих подзадач. При этом любые две подзадачи могут быть объединены в одну подзадачу. Решение исходной задачи может состоять из решения одной из двух подзадач: имевшейся ранее и полученной в результате объединения. Последовательность решения подзадач может быть любой. Аксиома 3: (A&B)&C=A&(B&C). Данной схеме аксиомы соответствует исходная задача, включающая три подзадачи: А, В, С. Формула А & В определяет задачу, Решение которой может быть получено при условии, что решены подзадачи А, В. Учитывая, что в рассматриваемой схеме отсутствует символ логической связи задач, последовательность их решения может быть любой. Аксиома 4: А&(АÈВ)=А. Этой аксиомой определяется путь решения задачи, состоящей из подзадач А, В. Если подзадача А имеет решение, то имеет решение и подзадача А ÈВ. Если подзадача А решения не имеет, то исходная задача решения не имеет, так как А&(AÈВ)=Æ. Аксиома 5: АÈ(А&В)=А. Этой аксиомой отображается путь решения исходной задачи, включающей подзадачи А и В. Исходная задача может быть решена путем решения задача А или подзадач А и В совместно. Поскольку достаточно решить хотя бы задачу А, решение исходной задачи это и есть решение подзадачи А. Аксиома 6: (АÈВ)&С=А&СÈВ&С. Этой формуле соответствует исходная задача, включающая подзадачи А, В, С. Смысл аксиомы в том, что для получения решения исходной задачи достаточно решить одну из подзадач A ÈB совместно с решением задачи С. Аксиома 7: А&Æ0=Æ&.А =Æ. Эти аксиома отображает решение исходной задачи, включающей подзадачу А и подзадачу, обозначенную символом «Æ» Вторая подзадача решения не имеет. Так как исходная задача требует решения и первой, и второй подзадач, то и исходная задача решения не имеет. Аксиома 8: AÈÆ = A. Эта аксиома определяет путь решения исходной задачи, включающей в себя подзадачу А и подзадачу, которая решения не имеет. Поскольку для решения исходной задачи требуется решение одно из этих подзадач, необходимо решать ту подзадачу, которая имеет решение, так как решением исходной задачи будет решение подзадачи А. Аксиома 9: А&1 = 1&А=А. Формулой отображается исходная задача, включающая в себя две подзадачи: подзадачу А и подзадачу, отображаемую символом «1», т. е. подзадачу, решение которой уже получено. Эта подзадача является тривиальной. Учитывая, что решение исходной задачи включает в себя решение двух подзадач, одна из которых является тривиальной и имеет решение, то достаточно решить лишь задачу А. Аксиома 10: АÈ1 = 1. Эта аксиома отображает путь решения исходной задачи, включающей в себя подзадачу А и тривиальную подзадачу. Для решения исходной задачи необходимо иметь решение одной из этих подзадач, поэтому достаточно использовать решение тривиальной задачи. Приведенные аксиомы задают преобразования, позволяющие получать описание исходной задачи, эквивалентное заданному. Эти преобразования используются в процессе поиска решения исходной задачи. Путь получения решения задается правилами вывода (множеством F). Обобщенно они выражаются формулой Логической модели представления знаний и задач соответствует графическое отображение в виде графа редукции и графа пространства состояний. Вершины графа редукции соответствуют именам задач. Имя корневой вершины есть имя исходной задачи, имена дочерних вершин — это имена подзадач. Связи между подзадачами отображаются дугами, для конъюнкции используется гипердуга типа «И», для дизъюнкции — дуги типа «ИЛИ». По мере решений и перехода к последующим подзадачам осуществляется построение графа редукции сверху вниз. В концевых вершинах располагаются элементарные подзадачи, для которых существуют программы решения на ЭВМ. Поиск решения исходной задачи отображается на графе редукции последовательностью обхода его вершин. Граф редукции может быть преобразован в граф пространства состояний. Вершинами этого графа являются процессы решения элементарных подзадач либо процессы решения задач с ИЛИ-структурой взаимосвязей составляющих их подзадач. Вершины, определяющие элементарные подзадачи, имеют лишь одну исходящую дугу, а вершины, определяющие задачи с ИЛИ-структурой, имеют столько исходящих дуг, сколько данная задача содержит подзадач с ИЛИ-стружтурой. На этом графе должен существовать путь из корневой вершины в одну из концевых, что и задает получение решения задачи в виде последовательности обхода вершин графа пространства состояний. Следует отметить, что логическая модель представления задачи, граф редукции, граф пространства состояний являются эквивалентными представлениями процесса поиска решения исходной задачи. Реализация этой модели на ЭВМ с целью формализации знаний возможна на основе языка Пролог и ему подобных языков логического программирования.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.211 (0.007 с.) |

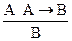 . Здесь предполагается, что исходная задача А сводится к задаче В, поэтому для решения задачи А необходимо решить задачу В. Последовательность описания решаемой задачи определяется правилами подстановки описаний составляющих ее подзадач. Смысл применения правил подстановки заключается в том, что для получения описания некоторой задачи необходимо дать описание последовательно составленных вложенных друг в друга подзадач с особым выделением элемента описания конечной подзадачи.
. Здесь предполагается, что исходная задача А сводится к задаче В, поэтому для решения задачи А необходимо решить задачу В. Последовательность описания решаемой задачи определяется правилами подстановки описаний составляющих ее подзадач. Смысл применения правил подстановки заключается в том, что для получения описания некоторой задачи необходимо дать описание последовательно составленных вложенных друг в друга подзадач с особым выделением элемента описания конечной подзадачи.


